Causal Reasoning from Meta-reinforcement Learning（自用笔记）

Abstract

• novel situations：元强化学习框架，agent 在新环境下能够有效
• The agent can select informative interventions , draw causal inferences from observational data, and make counterfactual predictions .
• 新的探索策略：structured exploration，providing agents with the ability to perform—and interpret—experiments.

Introduction

元学习对 从环境中学习 causal structure 的探索，《Recasting gradient-based meta-learning as hierarchical bayes》，论文摘要：元学习允许智能代理利用先前的学习情节作为快速提高新任务性能的基础。贝叶斯分层建模提供了一个理论框架，用于形式化元学习，作为对跨任务共享的一组参数的推断。在这里，我们重新定义了Finn等人的模型不可知元学习算法（MAML）。 （2017）作为分层贝叶斯模型中概率推断的方法。与通过分层贝叶斯进行元学习的现有方法相比，MAML通过使用可扩展的梯度下降过程进行后验推理，自然适用于复杂函数逼近器。此外，将MAML识别为分层贝叶斯提供了一种将算法作为元学习过程进行理解的方法，并提供了利用计算策略进行有效推理的机会。我们利用这次机会提出了对MAML算法的改进，该算法利用了来自近似推断和曲率估计的技术。

In our case, we train on a distribution of tasks that are each underpinned by a different causal structure. 不同任务的数据分布之间，形成一个因果结构。

We focus on abstract tasks that best isolate the question of interest: whether meta-learning can produce an agent capable of causal reasoning, when no notion of causality is explicitly given to the agent.

2 Problem Specification and Approach

三个 three distinct data settings ： observational （观察）、interventional （干预）、counterfactual（反事实）。

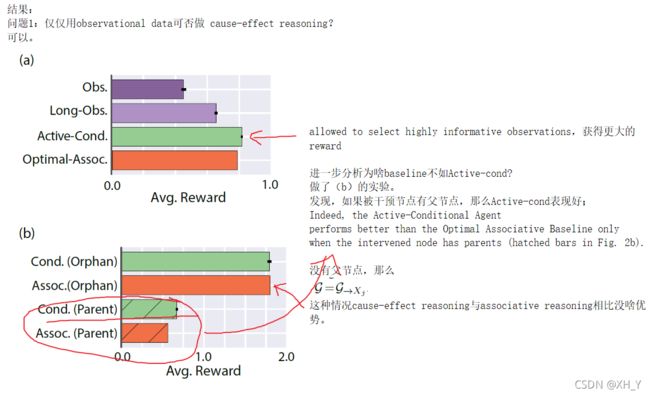
The observational setting (Experiment 1)：
agent 根据 observations 推理 correlations (associative reasoning) and, depending on the structure of the environment, causal effects (cause-effect reasoning).

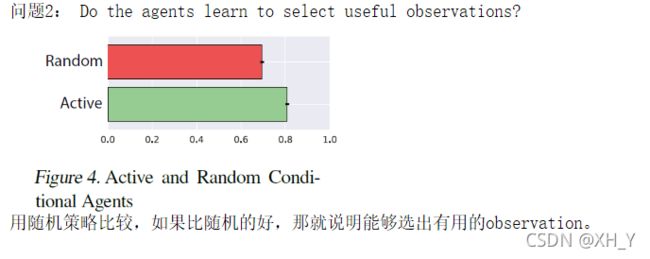
The interventional setting (Experiment 2):
setting the values of some variables and observing the consequences on other variables。可以设置 some variables 的值，并且观察other variables 的 结果。

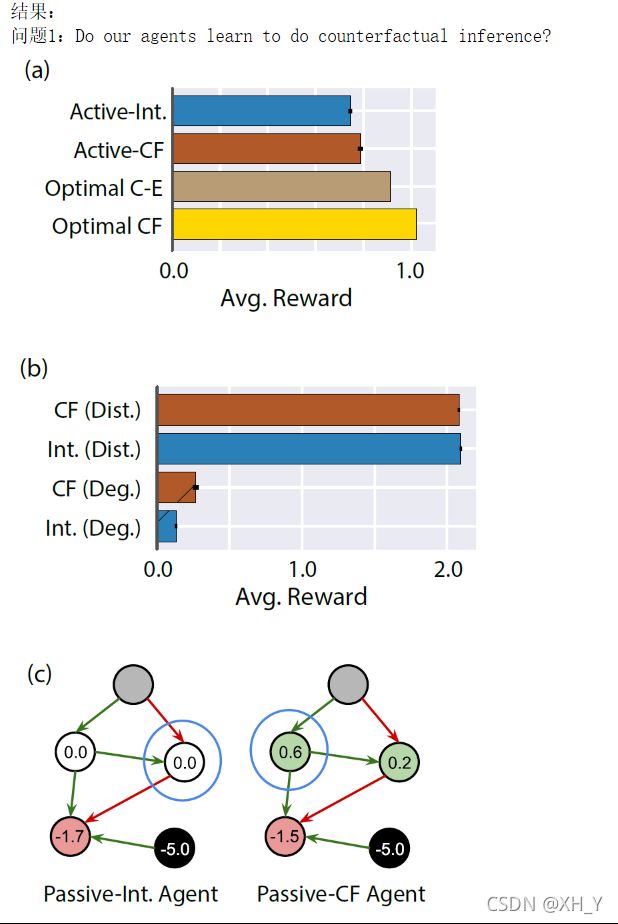
The counterfactual setting (Experiment 3):
可以通过 interventions 了解环境的 causal structure。在 episode 的最后一步，需要回答一个反事实问题 a counterfactual question of the form “What would have happened if a different intervention had been made in the previous timestep?”.

2.1. Causal Reasoning

随机变量之间的因果关系用 causal Bayesian networks (CBNs) 来表达。

CBN：有向无环图、节点 $X_i$ 表示一个随机变量、
联合分布 $p(X_1,...,x_N)$ 由 累乘计算得到：

Edges carry causal semantics : 有向路径 称为 causal paths。

上图 $X_i$ 到 $X_j$ 存在 a directed path，则 $X_i$ 是 $X_j$ 的 a potential cause 。 $X_i$ 在 $X_j$ 上的 causal effect 是给定 $X_i$ 后的 $X_j$ 的条件分布， restricted to only causal paths。

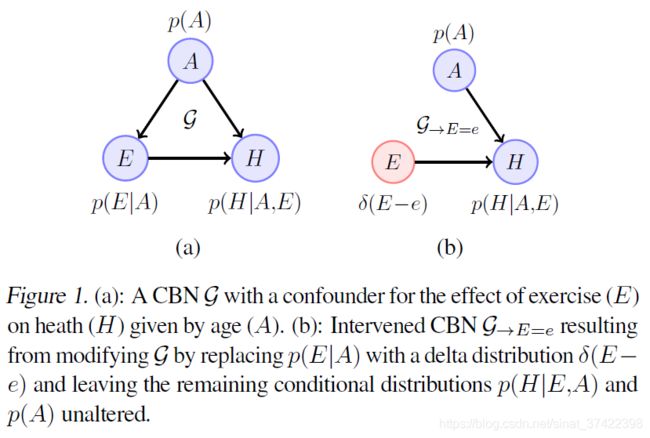
如 Fig. 1 （a）
$E$ 每周运动时长； $H$ 心脏健康； $A$ 年龄。
$E$ 对 $H$ 的 causal effect 是 the conditional distribution restricted to the path $E\to H$，不包括路径 $E\leftarrow A\to H$ 因为变量 $A$ 称为 confounder （混淆因子）

Cause-effect Reasoning
\quad 为计算 $E=e$的 causal effect， 将 $p(E|A)$ 用 a delta distribution $\delta (E-e)$ 代替， 则 $CBN{\mathcal{G}}_{\to E=e}$ 上的条件分布 $p_{\to E=e}(H|E=e)$ 表示 $E=e$的 causal effect （即为 移除 A 到 E 的边，是剩下条件分布 $p(H|E,A)$ 和 $p(A)$ ）

$p_{\to E=e}(H|E=e)$ 的计算 即为 do-calculus

\quad 如果我们知道图结构，知道混杂 A都有谁，那我们可以利用上述公式直接计算。但是存在不可观测的混杂时，唯一的计算 causal effect 的方法就是从被干预的图${\mathcal{G}}_{\to E=e}$ 中收集观察结果。例如，固定变量 $E=e$ 观察 ${\mathcal{G}}_{\to E=e}$ 中别的变量的结果。

Counterfactual Reasoning
\quad 上面的 Cause-effect reasoning 考虑到了 causal structure 和 confounding，可以回答预测问题 “Does exercising improve cardiac health?”

\quad 但是！不能回答 retrospective questions about what would have happened. 例如， 一个 individual $i$ 因为心脏病去世了，Cause-effect reasoning不能够回答“如果这个人做了更多的运动，他的健康状况会怎样？”这样的问题。

\quad 这种类型的问题需要对一个 a counterfactual world (that did not happen) 进行推理。为了做到这一点，我们可以首先使用来自 the observations from the factual world 和 knowledge about the CBN 来获得 an estimate of the specific latent randomness in the makeup of individual $i$ (for example information about this specific patient’s blood pressure and other variables as inferred by her having had a heart attack).
！！！ 也就是用 观测数据observations 和 CBN结构 来估计个体 $i$ 的 latent randomness （理解成 混淆因素）。（例如由她曾经有过心脏病发作而推断出她的血压和其他信息）。

然后，我们可以用这个估计值来计算运动干预下的心脏健康。这一程序在补充材料中作了更详细的解释。

2.2. Meta-learning

Learning the weights of the RNN by model-free RL ==》 “outer loop” of learning
The outer loop shapes the weights of the RNN into an “inner loop” learning algorithm. This inner loop algorithm plays out in the activation dynamics of the RNN and can continue learning even when the weights of the network are frozen.

a causally-aware inner-loop learning algorithm

“outer loop” = = 》梯度下降更新 RNN 参数 （个人理解：元学习框架下的外部循环，不同任务之间迭代更新RNN参数）
“inner loop” = = 》RNN输出 action （个人理解：RL框架下的内部循环，一个任务之内更新RNN参数）

3. Task Setup and Agent Architecture

1）数据 ：
节点数 N=5;
边：用上三角矩阵表示，weight从{-1,0,1}的均匀分布中采样。
这样总共生成 3^(N/(N-1)/2)=59049个 unique graphs。Graphs 被划分为等价类（结构相同，但节点标签的排列方式不同）。
测试集从所有graphs中随机选取12个图，再加上其等价类，共有408个graph。

node的取值 （就是environment部分是怎么给出各个node的值）：

• Parentless node: 从 $N(\mu =0.0,\theta =0.1)$ 中采样
• node $X_i$: Parents 是 $pa(X_i)$，从条件分布 $p(X_i|pa(X_i))=N(\mu ={\sum }_j{w}_{ji}{X}_j,\theta =0.1)$中采样，其中 $X_j\in pa(X_i)$
• A root node of $\mathcal{G}$ unobservable，即不可观测的混杂因素。图中一个根节点不可观测，Agent只能观测剩下4个。

2）Eposide ==》 agent 与一个不同的 CBN $\mathcal{G}$ 交互

• 如何选 $\mathcal{G}$ ？ 随机选取；under the constraints given in the next subsection.
• 分为两步：information phase；quiz phase

information phase
前 $T-1=4$ steps
allow the agent to collect information by interacting with or passively observing samples from $\mathcal{G}$

干预的情况 ：

• information action $a_t=i$ ==> 对 i-th node 进行干预 $X_{a_t}=X_i=5$ （为啥是5？作者说5这个值，在不进行干预的观察值的取值范围外。）
• 其余 nodes 的值 ==》 从 $p_{\to X_i=5}(X_{1:N/i}|X_i=5)$ 采样；

观察（不干预）的情况 ：

• action选择的是 quiz action。直接忽略这个action；$X_i$ 的 value $v_i$ 从 $\mathcal{G}$ 中采样；给予 $r_t=-10$的惩罚。在没有别的 reward，只有惩罚的reward。

quiz phase
第 $T=5$ step

随机选择一个 non-hidden node $X_j$ 进行干预 ==> value = -5（为啥取-5？防止agent直接记住 value=5的时候的result of intervations而不进行推理）
然后选择一个 node，这一步的reward就是选择的node $i$ 的值，$r_T=X_i=X_{a_T-(N-1)}$

如果选的是 information phase 阶段的动作，则给予$r_t=-10$的惩罚

如何随机选？–> 通过 $m_t$
$m_{T-1}=m_4$ 告知agent干预哪一个node；当$t<T-1=4$ 的时候 $m_t$ 是 zero vector。

经过这一阶段学习，agent可以得到CBN的$P(X_{1:N})$ 的信息，也就是学到了 CBN 的结构，可以做到关联性推理 （associative reasoning）$p(X_j|X_i=x)$

这一步为什么要增加变量 $m_t$ ? 而不是直接像是 information pahse 对nodes随机选择进行赋值就好？

2）强化学习框架：
Observation：$o_t=[v_t,m_t]$
\quad \quad \quad \quad \quad $v_t$ step $t$ 所有节点的值
\quad \quad \quad \quad \quad $m_t$ a one-hot vector indicating the external intervention during the quiz phase

Action: 动作空间是一个 长度为 $2(N-1)$ 的 vector，前 $N-1$ 针对 information phase，后 $N-1$ 针对 quiz phase。在两个 phases中，若选成了别的 phase的action，则忽略，并且给予惩罚。

Reward：如上分步phase所述。

4. Experiments

代码：kantneel/causal-metarl https://github.com/kantneel/causal-metarl
test_causal.py

def test_1():
    """Create a graph:
        4 -> 3 -> 1
          -> 2 -> 0
    - Test to see that mean observed values are correct
    """
    graph = CausalGraph(adj_list1)

    results = np.zeros(5)
    for i in range(10000):
        graph.intervene(4, 2)   # 将 node 4 干预为 2
        graph.intervene(2, 5)   # 将 node 2 干预为 5
        results += graph.sample_all()

    mean = results / 10000
    print(mean)

结果：

[ 1.9978613  -1.99858459  5.         -1.99836328  2.        ]

[-5.00009893 -2.000543    5.          1.99959025  2.        ]

[ 8.43961887e-04  1.06023776e-03  5.00000000e+00 -6.08591624e-04
  2.00000000e+00]

train.py也可以运行