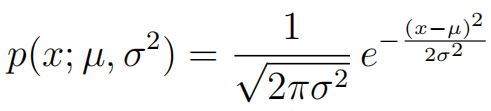机器学习编程作业ex8(matlab/octave实现)-吴恩达coursera 异常检测与推荐系统/协同过滤

程序打包网盘地址提取码1111

一、（Week 9）内容回顾

非监督学习问题的两种应用：异常检测与推荐系统

1.1 Anomaly Detection 异常检测

1.Density Estimation密度估计-用发生的概率来判定是否为异常数据
1)P(x)<ε,则为异常。可用于欺诈数据检测、制造数据检测-飞机引擎、计算机数据检测-运行不正常/停机

False positive代表：算法判定positives=1，判定错误false，实际为0。因此需要减少ε，提高判定为positives的要求，从而减少异常点（=1）。
2)高斯分布/正态分布Gaussian ：来自概率论中的概率分布函数，方差σ越小，越尖。
3)用高斯分布开发异常检测算法：p(x)的各个px_j为独立的元素，概率等于xi的乘积。如下图所示：

算法的三个过程：选特征、计算每个特征高斯分布的参数、计算概率。
2.建立异常检测算法系统：
1）评价异常算法：

• 对10000个好/20个坏数据的分类，好的按6:2:2，坏的按0、10、10，分成训练集、交叉验证集、测试集。
• 偏斜类问题用F score来评价-选用不同的ε，从中选用最低F的ε。

2)异常检测与监督学习的区别：

• 异常检测的y=1数据即异常数据占少量（如0~20个）；y=0则大量，监督学习则两个都很多。
• 实际问题选取模型的技巧：当异常样本少，异常的特征不能全部判定，需要用异常检测，即以概率ε来判定；监督学习用于正常、异常两个都有大量的样本数据，此时采用分类模型。
  垃圾邮件，异常样本很多，所以可用监督学习模型。

3）选择合适的特征建议：

• 首先用直方图绘制特征x与样本分布图，如果不符合高斯分布，用一些处理如取对数log、log（x+c）、根号x，使得x的特征分布变成高斯分布。
• 异常检测的误差分析：找到判断失误的正常样本，如下图中的划圈点，虽然出现概率大（靠近均值），仍属于异常样本，需要添加新的特征x2。
  
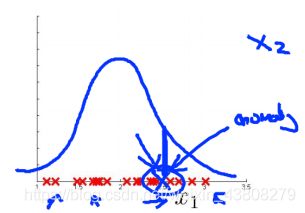
• 特征要选择适当-既不很大也不很小的特征；同时可以进行不同特征的组合，如x4/x5。

3.多元高斯分布
1）单元高斯分布表明特征之间相互独立，当存在相关性特征时，如下左图绿色点，应该为异常点，但若按单元高斯分布来做，会得出正常点的情况，此时，如下右图所示，x2的高斯分布对称性使得该点变到x2=0.3。因此，有相关性特征时要建立多元高斯分布。
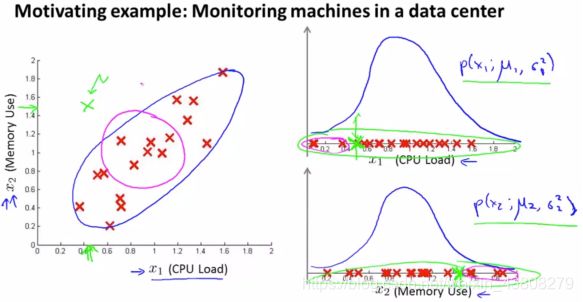两个变量的正相关、负相关：上图为正，因此协方差矩阵∑的副对角线为正值 。

2）多元高斯应用在异常检测-
核心依然为三个步骤（统计特征；求两个参数，均值μ和协方差矩阵∑；计算p并判定与e的关系）
多元高斯的协方差矩阵∑非对角线元素为0时，等同于是个单元高斯分布，即此时各个特征相互独立。

原始模型与多元高斯模型的比较：

• x1与x2有相关性，如CPU/内存，需用x1/x2单个特征手动代替x1、x2的两个特征，多元可以自动计算相关性；
• 原始模型计算量小，多元高斯计算量大，不适合n很大时；
• 原始模型的数据集数可以比较少，多元模型则一定要数据集数m大于特征数n，满足矩阵为奇异/可逆的条件，一般在m>10n时使用。

多元出现非奇异/矩阵不可逆情况时，从数据集数、特征重复-冗余特征/特征线性相关两个方面进行考虑。

第三个选项，识别是否为名人的头像，由于是与不是的样本都很多，因此可用监督学习的模型进行分类。

x1与x2相近时为正常数据，有一部分x1大、x2小的数据为异常数据，因此x1/x2可以确定异常数据为比值大、正常数据比值小。

1.2 Recommendation System 推荐系统

1.预测电影排序：

• 学习推荐系统的目的，是无监督学习的重要应用、可以自动学习特征
• 符号含义：nu用户user数量，nm电影movie数量，r(i,j)=1用户j给电影i评过分，y^r(r,j)只有在=1才有值（有意义）。

2.构建推荐系统的第一种方法-基于内容的推荐:线性回归

• 与之前的回归模型类似，求取参数向量θ代表对应x的权重，去预测评分
• 优化算法：最小化误差，采用梯度下降，得到θ1到θnu的一系列收敛值
  

3.第二种方法-不基于内容，协同过滤collaborative filtering。可以自行学习特征
初始化θ参数，去求x的值。再去算θ值，再去算x值。循环下去求得最佳的θ、x值

4.协同过滤算法改进:两个误差合并。
此时没有x0，原因为x为Rn，θ为Rn，X1可以收敛到=1，类似于x0=1。

这里的初始化x与θ，需要进行Symmetry breaking打破对称性-与之前神经网络参数的初始化类似，避免某些参数完全一样，浪费了计算时间。
5.协同过滤的向量化实现及应用 -low rank matrix factorization低秩矩阵分解
找到与i相关的j，确保两个xi与xj相近，向量化计算范数，可以确定特征相近的元素，用于推荐系统。
6.实施细节-均值归一化

• 进行均值归一化的目的：没看过电影的新用户，即没有x已知项，最终θ将全为0-最小化误差函数，θ必然=0
• 操作：每一行的和为0/均值为0。最终求得新用户的评分为μi，得到新用户的评分为平均值分值。
• 解决没用户比没评分/列要重要
  
• 不需进行特征缩放的原因，在于分值已经为同样的范围，而不是C选项的特征缩放原理-缩放后不影响参数求解
  
• 协同过滤算法特点是一部分数据，包括用户评分y、电影类型权重x，可以自动求得所有电影类型权重X和所有用户爱好向量θ。因此D选项为侧重于单人的数据，更推荐用分类算法，输出y=0、y=1对应喜欢/不喜欢。B选项很容易得到用线性回归模型，预测销售量。A、C都是基于已有的数据，去求得其中article文章的特征，找到特征向量差距小的相似文章。

需要编辑以下的红色文件。（后续部分，需要填入的代码为深色框，已经提供的代码为浅色框。）

文件	内容
ex8.m	异常检测主程序
ex8_cofi.m	协同过滤主程序
ex8data1.mat	异常检测数据集1
ex8data2.mat	异常检测数据集2
ex8_movies.mat	电影评论数据集
ex8_movieParams.mat	调试所需的参数
multivariateGaussian.m	计算高斯分布函数函数
visualizeFit.m	数据集和高斯分布的二维可视化函数
checkCostFunction.m	协同过滤的梯度检查函数
computeNumericalGradient.m	梯度计算函数
fmincg.m	最小化迭代函数
loadMovieList.m	加载电影数据集
movie_ids.txt	电影id清单
normalizeRatings.m	协同过滤的均值归一化
estimateGaussian.m	用协方差矩阵估计高斯分布的参数
selectThreshold.m	寻找异常检测的阈值ε
cofiCostFunc.m	协同过滤算法的代价函数

二、作业1- Anomaly detection 异常检测

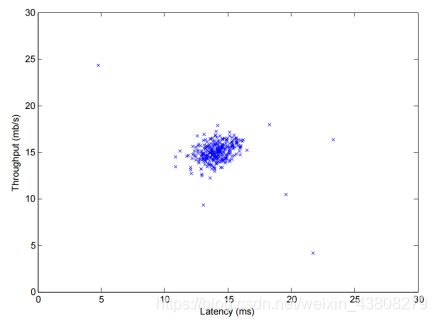
利用异常检测算法，检测服务器计算机中的异常行为（异常数据），特征包括服务器的吞吐量（mb/s）和响应延迟（s），应用模型为无监督学习-数据无标签。

2.1 Part 1: Load Example Dataset 加载样本数据集

load(‘ex8data1.mat’);
plot(X(:, 1), X(:, 2), ‘bx’);
axis([0 30 0 30]);
xlabel(‘Latency (ms)’);
ylabel(‘Throughput (mb/s)’);

得到数据如下所示，共有307个数据点：

2.2 Part 2: Estimate the dataset statistics 数据集统计估计

[mu sigma2] = estimateGaussian(X);
p = multivariateGaussian(X, mu, sigma2);
visualizeFit(X, mu, sigma2);
xlabel(‘Latency (ms)’);
ylabel(‘Throughput (mb/s)’);

主函数提供高斯分布参数estimateGaussian计算的函数入口，X为307*2的矩阵，函数计算得到两列的两个均值μ、两个方差σ。

function [mu sigma2] = estimateGaussian(X)
[m, n] = size(X);
mu = zeros(n, 1);
sigma2 = zeros(n, 1);
  % YOUR CODE HERE
end

因此，需要在estimateGaussian.m文件中填入代码：

mu = 1/m*(sum(X));
sigma2 = 1/m*sum((X-mu).^2);

multivariateGaussian由均值和方差可以得到高斯分布函数p，最终得到307*1列向量的p。

function p = multivariateGaussian(X, mu, Sigma2)
k = length(mu);
if (size(Sigma2, 2) == 1) || (size(Sigma2, 1) = = 1)
Sigma2 = diag(Sigma2);   %diag函数将σ的行向量元素扩展为矩阵的对角线元素，其他元素均为0
end
X = bsxfun(@minus, X, mu(: )’);   %bsxfun函数为隐式扩展运算
  %如这里X每个元素都减去均值行向量mu的值（mu由1*2变成307 *2）
p = (2 * pi) ^ (- k / 2) * det(Sigma2) ^ (-0.5) * …
exp(-0.5 * sum(bsxfun(@times, X * pinv(Sigma2), X), 2));
end

visualizeFit由数据集、均值、方差，绘制高斯分布概率值p的等高线图和数据分布图

function visualizeFit(X, mu, sigma2)
[X1,X2] = meshgrid(0:.5:35);  %设定二维坐标点，meshgrid得到71*71个坐标点
Z = multivariateGaussian([X1(: ) X2(: )],mu,sigma2);
Z = reshape(Z,size(X1));
plot(X(:, 1), X(:, 2),‘bx’);  %绘制数据点
hold on;
% Do not plot if there are infinities
if (sum(isinf(Z)) == 0)   %isinf（Z）返回Z中为无限值Inf的元素
contour(X1, X2, Z, 10.^ (-20:3:0)’);  %绘制高斯分布函数值为10 ^-20、10 ^-17……10 ^-2的二维等高线图
end
hold off;
end

2.3 Part 3: Find Outliers 确定概率阈值ε

主函数利用交叉验证集选择F score最小的概率阈值ε，首先计算验证集的分布函数pval

pval = multivariateGaussian(Xval, mu, sigma2);
[epsilon F1] = selectThreshold(yval, pval); %获得最佳的ε
fprintf(‘Best epsilon found using cross-validation: %e\n’, epsilon);
fprintf(‘Best F1 on Cross Validation Set: %f\n’, F1);
fprintf(’ (you should see a value epsilon of about 8.99e-05)\n’);
fprintf(’ (you should see a Best F1 value of 0.875000)\n\n’);
% Find the outliers in the training set and plot the
outliers = find(p < epsilon); %找到概率小于阈值ε的异常点，将序号存储在outliers中
% Draw a red circle around those outliers
hold on
plot(X(outliers, 1), X(outliers, 2), ‘ro’, ‘LineWidth’, 2, ‘MarkerSize’, 10); %获取异常点的x、y坐标并绘图
hold off

selectThreshold由yval和pval计算不同ε下的F score，得到最低情况下的ε。

function [bestEpsilon bestF1] = selectThreshold(yval, pval)
bestEpsilon = 0;
bestF1 = 0;
F1 = 0;
stepsize = (max(pval) - min(pval)) / 1000;
for epsilon = min(pval):stepsize:max(pval) %计算1000个ε的不同F1值
  %YOUR CODE HERE
  if F1 > bestF1
  bestF1 = F1;
  bestEpsilon = epsilon;
  end
end
end

因此，需要在selectThreshold.m中填入代码：

 cvPredictions=(pval<epsilon);
    tp = sum((cvPredictions == 1) & (yval == 1));
    fp = sum((cvPredictions == 1) & (yval == 0));
    fn = sum((cvPredictions == 0) & (yval == 1));
    prec = tp / (tp + fp);
    rec = tp / (tp + fn);
    F1 = 2*prec*rec/(prec+rec);

F1值的计算公式如下所示，其中：（算法判定为y=1，代表为异常数据）

• tp为true positives，算法判定positives=1，判定正确true，实际也为1。
• fp为false positives，算法判定positives=1，判定错误false，实际为0。
• fn为false negatives，算法判定negatives=0，判定错误false，实际为1。
  

2.4 Part 4: Multidimensional Outliers 多特征时的最佳阈值

load(‘ex8data2.mat’);
[mu sigma2] = estimateGaussian(X);  %计算数据集的方差、均值
p = multivariateGaussian(X, mu, sigma2);  %计算训练集的高斯分布函数
pval = multivariateGaussian(Xval, mu, sigma2);  %计算交叉验证集的高斯分布函数
[epsilon F1] = selectThreshold(yval, pval);  %得到最佳的epsilon参数
fprintf(‘Best epsilon found using cross-validation: %e\n’, epsilon);
fprintf(‘Best F1 on Cross Validation Set: %f\n’, F1);
fprintf(’ (you should see a value epsilon of about 1.38e-18)\n’);
fprintf(’ (you should see a Best F1 value of 0.615385)\n’);
fprintf(’# Outliers found: %d\n\n’, sum(p < epsilon));

三、作业2-Recommender Systems 推荐系统

利用协同过滤算法，估计用户的电影评分，由此来推荐类似的高分电影。用户数nu=943，电影数nm=1682。

3.1 Part 1: Loading movie ratings dataset 加载电影评分数据库

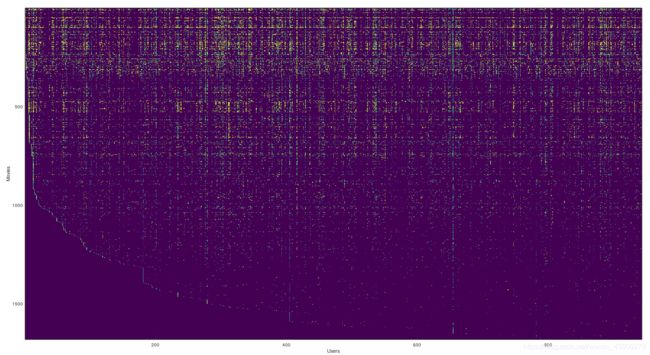
主函数加载了数据文件，Y为1682*943矩阵，代表943个用户给1682个电影打的分。

load (‘ex8_movies.mat’);
fprintf(‘Average rating for movie 1 (Toy Story): %f / 5\n\n’, …
mean(Y(1, R(1, )));
imagesc(Y);  %imagesc将矩阵数据转换为二维图
ylabel(‘Movies’);
xlabel(‘Users’);

如下图所示：

3.2 Part 2代价函数、Part 3 梯度检验、Part 4/5 回归项

load (‘ex8_movieParams.mat’);
num_users = 4; num_movies = 5; num_features = 3;
X = X(1:num_movies, 1:num_features);
Theta = Theta(1:num_users, 1:num_features);
Y = Y(1:num_movies, 1:num_users);
R = R(1:num_movies, 1:num_users);
J = cofiCostFunc([X( ; Theta(], Y, R, num_users, num_movies, …
num_features, 0);
fprintf(['Cost at loaded parameters: %f '…
‘\n(this value should be about 22.22)\n’], J);

cofiCostFunc函数根据评分数据和参数，计算此时的代价。这里直接加入回归项：


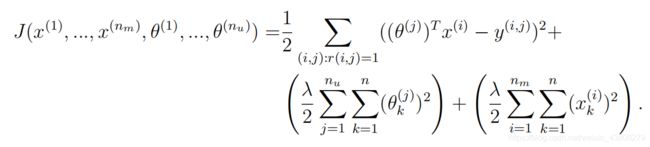
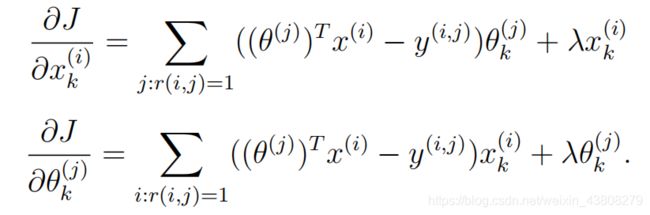
因此，在cofiCostFunc.m文件中填入代码：

predY = (X*Theta') .* R;
J = 1/2*sum(sum((predY-Y) .^ 2)) +...
    lambda/2*sum(sum(Theta .^ 2))+...
    lambda/2*sum(sum(X .^ 2));;

for i=1:num_movies
    idx=find(R(i,:)==1);
    Theta_temp=Theta(idx,:);
    Y_temp=Y(i,idx);
    X_grad(i,:)=(X(i,:)*Theta_temp'-Y_temp)*Theta_temp+...
        lambda*X(i,:);
end

for i=1:num_users
    idx=find(R(:,i)==1);
    X_temp=X(idx,:);
    Y_temp=Y(idx,i);
    Theta_grad(i,:)=(X_temp*Theta(i,:)'-Y_temp)'*X_temp+...
        lambda*Theta(i,:); 
end

3.6 Part 6: Entering ratings for a new user 对用户进行电影推荐

主函数为输入某个用户已评分的电影，存储在my_ratings中。

movieList = loadMovieList();
% Initialize my ratings
my_ratings = zeros(1682, 1);
% Check the file movie_idx.txt for id of each movie in our dataset
% For example, Toy Story (1995) has ID 1, so to rate it “4”, you can set
my_ratings(1) = 4;
% Or suppose did not enjoy Silence of the Lambs (1991), you can set
my_ratings(98) = 2;
% We have selected a few movies we liked / did not like and the ratings we
% gave are as follows:
my_ratings(7) = 3;
my_ratings(12)= 5;
my_ratings(54) = 4;
my_ratings(64)= 5;
my_ratings(66)= 3;
my_ratings(69) = 5;
my_ratings(183) = 4;
my_ratings(226) = 5;
my_ratings(355)= 5;
fprintf(’\n\nNew user ratings:\n’);
for i = 1:length(my_ratings)
if my_ratings(i) > 0
fprintf(‘Rated %d for %s\n’, my_ratings(i), …
movieList{i});
end
end

3.7 Part 7: Learning Movie Ratings 计算电影排名

load(‘ex8_movies.mat’);
% 加入用户的已知评分数据
Y = [my_ratings Y];
R = [(my_ratings ~= 0) R];
% 均值归一化
[Ynorm, Ymean] = normalizeRatings(Y, R);
% Useful Values
num_users = size(Y, 2);
num_movies = size(Y, 1);
num_features = 10;
% 设初始值 (Theta, X)
X = randn(num_movies, num_features);
Theta = randn(num_users, num_features);
initial_parameters = [X(: ); Theta(: )];
% 迭代参数设置
options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, 100);
% 迭代获得最佳的Theta和X参数
lambda = 10;
theta = fmincg (@(t)(cofiCostFunc(t, Ynorm, R, num_users, num_movies, …
num_features, lambda)), …
initial_parameters, options);
% 还原参数
X = reshape(theta(1:num_moviesnum_features), num_movies, num_features);
Theta = reshape(theta(num_moviesnum_features+1:end), …
num_users, num_features);
fprintf(‘Recommender system learning completed.\n’);

3.8 Part 8: Recommendation for you

p = X * Theta’;
my_predictions = p(:,1) + Ymean;
movieList = loadMovieList();
[r, ix] = sort(my_predictions, ‘descend’);  %根据电影id，计算并排序相应的评分
fprintf(’\nTop recommendations for you:\n’);
for i=1:10  %推荐前10部评分最高的电影
j = ix(i);
fprintf(‘Predicting rating %.1f for movie %s\n’, my_predictions(j), …
movieList{j});
end
fprintf(’\n\nOriginal ratings provided:\n’);
for i = 1:length(my_ratings)
if my_ratings(i) > 0
fprintf(‘Rated %d for %s\n’, my_ratings(i), …
movieList{i});
end
end

参考资料

吴恩达机器学习Coursera-week9
吴恩达机器学习编程作业ex8-Matlab版