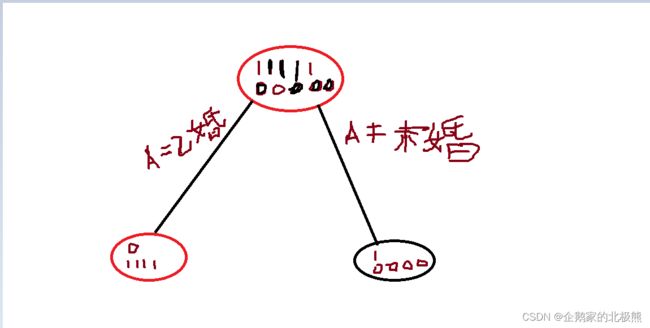
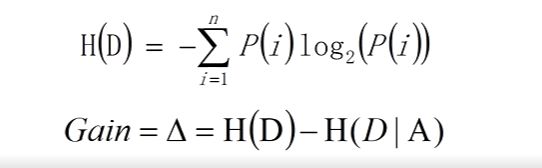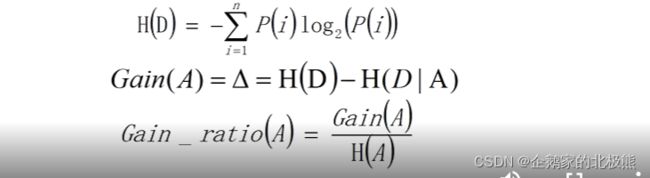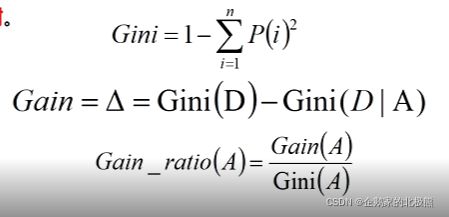- Protein FID:AI蛋白质结构生成模型评估新指标
一、引言:蛋白质生成模型面临的评估挑战近年来,AI驱动的蛋白质结构生成模型取得了令人瞩目的进展,但如何有效评估这些模型的质量却一直是一个悬而未决的问题。虽然实验验证仍然是金标准,但计算机模拟评估对于快速开发和比较机器学习模型至关重要。然而,尽管最先进的模型在当前评估指标上表现卓越,但它们在实际设计应用中的成功率仍然相对有限。例如,有研究报告显示生成结构的实验成功率仅为3%,而计算机模拟评分却远高于
- 0315_算法22级1班实验2(递归分治策略)
目录ProblemA众数问题题目描述输入输出样例输入样例输出思路分析代码实现思路优化ProblemB半数集问题题目描述输入输出样例输入样例输出思路分析代码实现ProblemC查找数组拐点题目描述输入输出样例输入样例输出思路分析代码实现思路优化ProblemA众数问题题目描述所谓众数,就是对于给定的含有N个元素的多重集合,每个元素在S中出现次数最多的成为该元素的重数,多重集合S重的重数最大的元素成为
- 0301_算法22级1班实验1
目录ProblemA统计数字问题1.题目描述2.思路分析3.代码实现ProblemB字典序问题1.题目描述2.思路分析3.代码实现ProblemC最多约数问题1.题目描述2.思路分析3.代码实现ProblemA统计数字问题1.题目描述题目描述问题描述:一本书的页码从自然数1开始顺序编码直到自然数n。书的页码按照通常的习惯编排,每个页码都不含多余的前导数字0。例如,第6页用数字6表示,而不是06或0
- 在 Conda 中删除环境及所有安装的库
Studying 开龙wu
conda
注意事项1.删除环境前确保你没有在该环境中运行任何程序。2.删除操作是不可逆的,所有该环境中的包和配置都会被永久删除。3.如果你想保留环境的配置信息,可以在删除前使用condaenvexport>environment.yml导出环境配置。关于requirements.txt和environment.yaml文件使用介绍详情可参考以往文章,争对机器学习和深度学习里Python项目开发管理项目依赖的
- OpenCV中常用特征提取算法(SURF、ORB、SIFT和AKAZE)用法示例(C++和Python)
点云SLAM
图形图像处理opencv算法ORB算法SIFT算法SURF算法AKAZE算法计算机视觉
OpenCV中提供了多种常用的特征提取算法,广泛应用于图像匹配、拼接、SLAM、物体识别等任务。以下是OpenCV中几个主流特征提取算法的用法总结与代码示例,涵盖C++和Python两个版本。常用特征提取算法列表算法特点是否需额外模块SIFT(尺度不变特征)稳定性强、可旋转缩放xfeatures2d模块SURF(加速稳健特征)快速但专利保护xfeatures2d模块ORB(OrientedFAST
- 【AI 赋能:Python 人工智能应用实战】5. 梯度下降家族:SGD/Adam优化器对比实验与选择策略
AI_DL_CODE
人工智能python梯度下降优化器SGDAdamPyTorch
摘要:本文系统解析梯度下降优化器的核心原理与演进脉络,构建从理论到实战的完整知识体系。理论部分梳理优化器发展里程碑,从1951年的SGD到2018年的AdamW,揭示技术迭代逻辑;通过数学公式对比SGD、Momentum、Adam等核心算法的更新机制,解析动量加速、自适应学习率的创新点。结合损失曲面分析,阐释Momentum如何逃离鞍点、Adam如何处理悬崖梯度。实战模块基于PyTorch在MNI
- 脱岗离岗逃岗监测识别软件系统平台 标检测算法#YOLO
值班脱岗智能监测识别系统是一种利用AI视频智能分析技术的智能化系统,能够对办公工作岗位区域、岗亭、值班室、生产线岗位等进行7*24小时不间断实时监测。该系统的出现,有助于提高工作效率,确保工作秩序的正常运行,同时也能有效避免值班人员脱岗、懈怠等现象的发生。该系统的工作原理是通过高清摄像头捕捉实时画面,然后利用AI视频智能分析技术对画面进行实时分析,识别出是否有人脱岗、懈怠或者有其他异常情况发生。当
- 颠覆未来:创新代码引领人工智能与量子计算深度融合
金枝玉叶9
程序员知识储备1程序员知识储备2程序员知识储备3人工智能量子计算
摘要在信息时代飞速演进的背景下,人工智能与量子计算正以前所未有的速度互相融合,推动着科技边界的不断拓展。本文回顾了经典算法的智慧,展示了前沿深度学习模型的构建,并通过量子电路设计探讨了创新代码的可能性,为探索未来科技变革提供了全新视角。1.引言当前,科技创新正处于高速迭代的关键阶段,传统计算方法与新型技术的交汇处正成为研究热点。人工智能的发展已渗透到各行各业,而量子计算的崛起则为解决复杂计算问题提
- 智界R7智驾功能和性能评价
TheWanderers
智能驾驶智界
一、智驾行车能力标题硬件配置与系统架构感知硬件:Max/Ultra版搭载1个192线激光雷达、3个毫米波雷达(含1个4D成像雷达)、12个超声波雷达、11个高清摄像头(含前向800万像素双目+鱼眼镜头)。Pro版未配备激光雷达,但保留3个毫米波雷达和10个摄像头。核心算法:HUAWEIADS3.0系统,基于端到端架构,整合感知、决策与控制模块,支持全场景目标识别(如非标准障碍物、夜间行人)。算力支
- 人工智能视频分析系统人员离岗报警设计方案
liuhu21
人工智能云计算运维
一、方案概述近几年安防监控技术不断的进步,特别是在人工智能推出之后。安防监控系统结合人工智能算法做到了许多以前无法做到的事情。就比如我们今天要说的离岗检测报警监控系统。以前我们只能通过人工值守监控室的方式,通过人的判断去观看现场人员在岗情况。如今有了离岗检测监控系统,系统可以自动监测现场人员是否在岗、离岗时间以及离岗人数等等。这样,大大减少了监控室值班人员的工作量,同时相较人工监管提升了工作效率。
- 睡岗离岗检测算法 Python
燧机科技SuiJi
人工智能python算法深度学习神经网络
睡岗离岗检测算法的核心在于实时监控和智能分析,睡岗离岗检测算法通过安装在关键区域的监控摄像头,系统能够捕捉到员工的活动画面。当系统检测到人体位置长时间未发生变化时,将启动睡姿分类器。该分类器能够识别多种睡姿,如趴在桌子上睡、坐在凳子上后仰睡等。一旦识别为睡姿,系统将立即触发告警机制。这可以通过向管理人员发送警报信号,或通过语音提醒员工的方式实现。睡岗离岗检测算法在多种场景下均有广泛应用。该算法能够
- 微算法科技技术创新,将量子图像LSQb算法与量子加密技术相结合,构建更加安全的量子信息隐藏和传输系统
随着信息技术的发展,数据的安全性变得尤为重要。在传统计算模式下,即便采用复杂的加密算法,也难以完全抵御日益增长的网络攻击威胁。量子计算技术的出现为信息安全带来了新的解决方案。然而,量子图像处理领域仍面临复杂度高、效率低的问题。微算法科技通过将量子图像LSQb算法与量子加密技术相结合,提出了一种全新的信息隐藏和传输方案,旨在构建更加安全高效的数据保护机制。LSQb算法,即量子图像的最小有效量子比特算
- 5万人流挤地铁如何追踪?陌讯算法实战FPS飙升300%
开篇痛点在智慧城市安防场景中,传统视觉算法常面临“三难困境”:低光照漏检率飙升(夜间误报率超30%)、人群遮挡ID切换混乱(MOTA指标<50%)、硬件资源吃紧(1080P视频流处理>200ms)。某省会交警平台曾反馈:“雨雾天车牌识别准确率骤降至65%,追踪目标平均5分钟丢失1次”。技术解析:动态多目标蒸馏网络陌讯视觉算法创新性融合多任务蒸馏架构与时空注意力机制,攻克复杂场景泛化难题。核心公式创
- 3步实现安防高精度检测:陌讯算法夜间监控落地实战
2501_92474745
目标跟踪人工智能计算机视觉算法目标检测视觉检测
开篇痛点:安防监控系统在实时目标检测中常面临严峻挑战。实测数据显示,传统算法在低光、遮挡或动态场景下,泛化能力不足,导致平均误报率高达15%(数据来源:安防行业报告)。尤其在夜间或拥挤环境下,系统卡顿、漏检频发,不仅降低响应效率,还增加安全隐患。例如,某城市交通监控中心反馈,其开源模型在高密度人流中出现每秒帧率(FPS)骤降至20帧以下,引发报警延迟问题。这些问题根源在于算法鲁棒性和实时性不足,亟
- 离岗误报率 20%?陌讯时序算法实测降 90%
2501_92474711
算法计算机视觉目标跟踪机器学习人工智能边缘计算
开篇:工业安防中的"隐形漏洞"在制造业车间、变电站等关键场景,离岗检测是保障生产安全的核心环节。传统监控系统依赖人工巡检,存在85%的漏检率;而普通视觉算法在光照变化、人员遮挡场景下,误报率常高达20%以上[实测数据显示]。某汽车零部件厂曾因离岗检测失效导致设备空转2小时,直接损失超12万元。这种"看得见的监控,防不住的风险"困境,凸显了传统视觉方案在复杂工业场景中的局限性。技术解析:从单帧检测到
- 雨天障碍物漏检?陌讯多模态算法实测 98% 准确率
2501_92474711
算法目标跟踪人工智能计算机视觉
开篇痛点:自动驾驶视觉系统的“暗礁”在自动驾驶感知层,路面障碍物识别堪称“生命线工程”。传统视觉算法在复杂场景下常面临三重困境:雨天水雾导致特征模糊时漏检率高达25%,逆光环境下小目标(如碎石、井盖)检出率不足60%,而追求高精度又会导致帧率跌破20FPS,难以满足实时性要求[1]。某车企实测数据显示,传统YOLOv8在城郊混合路况中,因障碍物识别延迟引发的决策偏差占测试事故的37%,这些问题成为
- 打造智能资讯引擎:基于 Python 的新闻数据爬取与个性化推荐系统实战全流程解析
程序员威哥
最新爬虫实战项目python开发语言
前言:数据时代的信息洪流,如何做到“千人千面”?在信息爆炸的时代,每天都有成千上万条新闻资讯涌现。如何从海量内容中挖掘出用户感兴趣的资讯?这不仅仅是爬虫技术的问题,更是数据建模与智能推荐算法的落地挑战。本篇文章将带你从零出发,构建一个具有实际应用价值的“个性化新闻阅读推荐系统”,从数据采集(爬虫)、文本处理(NLP)、兴趣建模(TF-IDF/协同过滤/Embedding)到推荐展示,覆盖整个推荐系
- 题解 | #使用join查询找出没有分类的电影id以及名称#
愤怒的小青春
java
58同城java后端一面凉经主流的哈希算法有哪几种?帮闺蜜们找靠谱男票hc多多光彩积云是什么企业,查不到有用信息太抽象了!培训班装公司招聘阿里巴巴前端暑期实习——无语八面挂怎么写自我介绍|自我介绍保姆级教学灵犀互娱客户端一面面经(求过啊)24找运维实习,这简历可行吗拓竹科技测试开发面经(25届暑期实习)分享一波攒了整个秋招的NLP算法岗面经腾讯广告暑期实习面试1、JVM垃圾回收机制2、syncho
- 【算法题解】部分洛谷题解(下)
日月星辰cmc
算法分析与设计算法
前言本篇为我做过的洛谷题的部分题解,大多是我认为比较具有代表性的或者比较有意思的题目,包含我自己的思考过程和想法。[NOIP2001提高组]一元三次方程求解题目描述有形如:ax3+bx2+cx+d=0ax^3+bx^2+cx+d=0ax3+bx2+cx+d=0这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,da,b,c,da,b,c,d均为实数),并约定该方程存在三个不同实根(根的范围
- LeetCode - 3274. Check if Two Chessboard Squares Have the Same Color
阿蒙Armon
LeetCodeleetcode算法职场和发展
LeetCode-3274.CheckifTwoChessboardSquaresHavetheSameColor在LeetCode的算法题库中,有许多有趣的题目将实际场景与编程逻辑相结合,LeetCode3274题CheckifTwoChessboardSquaresHavetheSameColor便是其中之一。这道题以国际象棋棋盘为背景,要求我们判断给定的两个方格颜色是否相同。通过解决这道题,
- 算法竞赛备考冲刺必刷题(C++) | 洛谷 P1024 一元三次方程求解
热爱编程的通信人
c++算法开发语言
本文分享的必刷题目是从蓝桥云课、洛谷、AcWing等知名刷题平台精心挑选而来,并结合各平台提供的算法标签和难度等级进行了系统分类。题目涵盖了从基础到进阶的多种算法和数据结构,旨在为不同阶段的编程学习者提供一条清晰、平稳的学习提升路径。欢迎大家订阅我的专栏:算法题解:C++与Python实现!附上汇总贴:
- 监控漏检频发?陌讯YOLOv7实时优化方案召回率提升25%
2501_92489016
目标跟踪人工智能计算机视觉算法目标检测视觉检测智慧城市
一、开篇痛点在安防监控领域,传统目标检测模型面临三重困境:实时性差:1080P视频流处理普遍低于20FPS(VGG16仅15FPS)漏检率高:密集场景下小目标召回率常低于60%(COCO-val实测数据)部署成本高:ResNet-101需8GB显存,难以边缘化部署某智慧园区项目显示:夜间误报率高达34%,运维成本激增300%二、技术解析:陌讯SlimYOLO架构创新针对上述痛点,陌讯视觉算法提出三
- TensorFlow GPU 2.10.1 for Python 3.9快速安装指南
疑样
本文还有配套的精品资源,点击获取简介:TensorFlowGPU2.10.1是专为Windowsx64和Python3.9设计的TensorFlow版本,它集成了GPU支持以加快深度学习模型的训练。本指南提供了该版本的概述、安装步骤及注意事项,旨在帮助开发者利用其性能优势提升机器学习项目的效率。1.TensorFlowGPU介绍1.1TensorFlow的起源与功能TensorFlow是由Goog
- 进阶向:基于Python的智能客服系统设计与实现
智能客服系统开发指南系统概述智能客服系统是人工智能领域的重要应用,它通过自然语言处理(NLP)和机器学习技术自动化处理用户查询,显著提升客户服务效率和响应速度。基于Python的实现方案因其丰富的生态系统(如NLTK、spaCy、Transformers等库)、跨平台兼容性以及易于集成的特点,成为开发智能客服系统的首选。系统架构系统核心包括两个主要功能模块:1.API集成模块负责连接各类外部服务,
- JAVA刷题记录: 专题十五 BFS解决FloodFill算法
用屁屁笑
宽度优先算法
733.图像渲染-力扣(LeetCode)classSolution{int[]dx={0,0,-1,1};int[]dy={1,-1,0,0};publicint[][]floodFill(int[][]image,intsr,intsc,intcolor){intprev=image[sr][sc];if(color==prev)returnimage;Queueq=newLinkedList
- 14.优化算法之BFS解决FloodFill算法1
muyierfly
算法题算法宽度优先深度优先
0.FloodFill简介dfs:深度优先遍历(红色)bfs:宽度优先遍历1.图像渲染算法原理classSolution{int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};publicint[][]floodFill(int[][]image,intsr,intsc,intcolor){intprev=image[sr][sc];//统计刚开始的颜⾊if(prev==co
- BFS 解决 FloodFill 算法(C++)
lim 鹏哥
刷题算法宽度优先c++
文章目录前言一、概念二、岛屿数量1.题目链接2.算法原理3.代码编写三、被围绕的区域1.题目链接2.算法原理3.代码编写总结前言一、概念BFS就是广度优先遍历,也就是层序遍历。FloodFill是指在数组中找出性质相同的连通块,并根据题目进行操作。二、岛屿数量1.题目链接200.岛屿数量2.算法原理遍历整个矩阵,每找到一块陆地,记录一次。我们怎末知道我们是否已经遍历过这个地方了呢??方法1:如果遍
- BFS-FloodFill 算法 解决最短路问题 多源 解决拓扑排序
penguin_bark
#BFS算法宽度优先leetcode
文章目录一、FloodFill算法[733.图像渲染](https://leetcode.cn/problems/flood-fill/description/)2.思路3.代码[200.岛屿数量](https://leetcode.cn/problems/number-of-islands/description/)2.思路3.代码[LCR105.岛屿的最大面积](https://leetcod
- 机器学习专栏(62):手把手实现工业级ResNet-34及调优全攻略
目录一、ResNet革命性突破解析1.1残差学习核心思想1.2ResNet-34结构详解二、工业级Keras实现详解2.1数据预处理流水线2.2完整模型实现三、模型训练调优策略3.1学习率动态调整3.2混合精度训练四、性能优化技巧4.1分布式训练配置4.2TensorRT推理加速五、实战应用案例5.1医疗影像分类5.2工业质检系统六、模型可视化分析6.1特征热力图6.2参数量分析七、常见问题解决方
- 头盔识别误报率高?陌讯YOLOv7优化方案实测准确率达99%!
开篇痛点:算法失效的致命时刻在智慧交通领域,电动车头盔识别长期面临三大痛点:漏检危机:行人遮挡、雨天反光导致传统算法漏检率高达15%(某头部车企实测数据)误报泛滥:相似物体(背包、安全帽)误识别率超20%实时性缺陷:开源模型在1080P视频流中处理延时>200ms,无法满足实时预警需求技术解析:陌讯算法三重创新架构graphTDA[双路输入]-->B[多尺度特征融合模块]B-->C[空间注意力机制
- Dom
周华华
JavaScripthtml
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- 【Spark九十六】RDD API之combineByKey
bit1129
spark
1. combineByKey函数的运行机制
RDD提供了很多针对元素类型为(K,V)的API,这些API封装在PairRDDFunctions类中,通过Scala隐式转换使用。这些API实现上是借助于combineByKey实现的。combineByKey函数本身也是RDD开放给Spark开发人员使用的API之一
首先看一下combineByKey的方法说明:
- msyql设置密码报错:ERROR 1372 (HY000): 解决方法详解
daizj
mysql设置密码
MySql给用户设置权限同时指定访问密码时,会提示如下错误:
ERROR 1372 (HY000): Password hash should be a 41-digit hexadecimal number;
问题原因:你输入的密码是明文。不允许这么输入。
解决办法:用select password('你想输入的密码');查询出你的密码对应的字符串,
然后
- 路漫漫其修远兮 吾将上下而求索
周凡杨
学习 思索
王国维在他的《人间词话》中曾经概括了为学的三种境界古今之成大事业、大学问者,罔不经过三种之境界。“昨夜西风凋碧树。独上高楼,望尽天涯路。”此第一境界也。“衣带渐宽终不悔,为伊消得人憔悴。”此第二境界也。“众里寻他千百度,蓦然回首,那人却在灯火阑珊处。”此第三境界也。学习技术,这也是你必须经历的三种境界。第一层境界是说,学习的路是漫漫的,你必须做好充分的思想准备,如果半途而废还不如不要开始。这里,注
- Hadoop(二)对话单的操作
朱辉辉33
hadoop
Debug:
1、
A = LOAD '/user/hue/task.txt' USING PigStorage(' ')
AS (col1,col2,col3);
DUMP A;
//输出结果前几行示例:
(>ggsnPDPRecord(21),,)
(-->recordType(0),,)
(-->networkInitiation(1),,)
- web报表工具FineReport常用函数的用法总结(日期和时间函数)
老A不折腾
finereport报表工具web开发
web报表工具FineReport常用函数的用法总结(日期和时间函数)
说明:凡函数中以日期作为参数因子的,其中日期的形式都必须是yy/mm/dd。而且必须用英文环境下双引号(" ")引用。
DATE
DATE(year,month,day):返回一个表示某一特定日期的系列数。
Year:代表年,可为一到四位数。
Month:代表月份。
- c++ 宏定义中的##操作符
墙头上一根草
C++
#与##在宏定义中的--宏展开 #include <stdio.h> #define f(a,b) a##b #define g(a) #a #define h(a) g(a) int main() { &nbs
- 分析Spring源代码之,DI的实现
aijuans
springDI现源代码
(转)
分析Spring源代码之,DI的实现
2012/1/3 by tony
接着上次的讲,以下这个sample
[java]
view plain
copy
print
- for循环的进化
alxw4616
JavaScript
// for循环的进化
// 菜鸟
for (var i = 0; i < Things.length ; i++) {
// Things[i]
}
// 老鸟
for (var i = 0, len = Things.length; i < len; i++) {
// Things[i]
}
// 大师
for (var i = Things.le
- 网络编程Socket和ServerSocket简单的使用
百合不是茶
网络编程基础IP地址端口
网络编程;TCP/IP协议
网络:实现计算机之间的信息共享,数据资源的交换
协议:数据交换需要遵守的一种协议,按照约定的数据格式等写出去
端口:用于计算机之间的通信
每运行一个程序,系统会分配一个编号给该程序,作为和外界交换数据的唯一标识
0~65535
查看被使用的
- JDK1.5 生产消费者
bijian1013
javathread生产消费者java多线程
ArrayBlockingQueue:
一个由数组支持的有界阻塞队列。此队列按 FIFO(先进先出)原则对元素进行排序。队列的头部 是在队列中存在时间最长的元素。队列的尾部 是在队列中存在时间最短的元素。新元素插入到队列的尾部,队列检索操作则是从队列头部开始获得元素。
ArrayBlockingQueue的常用方法:
- JAVA版身份证获取性别、出生日期及年龄
bijian1013
java性别出生日期年龄
工作中需要根据身份证获取性别、出生日期及年龄,且要还要支持15位长度的身份证号码,网上搜索了一下,经过测试好像多少存在点问题,干脆自已写一个。
CertificateNo.java
package com.bijian.study;
import java.util.Calendar;
import
- 【Java范型六】范型与枚举
bit1129
java
首先,枚举类型的定义不能带有类型参数,所以,不能把枚举类型定义为范型枚举类,例如下面的枚举类定义是有编译错的
public enum EnumGenerics<T> { //编译错,提示枚举不能带有范型参数
OK, ERROR;
public <T> T get(T type) {
return null;
- 【Nginx五】Nginx常用日志格式含义
bit1129
nginx
1. log_format
1.1 log_format指令用于指定日志的格式,格式:
log_format name(格式名称) type(格式样式)
1.2 如下是一个常用的Nginx日志格式:
log_format main '[$time_local]|$request_time|$status|$body_bytes
- Lua 语言 15 分钟快速入门
ronin47
lua 基础
-
-
单行注释
-
-
[[
[多行注释]
-
-
]]
-
-
-
-
-
-
-
-
-
-
-
1.
变量 & 控制流
-
-
-
-
-
-
-
-
-
-
num
=
23
-
-
数字都是双精度
str
=
'aspythonstring'
- java-35.求一个矩阵中最大的二维矩阵 ( 元素和最大 )
bylijinnan
java
the idea is from:
http://blog.csdn.net/zhanxinhang/article/details/6731134
public class MaxSubMatrix {
/**see http://blog.csdn.net/zhanxinhang/article/details/6731134
* Q35
求一个矩阵中最大的二维
- mongoDB文档型数据库特点
开窍的石头
mongoDB文档型数据库特点
MongoDD: 文档型数据库存储的是Bson文档-->json的二进制
特点:内部是执行引擎是js解释器,把文档转成Bson结构,在查询时转换成js对象。
mongoDB传统型数据库对比
传统类型数据库:结构化数据,定好了表结构后每一个内容符合表结构的。也就是说每一行每一列的数据都是一样的
文档型数据库:不用定好数据结构,
- [毕业季节]欢迎广大毕业生加入JAVA程序员的行列
comsci
java
一年一度的毕业季来临了。。。。。。。。
正在投简历的学弟学妹们。。。如果觉得学校推荐的单位和公司不适合自己的兴趣和专业,可以考虑来我们软件行业,做一名职业程序员。。。
软件行业的开发工具中,对初学者最友好的就是JAVA语言了,网络上不仅仅有大量的
- PHP操作Excel – PHPExcel 基本用法详解
cuiyadll
PHPExcel
导出excel属性设置//Include classrequire_once('Classes/PHPExcel.php');require_once('Classes/PHPExcel/Writer/Excel2007.php');$objPHPExcel = new PHPExcel();//Set properties 设置文件属性$objPHPExcel->getProperties
- IBM Webshpere MQ Client User Issue (MCAUSER)
darrenzhu
IBMjmsuserMQMCAUSER
IBM MQ JMS Client去连接远端MQ Server的时候,需要提供User和Password吗?
答案是根据情况而定,取决于所定义的Channel里面的属性Message channel agent user identifier (MCAUSER)的设置。
http://stackoverflow.com/questions/20209429/how-mca-user-i
- 网线的接法
dcj3sjt126com
一、PC连HUB (直连线)A端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 二、PC连PC (交叉线)A端:(568A): 白绿,绿,白橙,蓝,白蓝,橙,白棕,棕; B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 三、HUB连HUB&nb
- Vimium插件让键盘党像操作Vim一样操作Chrome
dcj3sjt126com
chromevim
什么是键盘党?
键盘党是指尽可能将所有电脑操作用键盘来完成,而不去动鼠标的人。鼠标应该说是新手们的最爱,很直观,指哪点哪,很听话!不过常常使用电脑的人,如果一直使用鼠标的话,手会发酸,因为操作鼠标的时候,手臂不是在一个自然的状态,臂肌会处于绷紧状态。而使用键盘则双手是放松状态,只有手指在动。而且尽量少的从鼠标移动到键盘来回操作,也省不少事。
在chrome里安装 vimium 插件
- MongoDB查询(2)——数组查询[六]
eksliang
mongodbMongoDB查询数组
MongoDB查询数组
转载请出自出处:http://eksliang.iteye.com/blog/2177292 一、概述
MongoDB查询数组与查询标量值是一样的,例如,有一个水果列表,如下所示:
> db.food.find()
{ "_id" : "001", "fruits" : [ "苹
- cordova读写文件(1)
gundumw100
JavaScriptCordova
使用cordova可以很方便的在手机sdcard中读写文件。
首先需要安装cordova插件:file
命令为:
cordova plugin add org.apache.cordova.file
然后就可以读写文件了,这里我先是写入一个文件,具体的JS代码为:
var datas=null;//datas need write
var directory=&
- HTML5 FormData 进行文件jquery ajax 上传 到又拍云
ileson
jqueryAjaxhtml5FormData
html5 新东西:FormData 可以提交二进制数据。
页面test.html
<!DOCTYPE>
<html>
<head>
<title> formdata file jquery ajax upload</title>
</head>
<body>
<
- swift appearanceWhenContainedIn:(version1.2 xcode6.4)
啸笑天
version
swift1.2中没有oc中对应的方法:
+ (instancetype)appearanceWhenContainedIn:(Class <UIAppearanceContainer>)ContainerClass, ... NS_REQUIRES_NIL_TERMINATION;
解决方法:
在swift项目中新建oc类如下:
#import &
- java实现SMTP邮件服务器
macroli
java编程
电子邮件传递可以由多种协议来实现。目前,在Internet 网上最流行的三种电子邮件协议是SMTP、POP3 和 IMAP,下面分别简单介绍。
◆ SMTP 协议
简单邮件传输协议(Simple Mail Transfer Protocol,SMTP)是一个运行在TCP/IP之上的协议,用它发送和接收电子邮件。SMTP 服务器在默认端口25上监听。SMTP客户使用一组简单的、基于文本的
- mongodb group by having where 查询sql
qiaolevip
每天进步一点点学习永无止境mongo纵观千象
SELECT cust_id,
SUM(price) as total
FROM orders
WHERE status = 'A'
GROUP BY cust_id
HAVING total > 250
db.orders.aggregate( [
{ $match: { status: 'A' } },
{
$group: {
- Struts2 Pojo(六)
Luob.
POJOstrust2
注意:附件中有完整案例
1.采用POJO对象的方法进行赋值和传值
2.web配置
<?xml version="1.0" encoding="UTF-8"?>
<web-app version="2.5"
xmlns="http://java.sun.com/xml/ns/javaee&q
- struts2步骤
wuai
struts
1、添加jar包
2、在web.xml中配置过滤器
<filter>
<filter-name>struts2</filter-name>
<filter-class>org.apache.st