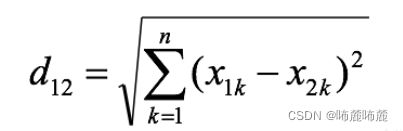K-means算法（知识点梳理）

目录

一.K-means算法的原理和工作流程

1.算法原理

2.工作流程

二.K-means中常用的距离度量方法

1.欧几里得距离（欧氏距离）

2.曼哈顿距离

3.切比雪夫距离

三.K-means算法中K值的选择

1.手肘法

2. 轮廓系数

        手肘法和轮廓系数的实现

四.初始点的选择

1.随机选择

2.最远距离       

3.层次聚类或canopy预处理

五.陷入质心的循环停不下来怎么办

1.原因

2.怎么办 

六.K-means算法与KNN算法的共同点与区别

1.区别

2.共同点

七.K-means算法的优缺点

1.K-means算法的优点

2.K-means算法的缺点

八.根据K-means算法的缺点，有哪些改进的算法

1.K-means++

2.ISODATA

3.Kernel K-means

九.如何对K-means进行算法调优

十.K-means算法实现

---

一.K-means算法的原理和工作流程

1.算法原理

        K-means算法是基于原型的，根据距离划分组的无监督聚类算法，对于给定的样本集，按照样本间的距离大小，将样本划分为K个簇，使得簇内的点尽量紧密相连，而簇间的点距离尽量大。

2.工作流程

        step1：随机选取K个点作为聚类中心，即k个类中心向量

        step2：分别计算其他样本点到各个类中心向量的距离，并将其划分到距离最近的类

        step3：更新各个类的中心向量

        step4：判断新的类中心向量是否发生改变，若发生改变则转到step2，若类中心向量不再发生变化，停止并输出聚类结果

二.K-means中常用的距离度量方法

1.欧几里得距离（欧氏距离）

        

        衡量多维空间中的两点间距离，也是最常用的距离度量方法。

2.曼哈顿距离

      

         曼哈顿距离也叫出租车距离，用来标明两个点在标准坐标系上的绝对轴距总和。

3.切比雪夫距离

        

三.K-means算法中K值的选择

        思考：如果我们的数据是关于色彩RGB数据，我们可以直接设置K为3对图片的参数进行聚类分析，这是在我们已知数据基本信息的前提下采取的策略。但是，如果我们并不知道数据的基本信息，怎么分类，分成几类就是我们不得不思考的问题，这时，我们更希望能够从数据的角度出发，判断这一组数据希望自己分成几类，即K为几时分类效果最好。

1.手肘法

        1.简单描述手肘法

        手肘法是最常用的确定K-means算法K值的方法，所用到的衡量标准是SSE（sum of the squared errors，误差平方和）  

        主要思想：当k小于真实聚类数时，随着k的增大，会大幅提高类间聚合程度，SSE会大幅下降，当k达到真实聚类数时，随着k的增加，类间的聚合程度不会大幅提高，SSE的下降幅度也不会很大，所以k/SSE的折线图看起来像一个手肘，我们选取肘部的k值进行运算。

                

2. 轮廓系数

        1.简单描述轮廓系数

                使用轮廓系数时，先假设已经将样本集分成了k个簇，针对每个点，计算其轮廓系数

                轮廓系数公式：

                        

                其中a(i)是样本点x(i)对同簇其他样本点的平均距离，称为凝聚度；b(i)是样本点x(i)到最近簇所有样本的平均距离，称为分离度。

                最近簇定义如下：

                        

                 就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。

                求出所有点的轮廓系数再求平均值就得出了平均轮廓系数，平均轮廓系数的取值在[-1,1],显然，由轮廓系数公式可以观察出，凝聚度越小，分离度越大，分类效果越好，平均轮廓系数也越大，所以，取平均轮廓系数最大的点的k值时，分类效果越好

        手肘法和轮廓系数的实现

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans

data=pd.read_excel(r'C:\Users\21091\Downloads\wine.xlsx')

scores=[]  #存放轮廓系数
distortions=[]#簇内误差平方和  SSE
for i in range(2,10):
    Kmeans_model=KMeans(n_clusters=i)
    predict_=Kmeans_model.fit_predict(data)
    scores.append( silhouette_score(data,predict_))
    distortions.append(Kmeans_model.inertia_)
print("轮廓系数：",scores)
print("簇内误差平方和：",distortions)

#SSE  手肘法
plt.plot(range(2,10),distortions,marker='x')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.title('distortions')
plt.show()

#轮廓系数法
plt.plot(range(2,10),scores,marker='x')
plt.xlabel('Number of clusters')
plt.ylabel('scores')
plt.title('scores')
plt.show()

运行结果

                        

四.初始点的选择

1.随机选择

           顾名思义，随机选取k个点作为初始点

2.最远距离       

        先选取1个点作为聚类中心，遍历其余所有样本点，选择距离最远的样本点作为第二个聚类中心，计算这两个点的中心向量，再次遍历样本点，找到最远的点作为第三个聚类中心，迭代直至找到k个点。

3.层次聚类或canopy预处理

        先得到k个簇，再从每个簇中选择一个点，该点可以是中心点，也可以是离中心点最近的点。

五.陷入质心的循环停不下来怎么办

1.原因

        可能样本数据本身不收敛

2.怎么办 

        1.进行迭代次数设置

        2.设定收敛判断距离

六.K-means算法与KNN算法的共同点与区别

1.区别

        1.K-means算法是聚类算法，无监督学习；KNN算法是分类算法，监督学习

        2.K-means算法与KNN算法中的K值含义不同

                K-means算法是将样本聚类成K个类；KNN算法是将输入数据的特征与样本集中数据的特征进行比较，取最相似的K个数据，若其中X类数据占大部分，则将这个输入数据划分为X类。

        3.K-means算法有明显的前期训练过程，KNN算法没有。

2.共同点

        都用到了NN（Nears Neighbor）算法 ，即根据一个点，在样本集中找到离它最近的点。

七.K-means算法的优缺点

1.K-means算法的优点

       （1）原理简单，容易实现
       （2）可解释度较强

2.K-means算法的缺点

        （1）K值很难确定
        （2）局部最优
        （3）对噪音和异常点敏感
        （4）需样本存在均值（限定数据种类）
        （5）聚类效果依赖于聚类中心的初始化
        （6）对于非凸数据集或类别规模差异太大的数据效果不好

八.根据K-means算法的缺点，有哪些改进的算法

1.K-means++

              利用距离越远越好的策略选取初始点

2.ISODATA

                当属于某个类的样本点过少时，把这个类去掉；当属于某个类的样本点过多且分散时，将这个类分为两个类

3.Kernel K-means

                参照支持向量机中核函数的定义，将所有样本映射到另外一个特征空间中再进行聚类，有可能改善聚类效果。

九.如何对K-means进行算法调优

1.数据归一化和离散点处理

2.合理选择k值

3.使用核方法

十.K-means算法实现

          烦请移步我的另一篇博客：

        https://blog.csdn.net/weixin_46336091/article/details/123881505