机器学习从零到入门 GBDT 梯度提升决策树
GBDT 梯度提升决策树详解
- 一、 梯度的概念
-
- 1、日常生活中的梯度
- 2、函数中的梯度
-
- 2.1、走进数学
- 2.2、从数学到机器学习
-
- (1)、损失函数的理解 loss function
- (2)、梯度的理解 gradient
- (3)、损失函数的梯度下降
- 二、GBDT
-
- 1、回归树 - Regression Decision Tree,DT
- 2、梯度提升 - Gradient Boosting - GB
- 3、提升树 - Boosting Desicion Tree - BDT
- 三、GBDT的应用
-
- 1、GBDT 函数参数与方法
- 2、案例:推荐系统预测模型 GBDT+LR
-
- 2.1、背景介绍
- 2.2、深入了解
- 2.3、算法Demo演示
- 参考
- 更新时间
一、 梯度的概念
在开始了解GBDT之前,需要先需要了解,什么是梯度?
1、日常生活中的梯度
梯度使用陡峭程度来衡量,拿日常生活中骑自行车为例,如下图所示(从左到右,从上到下):
- 图一向上比较陡峭,有很高的的
正梯度(positive gradient) - (k >0) - 图二相对平缓,有很低的梯度(lower gradient) (k!=0)
- 图三是平坦的,梯度为0 - (k=0)
- 图四向下比较陡峭,有很高的的
负梯度(negative gradient) - (k<0)

2、函数中的梯度
2.1、走进数学
那么在数学应用中如何寻找梯度(gradient)?
学生时代我们都知道,梯度实际上表示的是斜率 k k k,意思是函数的变化率,也就是函数所描绘的线的方向往哪偏往哪走(向 x x x或 y y y偏),比如:
直线 y = 2 x + 3 y=2x+3 y=2x+3,这条线,通过求导可得 k = ∂ y ∂ x = 2 \begin{aligned} k=\frac{\partial y}{\partial x} \end{aligned}=2 k=∂x∂y=2
因为 k k k 是常数, x x x与 y y y成正比,线性关系。

直线 y = x 2 + 3 y=x^2+3 y=x2+3,这条线,通过求导可得 k = ∂ y ∂ x = 2 x \begin{aligned} k=\frac{\partial y}{\partial x} \end{aligned}=2x k=∂x∂y=2x
因为 k k k 不是常数,带有 x x x,偏向于在单位 y y y 值内,让 x x x 值比平常多一个幂值, y y y 与 x x x 的直线会被拉伸为曲线。

上面的函数中,我们输入一个 x x x 值,就能求得 y y y 值,就像根据 x x x 去预测 y y y 一样,这就像已经获得了一个分类器或者回归器,输入样本得出结果。
然而上面的函数是怎么求得的?其实还是通过最原始的点去计算得到的,我们通过点计算 k k k 就大致清楚了这个函数到底是哪一种,线性函数?那我们用 y = k x + b y=kx+b y=kx+b 去表达(针对二元一次函数,当然其他种类很多),带入点进行计算;幂函数?那我们用 y = c 0 + c 1 x k y=c_0+c_1x^k y=c0+c1xk。
这是我们通过 k k k 和 点 ( x , y ) (x,\ y) (x, y) 再是已知的函数框架来求得函数的(拟合机器),然而,对于海量的数据点,复杂度过高的函数,可能没有可套用的函数框架,我们得站在高维的方式去解决问题,比如机器学习。
机器学习内部也是一套复杂的数学函数+算法逻辑,所以我们大致也可以将每个机器学习模型看成前面的函数框架,然而这个框架可能过于复杂,我们不可能像前面那样,直接根据数据集就能推断,是属于哪个函数框架(机器学习模型),所以在机器学习中,我们也会尝试用多个不同模型去拟合数据得出效果最好的模型。
2.2、从数学到机器学习
(1)、损失函数的理解 loss function
在机器学习中,我们并不知道这样的函数长什么样,数学公式怎么表达,图像上怎么画的,我们只知道我们有很多数据集,即我们只有坐标点,那么我们就要用点去近似模拟出这个函数。
可能第一次不对,但是我们可以不断地更改尝试,直到得到一个近似的关于 x x x 函数,把现有的点的 x x x带入该函数,可能不能得到正确的 y y y (即求得的 y ′ y^{'} y′与真实值 y y y不同)。
但是,在不断的修正过程中,如果某个函数能使得到的误差值(或叫做损失loss) ∣ y ′ − y ∣ |y^{'}-y| ∣y′−y∣的值的总和最小(这就是机器学习中的损失函数的一种表达方式,绝对误差,表示为 ∑ i = 1 n ∣ y i ′ − y ∣ \sum^n_{i=1}|y_i^{'}-y| ∑i=1n∣yi′−y∣),那么这就是一个非常完美的机器(函数)了。
所以,我们从上述可以明白,损失函数是一种用来衡量函数结果好坏的标准,损失越小,我们构造的函数就越接近那个隐藏的真实函数的标准答案。
但是在机器学习中,对损失函数又进行了优化,所以在不同的场景中,有不同的损失函数:
- 铰链损失(Hinge Loss):主要用于支持向量机(SVM) 中;
- 互熵损失 (Cross Entropy Loss,Softmax Loss ):用于Logistic 回归与Softmax 分类中;
- 平方损失(Square Loss):主要是最小二乘法(OLS)中;
- 指数损失(Exponential Loss) :主要用于Adaboost 集成学习算法中;
- 其他损失(如0-1损失,绝对值损失)
其中,平方损失是一种比较简单且常用的损失函数,对于N个样本,它的损失函数表示为: 1 2 ∑ i = 1 n ( y − f ( x ) ) 2 \begin{aligned}\frac{1}{2}\sum^n_{i=1}(y-f(x))^2\end{aligned} 21i=1∑n(y−f(x))2,加上 1 2 \frac{1}{2} 21是为了求导方便,为什么要求导呢?求导是为了寻找极小值,寻找梯度接近0时的 f ( x ) f(x) f(x),此时 f ( x ) f(x) f(x)与 y y y的值最接近。
y − f ( X ) y−f(X) y−f(X) 表示残差或叫损失,整个式子表示的是残差平方和 ,通过上面的概念我们知道,我们的目标就是最小化这个目标函数值,即最小化残差的平方和。
(2)、梯度的理解 gradient
理解了损失函数,我们再来看看另一个概念:梯度。
梯度是微积分中一个很重要的概念,它是函数变化最快的方向,一旦它为零,即表示不会再变化,也就达到了极值点:
- 在单变量的函数中,梯度其实就是函数的微分,因为斜率方向 y y y增长最快,所以这个梯度代表着函数在某个给定点的切线的斜率,这个比较简单,如下图的例子所示:
先从下列一条简单的直线为例,如果我们先只知道两个点, ( x 1 , y 1 ) (x_1,\ y_1) (x1, y1)和 ( x 2 , y 2 ) (x_2,\ y_2) (x2, y2),通过学生时代的知识,我们知道:梯度 ∇ w = k = y 1 − y 2 x 1 − x 2 = Δ y Δ x \nabla{w}=\begin{aligned} k=\frac{y_1-y_2}{x_1-x_2}=\frac{\Delta{y}}{\Delta{x}} \end{aligned} ∇w=k=x1−x2y1−y2=ΔxΔy 对应下图中的直线,我们得到 k = 0.5 1 = 0.5 \begin{aligned} k=\frac{0.5}{1}=0.5 \end{aligned} k=10.5=0.5

对于该函数: y = f ( x ) = 0.5 x + 1 y=f(x)=0.5x+1 y=f(x)=0.5x+1
梯度为直接求导: 0.5 0.5 0.5
- 在多变量函数中,梯度就是分别对每个变量进行微分,它是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升或下降最快的方向。
例如: y = f ( x , z ) = 3 x + 9 z y=f(x,z)=3x+9z y=f(x,z)=3x+9z
分别对 x , z x,z x,z求导,梯度为: < 3 , 9 > <3,9> <3,9>
微分,梯度及梯度下降法(csdn)
(3)、损失函数的梯度下降
为什么要求损失函数的梯度下降?因为我们要找到损失函数的最小值,即梯度下降接近0的地方,就是我们要找的最合适的函数。
函数的设定:
我们假设损失函数为平方损失函数,形式如下:
L o s s = 1 2 ∑ i = 1 n ( y − f ( x ) ) 2 Loss=\begin{aligned}\frac{1}{2}\sum^n_{i=1}(y-f(x))^2\end{aligned} Loss=21i=1∑n(y−f(x))2
y − f ( x ) y-f(x) y−f(x)是真实值和预测值的差,我们打包写成 w w w,变成一个一元二次方程。
L o s s = f ( w ) = 1 2 ∑ i = 1 n w 2 Loss=f(w)=\begin{aligned}\frac{1}{2}\sum^n_{i=1}w^2\end{aligned} Loss=f(w)=21i=1∑nw2
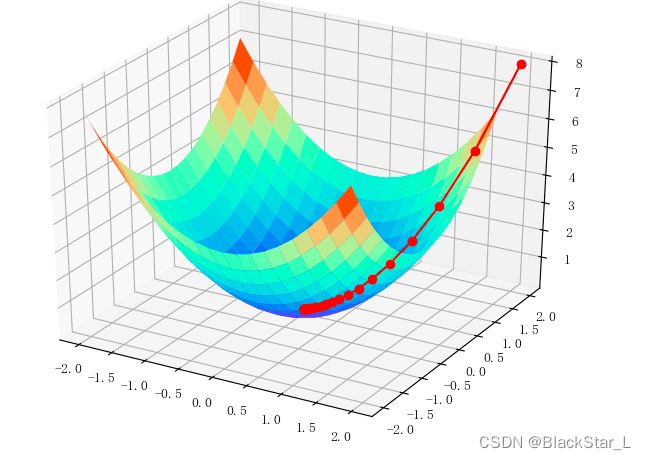
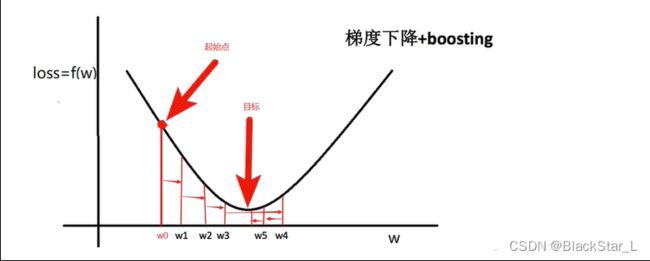
我们将 x x x 轴设为 w w w, y y y 轴设为损失函数的值,我们要找 w i w_i wi梯度的下降梯度,且该下降梯度接近0 (如果该下降梯度为0,与函数最底部相切,那么此时损失值Loss最小,那么这个点的梯度拟合的曲线最佳,于是我们假设该函数曲线如下:

我们开始进行梯度下降:
-
先随机选择一个点 w 0 w_0 w0。然后,因为我们知道了损失函数,对其进行求导,找到它的梯度函数: d f ( w i ) d w i = w i \begin{aligned}\frac{d_{f(w_i)}}{d_{w_i}}=w_i\end{aligned} dwidf(wi)=wi,带入 w 0 w_0 w0,梯度值为 ∇ f ( w 0 ) = w 0 \begin{aligned}\nabla{f(w_0)}\end{aligned}=w_0 ∇f(w0)=w0。
-
设定 α \alpha α - learning rate,梯度下降的程度。该值要与上一步的梯度值相乘,变成下一步移动的步长, α \alpha α的设置不可过大或者过小,过大可能错过极小值,过小可能到达极小值的时间过长。但最终会变成为小数或者动态逐渐减小,也就是移动的步长会变小,防止在最低点两侧徘徊。

-
进行迭代,直到 w i w_i wi接近0。迭代公式为:下一个点 w 1 = w 0 − α × ∇ f ( w 0 ) w_1=w_0-\alpha\times\nabla{f(w_0)} w1=w0−α×∇f(w0)。
从 w 0 w_0 w0 到 w 5 w_5 w5 具体的步骤如下:
w 1 = w 0 − α ∇ f ( w 0 ) w_1=w_0-\alpha\nabla f(w_0) w1=w0−α∇f(w0)
w 2 = w 1 − α ∇ f ( w 1 ) w_2=w_1-\alpha\nabla f(w_1) w2=w1−α∇f(w1)
w 3 = w 2 − α ∇ f ( w 2 ) w_3=w_2-\alpha\nabla f(w_2) w3=w2−α∇f(w2)
w 4 = w 3 − α ∇ f ( w 3 ) w_4=w_3-\alpha\nabla f(w_3) w4=w3−α∇f(w3)
w 5 = w 4 − α ∇ f ( w 4 ) w_5=w_4-\alpha\nabla f(w_4) w5=w4−α∇f(w4)
最后,通过6个点计算的值为:
w 5 = w 0 − α ∇ f ( w 0 ) − α ∇ f ( w 1 ) − α ∇ f ( w 2 ) − α ∇ f ( w 3 ) − α ∇ f ( w 4 ) w_5=w_0-\alpha\nabla f(w_0)-\alpha\nabla f(w_1)-\alpha\nabla f(w_2)-\alpha\nabla f(w_3)-\alpha\nabla f(w_4) w5=w0−α∇f(w0)−α∇f(w1)−α∇f(w2)−α∇f(w3)−α∇f(w4)
如果 w 5 w_5 w5最小,则此时的 L o s s Loss Loss最小,拟合的 f ( x ) f(x) f(x)函数最接近 y y y,机器就会选用最终的 f ( x ) f(x) f(x)去测试其他的 x x x得出更正确的 y y y值。
如果 w 5 w_5 w5并不是最小,可能经过了最低点或者根本没有达到最低点,说明学习率 α \alpha α可能设置的有问题,结果可能过拟合或者欠拟合。
二、GBDT
梯度提升决策树(Gradient Boosting Decision Tree, GBDT),是一种迭代的决策树算法(Multiple Additive Regression Tree, MART),该算法由多棵决策树组成,所有树的结论累加起来作为最终结果。
GBDT是泛化能力较强的算法,用到的决策树是回归树,用来做回归预测,调整后也可用于分类问题。
GBDT主要由三个概念组成:回归树(Decision Tree)、梯度提升(Gradient)、提升树(Boosting)。
1、回归树 - Regression Decision Tree,DT
决策树分为两大类:回归树和分类树。前者用于预测实数值,如明天的温度、用户的年龄、网页的相关程度;后者用于分类标签值,如晴天/阴天/雾/雨、用户性别、网页是否是广告页面等。GBDT的核心在于累加所有树的结果作为最终的结果,而分类树的结果是没有办法累加的,因此GBDT中的树都是回归树,不是分类树。
回归树总体流程类似于分类树,区别在于,回归树的每一个节点都会得到一个预测值,以下表中年龄预测为例:
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 年龄(年) | |
|---|---|---|---|---|
| x 1 x_1 x1 | 5000 | 7.5 | 165 | 19 |
| x 2 x_2 x2 | 5000 | 8.5 | 170 | 21 |
| x 3 x_3 x3 | 8000 | 7.5 | 170 | 29 |
| x 4 x_4 x4 | 8000 | 8.5 | 165 | 31 |
x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4 这四个职工年龄分别是19、21、29 和 31,样本中有工资、睡觉时间、身高等特征,每一个节点的预测值等于属于这个节点的所有人年龄的平均值,如下图:
第一个根节点是所有样本的年龄,25是平均值,即预测值。
后面两个子节点是根据工资这个特征进行划分的,同样也用平均值作为预测值。

分支时,通过穷举每一个特征的每一个阈值,寻找最好的分割点,但衡量最好的标准不是最大熵,而是最小化平方差。也就是被预测错的越多或者越远,平方误差就越大,通过最小化平方误差能够找到最可靠的分支依据。分枝直到每个叶子节点上人的年龄都唯一或者达到预设的终止条件(如回归树个数的上限),如果最终叶子节点上人的年龄不唯一,则以该节点上所有人的平均年龄作为该叶子节点的预测年龄。
2、梯度提升 - Gradient Boosting - GB
梯度提升其实是一个算法框架,可以将已有的分类或回归算法放入其中,从而得到一个性能很强大的算法。梯度提升需要进行多次迭代,每次迭代产生一个模型,需要让每次产生的模型对训练集的损失函数最小。如何让损失函数越来越小呢?采用梯度下降的方法,在每次迭代时通过向损失函数的负梯度方向移动来使损失函数越来越小,这样可以得到越来越精确的模型。
常见的损失函数有 log \log log 损失、平方误差和绝对误差等。 log \log log损失常用于分类任务,平方误差和绝对误差常用于回归任务,损失函数与其对应的负梯度列表信息,如下所示:
| 损失函数 | 任务 | 表达式 | − ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) \begin{aligned}\frac{-\partial L(y_i,F_{(x_i)})} {\partial F(x_i)}\end{aligned} ∂F(xi)−∂L(yi,F(xi)) |
|---|---|---|---|
| log \log log损失函数 | 分类 | 2 log ( 1 + exp ( − 2 y i F ( x i ) ) ) 2\log(1+\exp(-2y_iF(x_i))) 2log(1+exp(−2yiF(xi))) | 4 y ( 1 + exp ( 2 y F ( x i ) ) ) \begin{aligned}\frac{4y}{(1+\exp(2yF(x_i)))}\end{aligned} (1+exp(2yF(xi)))4y |
| 平方误差 | 回归 | ( y i − F ( x i ) ) 2 (y_i-F(x_i))^2 (yi−F(xi))2 | 2 ( y i − F ( x i ) ) 2(y_i-F(x_i)) 2(yi−F(xi)) |
| 绝对误差 | 回归 | y_i-F(x_i) | s i g n ( y i − F ( x i ) ) sign(y_i-F(x_i)) sign(yi−F(xi)) |
学习算法的目标是为了优化或者说误差最小化,梯度提升的思想是迭代多个 ( M M M 个) 弱学模型,将每个弱学习模型的预测结果相加,后面的模型 F m + 1 ( x ) F_{m+1}(x) Fm+1(x) 是基于前面模型 F m ( x ) F_{m}(x) Fm(x) 生成的,关系如下:
F m + 1 = F m ( x ) + h ( x ) ( 1 ≤ m ≤ M ) \begin{aligned}F_{m+1}=F_m(x)+h(x)\end{aligned}\\ (1\le{m}\le{M}) Fm+1=Fm(x)+h(x)(1≤m≤M)
梯度提升的思想很简单,关键是如何生成 h ( x ) h(x) h(x)。如果损失函数是回归问题中的平方误差,那么 h ( x ) h(x) h(x) 是能够通过 2 ( y − F m ( x ) ) 2(y-F_m(x)) 2(y−Fm(x)) 函数进行拟合,这就是基于残差的学习。残差学习在回归问题中能被很好的使用,但是在一般情况下(分类,排序等问题),往往是基于损失函数在函数空间的负梯度学习。
梯度提升的具体步骤:
- 初始化模型为常数值 F 0 ( x ) = arg min γ ∑ i = 1 n L ( y i , γ ) F_0(x)=\argmin_\gamma\sum^n_{i=1}L(y_i,\gamma) F0(x)=argminγ∑i=1nL(yi,γ)
- 迭代生成 M M M 个基学习器
(1). 计算负梯度: r i m = − [ − ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) ( i = 1 , . . . . ) \begin{aligned}r_{im}=-[\frac{-\partial L(y_i,F_{(x_i)})} {\partial F(x_i)}]_{F(x)=F_{m-1}(x)}\end{aligned}\ (i=1,....) rim=−[∂F(xi)−∂L(yi,F(xi))]F(x)=Fm−1(x) (i=1,....)
(2). 基于 { ( x i , γ i m ) } i = 1 n \{(x_i,\gamma_{im})\}^n_{i=1} {(xi,γim)}i=1n 生成基学习器 h m ( x ) h_m(x) hm(x)
(3). 计算最优的 γ m \gamma_m γm, γ m = arg min r ∑ i = 1 n L ( y i , F m − 1 ( x i ) + γ h m ( x i ) ) \begin{aligned}\gamma_m=\argmin_r\sum^n_{i=1}L(y_i,F_{m-1}(x_i)+\gamma h_m(x_i))\end{aligned} γm=rargmini=1∑nL(yi,Fm−1(xi)+γhm(xi))
(4). 更新模型 F m ( x ) = F m − 1 ( x ) + γ h m ( x i ) F_m(x)=F_{m-1}(x)+\gamma h_m(x_i) Fm(x)=Fm−1(x)+γhm(xi)
想深入理解可以学习这个论文 Greedy function Approximation – A Gradient Boosting Machine,核心思想就是:算法在每一轮迭代中,先计算出当前模型在所有样本上的负梯度,然后以该值为目标训练一个新的弱分类器进行拟合并计算出该弱分类器的权重,最终实现对模型的更新。

3、提升树 - Boosting Desicion Tree - BDT
提升树是迭代多棵回归树进行共同决策,当采用平方误差损失函数时,每一棵回归树学习的是之前所有树的结论和残差,拟合得到一个当前的残差回归树,残差=真实值-预测值,但此处要拟合的是2倍的残差。提升树最终结果是整个迭代过程生成的回归树的累加。
使用上面1回归树章节中的表中的 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4四个职工的数据:
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 年龄(年) | |
|---|---|---|---|---|
| x 1 x_1 x1 | 5000 | 7.5 | 165 | 19 |
| x 2 x_2 x2 | 5000 | 8.5 | 170 | 21 |
| x 3 x_3 x3 | 8000 | 7.5 | 170 | 29 |
| x 4 x_4 x4 | 8000 | 8.5 | 165 | 31 |
损失函数使用 ( y i − F ( x i ) 2 (y_i-F(x_i)^2 (yi−F(xi)2,负梯度是 2 ( y i − F ( x i ) ) 2(y_i-F(x_i)) 2(yi−F(xi)),一棵提升树的学习过程,如下图所示:

如图所示,预测值等于两个回归树值的累加,如 x 1 x_1 x1 的预测值为树1左节点预测值(20) + 树2左节点预测值(-2)=18。
GBDT利用加法模型(即基函数的线性组合)与向前分布算法实现学习的优化过程,其中以二叉回归树作为基函数,损失函数采用平方误差函数,每一步的优化简单,当前模型只需要拟合残差。
将GBDT算法叙述如下:
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1),\ (x_2,y_2),\ ...,\ (x_n,y_n)\} T={(x1,y1), (x2,y2), ..., (xn,yn)}
输出: 提升树 f M ( x ) f_M(x) fM(x)
(1). 初始化一棵决策树 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0,估计一个损失函数 (这里损失函数可以设为 1 2 ( y − f m − 1 ( x ) ) 2 \begin{aligned}\frac{1}{2}(y-f_{m-1}(x))^2\end{aligned} 21(y−fm−1(x))2 前面可加上任意常数不影响,加上1/2便于求导消去2) ,计算该损失函数的负梯度公式,即为残差(Residual): r m i = ( y i − f m − 1 ( x i ) ) , i = 1 , 2 , . . . , n r_{mi}=(y_i-f_{m-1}(x_i)),\ i=1,2,...,n rmi=(yi−fm−1(xi)), i=1,2,...,n,其中 y i y_i yi为真实值, f m − 1 ( x i ) f_{m-1}(x_i) fm−1(xi)为累加的预测值(均值)。有时残差公式会写成: r m i = ( y i − α f m − 1 ( x i ) ) r_{mi}=(y_i-\alpha f_{m-1}(x_i)) rmi=(yi−αfm−1(xi)),其中 α \alpha α 表示学习率,含义为梯度下降的程度,目的是防止过拟合。
(2). 不断迭代提升,对 m = 1 , 2 , . . . , M m=1,2,...,M m=1,2,...,M 构建树模型
a). 求解划分点。枚举每一个阈值,寻找最好的切分点,可以使用平均平方误差来比较。
b). 计算残差,拟合残差 r m i r_{mi} rmi 学习得到一个回归树 T ( x ; θ m ) T(x;\theta_m) T(x;θm)
c). 更新 f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) f_m(x)=f_{m-1}(x)+T(x;\theta_m) fm(x)=fm−1(x)+T(x;θm),这棵回归树的结果等于上一棵回归树的结果+这棵回归树
d). 保留残差作为下一棵树的输入值,或者达到停止条件(树的数量)则停止。
(3). 得到 M M M 个回归问题决策树: f M ( x ) = ∑ m = 1 M T ( x ; θ m ) \begin{aligned}f_M(x)=\sum^M_{m=1}T(x;\theta_m)\end{aligned} fM(x)=m=1∑MT(x;θm)
完整示例1:
已知下表数据是训练数据集,有3个特征,年龄是要回归预测的值,只考虑使用回归树作为基函数,树的深度为1,回归树数量为2,学习这个回归树的提升模型。
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 年龄(年) | |
|---|---|---|---|---|
| x 1 x_1 x1 | 5000 | 7.5 | 165 | 19 |
| x 2 x_2 x2 | 5000 | 8.5 | 170 | 21 |
| x 3 x_3 x3 | 8000 | 7.5 | 170 | 29 |
| x 4 x_4 x4 | 8000 | 8.5 | 165 | 31 |
给定测试数据如下所示:
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 年龄(年) | |
|---|---|---|---|---|
| 测试1 | 5000 | 7 | 175 | ? |
按照GBDT算法,第一步确定损失函数以及残差:
L o s s F u n c t i o n = ( y − f m − 1 ( x ) ) 2 LossFunction=\begin{aligned}(y-f_{m-1}(x))^2\end{aligned} LossFunction=(y−fm−1(x))2
R e d u s i a l = 2 ( y i − f m − 1 ( x i ) ) Redusial=2(y_i-f_{m-1}(x_i)) Redusial=2(yi−fm−1(xi))
进入第二步,迭代提升阶段:
a) 求解划分点,枚举每一个特征及其阈值,使用平均方误差:
工资: 最小平均均方误差为1,划分为5000
| 划分点 | 小于等于划分点 | 大于划分点 | 左均值 | 右均值 | 平均方误差 |
|---|---|---|---|---|---|
| 5000 | x 1 , x 2 x_1,x_2 x1,x2 | x 3 , x 4 x_3,x_4 x3,x4 | 19 + 21 2 = 20 \frac{19+21}{2}=20 219+21=20 | 29 + 31 2 = 30 \frac{29+31}{2}=30 229+31=30 | ( 19 − 20 ) 2 + ( 21 − 20 ) 2 + ( 29 − 30 ) 2 + ( 31 − 30 ) 2 4 = 1 \frac{(19-20)^2+(21-20)^2+(29-30)^2+(31-30)^2}{4}=1 4(19−20)2+(21−20)2+(29−30)2+(31−30)2=1 |
| 8000 | x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4 | 无 | 19 + 21 + 29 + 31 4 = 25 \frac{19+21+29+31}{4}=25 419+21+29+31=25 | 无 | ( 19 − 25 ) 2 + ( 21 − 25 ) 2 + ( 29 − 25 ) 2 + ( 31 − 25 ) 2 4 = 26 \frac{(19-25)^2+(21-25)^2+(29-25)^2+(31-25)^2}{4}=26 4(19−25)2+(21−25)2+(29−25)2+(31−25)2=26 |
睡觉时间: 最小平均均方误差为25,划分为7.5
| 划分点 | 小于等于划分点 | 大于划分点 | 左均值 | 右均值 | 平均方误差 |
|---|---|---|---|---|---|
| 7.5 | x 1 , x 3 x_1,x_3 x1,x3 | x 2 , x 4 x_2,x_4 x2,x4 | 19 + 29 2 = 24 \frac{19+29}{2}=24 219+29=24 | 21 + 31 2 = 26 \frac{21+31}{2}=26 221+31=26 | ( 19 − 24 ) 2 + ( 21 − 26 ) 2 + ( 29 − 24 ) 2 + ( 31 − 26 ) 2 4 = 25 \frac{(19-24)^2+(21-26)^2+(29-24)^2+(31-26)^2}{4}=25 4(19−24)2+(21−26)2+(29−24)2+(31−26)2=25 |
| 8.5 | x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4 | 无 | 19 + 21 + 29 + 31 4 = 25 \frac{19+21+29+31}{4}=25 419+21+29+31=25 | 无 | ( 19 − 25 ) 2 + ( 21 − 25 ) 2 + ( 29 − 25 ) 2 + ( 31 − 25 ) 2 4 = 26 \frac{(19-25)^2+(21-25)^2+(29-25)^2+(31-25)^2}{4}=26 4(19−25)2+(21−25)2+(29−25)2+(31−25)2=26 |
身高: 最小平均均方误差为26,两种划分均可
| 划分点 | 小于等于划分点 | 大于划分点 | 左均值 | 右均值 | 平均方误差 |
|---|---|---|---|---|---|
| 165 | x 1 , x 4 x_1,x_4 x1,x4 | x 2 , x 3 x_2,x_3 x2,x3 | 19 + 31 2 = 25 \frac{19+31}{2}=25 219+31=25 | 21 + 29 2 = 25 \frac{21+29}{2}=25 221+29=25 | ( 19 − 25 ) 2 + ( 21 − 25 ) 2 + ( 29 − 25 ) 2 + ( 31 − 25 ) 2 4 = 26 \frac{(19-25)^2+(21-25)^2+(29-25)^2+(31-25)^2}{4}=26 4(19−25)2+(21−25)2+(29−25)2+(31−25)2=26 |
| 170 | x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4 | 无 | 19 + 21 + 29 + 31 4 = 25 \frac{19+21+29+31}{4}=25 419+21+29+31=25 | 无 | ( 19 − 25 ) 2 + ( 21 − 25 ) 2 + ( 29 − 25 ) 2 + ( 31 − 25 ) 2 4 = 26 \frac{(19-25)^2+(21-25)^2+(29-25)^2+(31-25)^2}{4}=26 4(19−25)2+(21−25)2+(29−25)2+(31−25)2=26 |
b) 拟合残差
按照GBDT算法,第一步求 f 1 ( x ) f_1(x) f1(x)即回归树 T 1 ( x ) T_1(x) T1(x),
针对“工资”这一特征的最佳切分点是5000,平均均方误差 ( 1 2 + 1 2 + 1 2 + 1 2 ) / 4 = 1 (1^2+1^2+1^2+1^2)/4=1 (12+12+12+12)/4=1。
“睡觉时间”特征的最佳切分点是7.5,平均均方误差 ( 5 2 + 5 2 + 5 2 + 5 2 ) / 4 = 25 (5^2 +5^2+5^2+5^2)/4=25 (52+52+52+52)/4=25。
“身高”特征的最佳切分点是170,平均平方误差 26 26 26。
因此, f 1 ( x ) f_1(x) f1(x) 最佳的特征选择是“工资”,切分点是5000.
T 1 ( x ) = { 20 , 工资 ≤ 5000 30 , 工资 > 5000 f 1 ( x ) = T 1 ( x ) T_1(x)=\begin{cases} 20,\ 工资\le 5000 \\ 30,\ 工资\gt 5000 \end{cases}\\ f_1(x)=T_1(x) T1(x)={20, 工资≤500030, 工资>5000f1(x)=T1(x)
用 f 1 ( x ) f_1(x) f1(x) 拟合训练数据的残差表如下所示, r 2 i = 2 × ( y i − f 1 ( x i ) ) , i = 1 , 2 , 3 , 4 r_{2i}=2\times(y_i-f_1(x_i)),\ i=1,2,3,4 r2i=2×(yi−f1(xi)), i=1,2,3,4。
| x i x_i xi | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 |
|---|---|---|---|---|
| r_{2i} | -2 | 2 | -2 | 2 |
残差替代了年龄标签去做后续的划分
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 残差 | |
|---|---|---|---|---|
| x 1 x_1 x1 | 5000 | 7.5 | 165 | -2 |
| x 2 x_2 x2 | 5000 | 8.5 | 170 | 2 |
| x 3 x_3 x3 | 8000 | 7.5 | 170 | -2 |
| x 4 x_4 x4 | 8000 | 8.5 | 165 | 2 |
第二步求 T 2 ( x ) T_2(x) T2(x)。方法与求 T 1 ( x ) T_1(x) T1(x)一样,只不过是拟合上表中的残差,可以得到:
T 2 ( x ) = { − 2 , 睡觉时间 ≤ 7.5 2 , 睡觉时间 > 7.5 T_2(x)=\begin{cases} -2,\ 睡觉时间\le 7.5 \\ 2,\ 睡觉时间\gt 7.5 \end{cases} T2(x)={−2, 睡觉时间≤7.52, 睡觉时间>7.5
对于上面的公式,这里特征选择睡觉时间比身高好,区间划分则以7.5为划分区间,比8.5要好。小于等于7.5为 x 1 , x 3 x_1, x_3 x1,x3,大于7.5为 x 2 , x 4 x_2, x_4 x2,x4。值为平均值。
再来看下面公式的结果, T 2 ( x ) T_2(x) T2(x)是这一步求出来的树模型结果。 f i ( x ) f_i(x) fi(x)是前面 i i i个树模型综合结果,在这里 i = 1 i=1 i=1,前面只有一个树模型,所以 f 1 ( x ) = T 1 ( x ) f_1(x)=T_1(x) f1(x)=T1(x)。 T 1 ( x ) T_1(x) T1(x)与 T 2 ( x ) T_2(x) T2(x)两个树的结果进行相加综合,结果因为条件融合而被进一步划分,得到如下所示的结果:
使用公式: f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) f_m(x)=f_{m-1}(x)+T(x;\theta_m) fm(x)=fm−1(x)+T(x;θm)
f 2 ( x ) = f 1 ( x ) + T 2 ( x ) = 20 − 2 = 18 f_2(x) = f_1(x)+T_2(x)=20-2=18 f2(x)=f1(x)+T2(x)=20−2=18
f 2 ( x ) = f 1 ( x ) + T 2 ( x ) = 20 + 2 = 22 f_2(x) = f_1(x)+T_2(x)=20+2=22 f2(x)=f1(x)+T2(x)=20+2=22
f 2 ( x ) = f 1 ( x ) + T 2 ( x ) = 30 − 2 = 28 f_2(x) = f_1(x)+T_2(x)=30-2=28 f2(x)=f1(x)+T2(x)=30−2=28
f 2 ( x ) = f 1 ( x ) + T 2 ( x ) = 30 + 2 = 32 f_2(x) = f_1(x)+T_2(x)=30+2=32 f2(x)=f1(x)+T2(x)=30+2=32
结果为回归树叶子节点预测值的累加。
f 2 ( x ) = f 1 ( x ) + T 2 ( x ) = { 18 , 工资 ≤ 5000 睡觉时间 ≤ 7.5 h 22 , 工资 ≤ 5000 睡觉时间 > 7.5 h 28 , 工资 > 5000 睡觉时间 ≤ 7.5 h 32 , 工资 > 5000 睡觉时间 > 7.5 h f_2(x)=f_1(x)+T_2(x)=\begin{cases} 18,\ 工资\le 5000\ 睡觉时间\le7.5h \\ 22,\ 工资\le 5000\ 睡觉时间\gt7.5h \\ 28,\ 工资\gt 5000\ 睡觉时间\le7.5h \\ 32,\ 工资\gt 5000\ 睡觉时间\gt7.5h \\ \end{cases} f2(x)=f1(x)+T2(x)=⎩ ⎨ ⎧18, 工资≤5000 睡觉时间≤7.5h22, 工资≤5000 睡觉时间>7.5h28, 工资>5000 睡觉时间≤7.5h32, 工资>5000 睡觉时间>7.5h
用 f 2 f_2 f2 拟合训练数据的平方损失误差是:
L ( y , f 2 ( x ) ) = ∑ i = 1 4 ( y i − f 2 ( x i ) ) 2 = ( 19 − 18 ) 2 + ( 21 − 22 ) 2 + ( 28 − 29 ) + ( 31 − 32 ) = 4 \begin{aligned}L(y,f_2(x)) &=\sum^4_{i=1}(y_i-f_2(x_i))^2\\&=(19-18)^2+(21-22)^2+(28-29)+(31-32)\\&=4\end{aligned} L(y,f2(x))=i=1∑4(yi−f2(xi))2=(19−18)2+(21−22)2+(28−29)+(31−32)=4
因为此时已经满足条件(回归树的数量),那么 f ( x ) = f 2 ( x ) f(x)=f_2(x) f(x)=f2(x)记为所求的提升树。
使用 f ( x ) f(x) f(x)对测试1的预测值是18,如下所示:
| 工资(元/月) | 睡觉时间(小时/天) | 身高(cm) | 年龄(年) | |
|---|---|---|---|---|
| 测试1 | 5000 | 7 | 175 | 18 |
Gradient Boosting In Depth Intuition- Part 1 Machine Learning (Youtube)
Gradient Boosting Decision Tree Algorithm Explained (Youtube)
GBDT内容介绍 (Youtube)
三、GBDT的应用
1、GBDT 函数参数与方法
具体参数与方法可参考:
GradientBoostingClassifier (scikit)
GradientBoostingRegressor(scikit)
下面列举常用的参数与方法:
from sklearn.ensemble import GradientBoostingClassifier, GradientBoostingRegressor
GradientBoostingClassifier()
GradientBoostingRegressor()
| 参数 | 默认 | 说明 |
|---|---|---|
| loss | 回归squared_error/分类deviance | 用于指定GBDT算法的损失函数,对于分类的GBDT可选’deviance’和’exponential’,分别表示对数似然损失函数和指数损失函数;对于预测的GBDT,可以选择’ls’,‘lad’,'huber’和‘quantile’,分别表示平方损失函数、绝对损失函数、Huber损失函数(前两种损失函数的结合,当误差较小时,使用平方损失,否则使用绝对值损失,误差大小的度量可使用alpha参数指定)和分位数回归损失函数(需通过alpha参数设定分位数) |
| learning_rate | 0.1 | 用于指定模型迭代的学习率或步长,即对应的梯度提升模型 F ( x ) F(x) F(x) 可以表示为 F M ( x ) = F M − 1 ( x ) + v f m ( x ) F_M(x)=F_{M-1}(x)+vf_m(x) FM(x)=FM−1(x)+vfm(x),其中 v v v 就是学习率。对于较小的学习率 v v v而言,则需要迭代更多次的基础分类器,通常情况下需要利用较差验证法确定合理的基础模型的个数和学习率 |
| n_estimators | 100 | 用于指定基础模型的数量 |
| max_depth | 3 | 每个基础模型最大深度 |
| max_features | None | 每次分裂时考虑多少特征,默认考虑所有 |
| random_state | None | 随机种子 |
2、案例:推荐系统预测模型 GBDT+LR
2.1、背景介绍
Facebook是一款非常著名的社交软件,它的公司想通过用户的某一个使用习惯: 用户的点击率CTR(click through rate)喜欢就点击而不喜欢就忽略,从而去更加的了解用户的喜好,进而能够定向推荐,为公司带来更多收益。
问题一:样本数量大,点击率预估模型中的训练样本可达上亿级别。
很明显,预测用户是否点击,这是个二分类问题,点或者不点,那么分类问题会有非常多的模型可选,决策树,LR,SVM等等。
为了解决数据量过大的问题,所以直接采用了线性模型LR,速度快,参数量少,处理起来效率非常高。
问题二:学习能力有限。
速度虽然快了,但是局限于LR模型的简单,大量数据的关键特征没有被利用起来,很多隐含信息没有充分使用,这是一种非常大的损失。
既然如此,我们就去帮LR提取特征特征再喂给它,如何提取呢?人工提取或者机器自动提取。
问题三:人工成本高。
使用人工方式找到有区分度的特征或者特征组合很有难度:
- 对人要求高。它对人的经验要求非常高,如何辨别特征的重要程度,以及如何根据需求从现有特征生成新特征都具有挑战。
- 时间成本高。人的思考需要时间,对于复杂特征更是如此,所以这是一项耗时的过程。
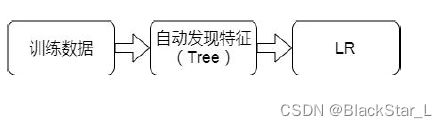
既然如此,我们就需要使用机器去自动学习,去发现有效特征以及特征组合,去代替人工,弥补人工经验不足,缩短LR试验周期。

解决方案:
我们需要选出更具有关联的特征,这里选择了GBDT这种boosting算法,它是将分类正确的特征赋予
2.2、深入了解
GBDT+LR 是一种具有stacking思想的二分类器模型,用来解决二分类问题。这个方法出自于Facebook 2014年的论文 Practical Lessons from Predicting Clicks on Ads at Facebook 。
这个思想最经典的莫过于下面这张图了,可以看出它由两部分组成,红色框代表着GBDT,绿色框代表着LR模型,他们拼接在一起也就是stacking思想。看起来复杂,然而代码实现上实际就是两个模型按照顺序执行,先通过GBDT将特征进行组合,然后传入给LR线性分类器,即下一个模型使用上一个模型的结果。最后,LR对GBDT产生的输入数据进行分类(使用L1正则化防止过拟合)。
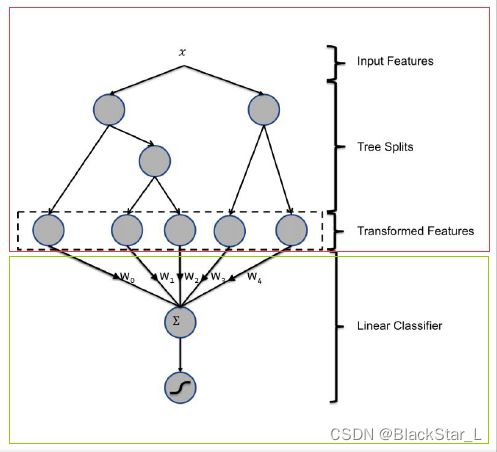
我们再来回顾下GBDT的概念:
- 回归树 Regression Decision Tree
GBDT由多棵CART回归树组成,将累加所有树的结果作为最终结果
GBDT拟合的目标是一个梯度值(连续值,实数),所以在GBDT里,都是回归树。
GBDT用来做回归预测,调整后也可以用于分类 - 梯度迭代 Gradient Boosting
Boosting,迭代,即通过迭代多棵树来共同决策
损失函数用于评价模型性能(一般为拟合程度+正则项)。最好的方法就是让损失函数沿着梯度方向下降
Gradient Boosting,每一次建立模型是在之前模型损失函数的梯度下降方向 - GBDT(Gradient Boosting Decision Tree) 是将所有树的结果累加起来,最终的结果为:第一棵树的预测值+之后每一棵树学的之前所有树结果和的残差。
- 首先我们需要训练模型,我们将训练集输入GBDT模型中进行训练,如图上红色大框框,训练过程采用boosting算法,从最重要的特征开始,每个特征为一棵树模型,如图tree1和tree2,分别对两个不同特征构建决策树,同样使用残差对树进行拟合,第一棵树的残差会作为第二棵树的输入,最后都会生成叶子节点预测值。
- GBDT预测出结果后,需要做一步处理,即输出的并不是最终的二分类概率值,而是要把模型中的每棵树计算得到的预测概率值所属的叶子节点位置记为1,其他叶子记为0。每棵树的结果拼到一起构成新的训练数据。
- 如图:如果一个实例,选择了第一棵决策树的第2个叶子节点。同时,选择第2棵子树的第1个叶子节点。那么前3个叶子节点中,第2 位设置为1 , 后2 个叶子节点中, 第1 位设置为1 。concatenate所有特征向量,得到[0,1,0,1,0]。
GBDT是一堆树的组合,假设有 k k k棵树 ( T 1 , T 2 . . . T k ) (T_1,T_2...T_k) (T1,T2...Tk),每棵树的节点数分别为 N i N_i Ni,GBDT会输出一个 ∑ i = 1 k N i \begin{aligned}\sum^k_{i=1}N_i\end{aligned} i=1∑kNi维的向量 X g b d t X_{gbdt} Xgbdt - 结果传入到LR模型进一步训练(注意GBDT和LR不是且不能并行训练,它们有前后的逻辑关系),得到最终的二分类结果。(当然也可以多分类)
2.3、算法Demo演示
GBDT+LR算法Demo演示
随机生成二分类样本8万个,每个样本20个特征
采用RF,RF+LR,GBDT,GBDT+LR进行二分类预测
# 随机种子,复现下面随机生成的分类问题数据集
import numpy as np
np.random.seed(10)
# 随机创建分类问题数据集
from sklearn.datasets import make_classification
# 线性模型,逻辑回归
from sklearn.linear_model import LogisticRegression
# 集成模型,梯度提升分类器
from sklearn.ensemble import GradientBoostingClassifier
# 切分数据集为训练集与测试集
from sklearn.model_selection import train_test_split
# 独热编码,使GBDT产生新特征
from sklearn.preprocessing import OneHotEncoder
生成分类数据集,在进行划分,后40000当做测试集,前40000当做训练集,对于训练集,再取一半20000当做GBDT的训练集,另一半当做LR的训练集:
X, y = make_classification(n_samples=80000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
X_train, X_train_lr, y_train, y_train_lr = train_test_split(X_train, y_train, test_size=0.5)
拟合GBDT模型,寻找每棵树的叶子节点索引,即分类的类型:
# 拟合GBDT模型
grd = GradientBoostingClassifier(n_estimators=10)
grd.fit(X_train, y_train)
"""
重点:
apply与predict相同之处是都可以输出预测,但是predict输出预测值,而apply将预测结果转变成子叶索引。
apply(X_train):X_train的每个样本通过GBDT模型预测出结果(某个子叶),再寻找该结果(子叶)的索引
"""
indexes = grd.apply(X_train)
下面对indexes进行讲解:
查看indexes的结构,三维数组,数字从外到内看,最外层有20000个二维数组,表示的是样本数量X_train;再进一层10表示的是基生成器(子树个数),每个样本要跑最多10个基生成器综合结果,最后一个1表示的是样本在每棵树的结果 (二分类只有一个结果,而多分类可能有对应的多个结果,最后一层内部元素数量就会大于1),使用apply则表示该样本在每棵树上的结果子叶索引。

indexes结果如下:

截取一部分做讲解,下图中,每个红色框的部分为一个样本,后面一共会有2w个;n_estimators设置为10,则红框内的二维数组内的一维数组有10个,表示10基生成器,即对应10个子叶结果索引,[13],[11],[14] 等等表示的就是索引。

对于多维数组的索引[, …, …, ] 每一个逗号分割不同维度,从左到右维度从外向内,从高到低。第一个 : 选取所有样本,第二个 : 选取所有基生成器,最后一个 0 表示选取基生成器的结果的第一个值,即13,14,11,3等等索引,选取后维度降低一阶,在这里就是直接把最内一层[13],[14],…,[11],[3]等等合并为[13,14,…,11, 3]。
可以举个例子:
import numpy as np
a = np.array([[1], [2]. [3]])
print(a[:,0]) # 结果为 array([1, 2, 3]),注意列表无此操作
这一步的意思就是把每个样本对应的10个基生成器的结果合并在一起
indexes_combination = indexes[:,:,0]
结果如下,变成了二维数组,每一行表示每个样本的结果子叶索引,每一列表示不同样本在同一棵树(特征)上的结果(特征值)。
为了更好地与后面的LR模型结合,所以使用OneHot编码去构造新特征,这样不仅仅使距离距离的计算更加合理(比如13,3,11之间实际上代表类别是等距的),而且而one-hot后有更多权值管理了这个特征,这样使得参数管理的更加精细,也就拓展了LR模型的非线性能力,详情可以参考:关于One-hot编码的一些整理及用途[转载+整理]
所以,接下来进行OneHot编码:
具体OneHotEncoder的使用可以参考:OneHotEncoder函数
# 生成模型类,便于复用
grd_enc = OneHotEncoder(categories='auto')
"""
将OneHot编码运用到训练好的GBDT的结果上
当使用GBDT测试新的结果时,转换为子叶索引喂给OneHotEncoder模型,会自动将结果进行OneHot编码,转换成0/1
"""
grd_enc.fit(indexes_combination)
# grd_enc.get_feature_names() # 查看每一列对应的特征
创建逻辑回归模型,并进行训练:
# 创建模型类
# max_iter=1000 模型求解最大迭代次数
# solver = 'lbfgs' 拟牛顿法
grd_lm = LogisticRegression(solver='lbfgs', max_iter=1000)
"""
输入LR的训练数据,训练数据即X_train_lr在GBDT内的子叶索引,再进行OneHot编码后的0/1样本集
X_train 训练一遍GBDT生成模型(能产生新特征的模型),X_train_lr 通过GBDT生成新数据再经过LR更好的训练,生成LR模型(在新特征上的、效果更好的模型)
"""
grd_lm.fit(grd_enc.transform(grd.apply(X_train_lr)[:,:,0]), y_train_lr)
最后一步,开始使用测试集预测结果,再对结果进行评价:
y_pred_grd_lm = grd_lm.predict_proba(grd_enc.transform(grd.apply(X_test)[:, :, 0]))[:,1]
predict_proba函数把每个样本的针对每个分类结果的预测概率求解出来:
该样本时二分类,两列,每一列表示两种不同分类标签,值为属于该类标签的概率,这里取了第二列作为评估标准。
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred_grd_lm)
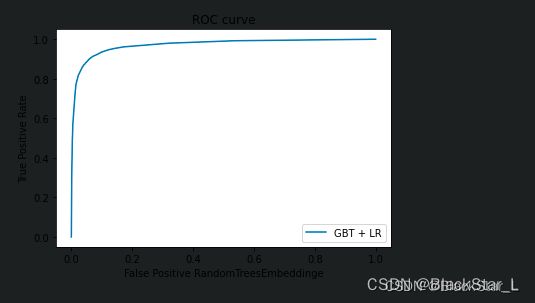
绘制ROC(receiver operating characteristic curve - 受试者工作特征曲线)曲线,AUC(Area Under Curve) 面积越大,说明模型效果越好:
import matplotlib.pyplot as plt
plt.figure(3)
plt.plot(fpr_grd_lm, tpr_grd_lm, label='GBT + LR')
plt.xlabel('False Positive RandomTreesEmbeddinge')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()
参考
微分,梯度及梯度下降法(csdn)
Gradient Boosting In Depth Intuition- Part 1 Machine Learning (Youtube)
Gradient Boosting Decision Tree Algorithm Explained (Youtube)
GBDT内容介绍 (Youtube)
GradientBoostingClassifier (scikit)
GradientBoostingRegressor(scikit)
Greedy function Approximation – A Gradient Boosting Machine
Practical Lessons from Predicting Clicks on Ads at Facebook
关于One-hot编码的一些整理及用途[转载+整理]
OneHotEncoder函数
更新时间
2022/01/29
2022/10/22
2022/10/25