Python实现经典机器学习案例 良/恶性性乳腺癌肿瘤预测

Python实现经典机器学习案例 良/恶性性乳腺癌肿瘤预测

首先给出数据下载地址
http://note.youdao.com/groupshare/?token=C6B145FA919F41F8ACAAC39EE775441C&gid=93772390

数据可视化

画出一张以肿块厚度为横坐标，以细胞尺寸为纵坐标的，肿瘤阴阳性类型的散点图

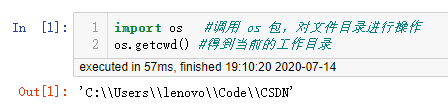
查看工作目录

import os   #调用 os 包，对文件目录进行操作
os.getcwd() #得到当前的工作目录

找到工作目录所在位置，并将数据复制到该目录下

读取数据

#导入 pandas （针对数据处理分析的包，用于实现数据读写，清洗，填充以及分析功能，节省数据预处理的时间），并且更名为 pd
import pandas as pd
#调用 pandas 工具包的 read_csv 函数，传入地址参数，返回数据并且存至变量 df_train
df_train=pd.read_csv('breast-cancer-train.csv') 
#调用 pandas 工具包的 read_csv 函数，传入地址参数，返回数据并且存至变量 df_test
df_test=pd.read_csv('breast-cancer-test.csv')
#查看pana数据类型，实际上是一个 pandas 核心的数据框（ DataFrame ）
type(df_train) 

查看数据基本情况

#查看这个数据框有多少行多少列，524 行（即 524 个患者）4 列（ 4 个变量名）
df_train.shape

查看前五行数据

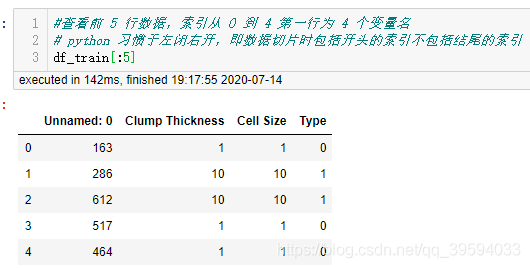
#查看前 5 行数据，索引从 0 到 4 第一行为 4 个变量名
# python 习惯于左闭右开，即数据切片时包括开头的索引不包括结尾的索引
df_train[:5]

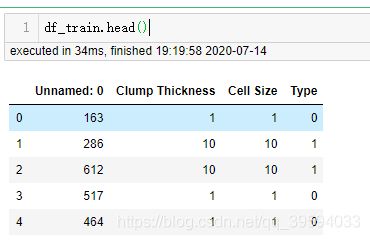
df_train.head()

切片：可从数据框中提取数据（包括行、列以及行和列）。

loc 方法：提取数据框中部分数据的方法为“数据集名.loc[ ] ”

可将提取的部分数据重新定义为数据集，方便查看和使用。

总结：切片可以用数据集名称选取所需行（多行）或者列（一列），也可以通过数据集名称加“.loc”来更细化的选择数据,这时行与行之间通过“：”隔开，行与列之间先用逗号隔开，所选列用“[]”括起来，列名用“’’”,列与列值间用逗号隔开。

# pandas 包的切片函数 数据框.loc[取行的条件，取列的条件]，
# 这两步命令主要意思是在 df_test 数据框中选出 Type 为 0 的 Clump Thickness 和 Cell Size 值，
# 组成一个数据框并且存至 df_test_negative 变量，同样 Type 为 1 的存入 df_test_positive 变量，分别表示阴性和阳性

df_test_negative = df_test.loc[df_test['Type'] == 0][['Clump Thickness', 'Cell Size']]
df_test_positive = df_test.loc[df_test['Type'] == 1][['Clump Thickness', 'Cell Size']]

#导入 matplotlib 包中的 pyplot 函数，并更名为 plt
import matplotlib.pyplot as plt 
#画出 阴性的散点图，以‘ o ’为标记，大小 200 ，颜色为红色
plt.scatter(df_test_negative['Clump Thickness'],df_test_negative['Cell Size'], marker = 'o', s=200, c='red')
#画出 阳性的散点图，以‘ x ’为标记，大小 150 ，颜色为黑色
plt.scatter(df_test_positive['Clump Thickness'],df_test_positive['Cell Size'], marker = 'x', s=150, c='black')

#用法：plt.scatter(数据集名['列名（横坐标）'],数据集名['列名（横坐标）'], marker = ' （记号）', s=（大小）, c='颜色')
#设置行标签为 Clump Thickness
plt.xlabel('Clump Thickness')
#设置列标签为 Cell Size
plt.ylabel('Cell Size')
#显示图
plt.show() 

我们可以看到，恶性肿瘤大多位于图的右上方，良性肿瘤大多位于图的左下方。

随机生成一个线性分类器

#导入 numpy 包（主要用其中的 random 函数产生随机数），并且更名为 mp
import numpy as np 

# 设置随机种子为 0 以确保每次运行结果一致
np.random.seed(0)
#用 random 函数产生一个随机数并存入 intercept 变量，作为直线截距
intercept = np.random.random([1]) 
#用 random 函数产生两个随机数并存入 coef 变量，作为系数
coef = np.random.random([2])      

#打印出这个随机数
print(intercept)

#产生一个 0 到 11 ，即 0 ...11的序列存入 lx
lx = np.arange(0, 12)   
#利用随机生成的 intercept coef[0] coef[1] 计算 ly,  coef[0]x+coef[1]y=intercept
ly = (-intercept - lx * coef[0]) / coef[1]

#利用 plt 函数画出这条直线，其中 lx 为横坐标，ly 为纵坐标，颜色为黄色
plt.plot(lx, ly, c='yellow')


#画出 阴性的散点图，以‘ o ’为标记，大小 200 ，颜色为红色
plt.scatter(df_test_negative['Clump Thickness'],df_test_negative['Cell Size'], marker = 'o', s=200, c='red')
#画出 阳性的散点图，以‘ x ’为标记，大小 150 ，颜色为黑色
plt.scatter(df_test_positive['Clump Thickness'],df_test_positive['Cell Size'], marker = 'x', s=150, c='black')

#用法：plt.scatter(数据集名['列名（横坐标）'],数据集名['列名（横坐标）'], marker = ' （记号）', s=（大小）, c='颜色')
#设置行标签为 Clump Thickness
plt.xlabel('Clump Thickness')
#设置列标签为 Cell Size
plt.ylabel('Cell Size')
#显示图
plt.show()  

我们可以看到没有经过学习的初始化随机分类器，分类效果很糟糕。

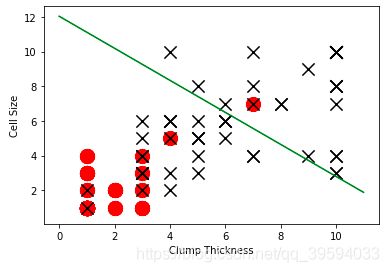
使用 10 条训练数据，训练一个 logistic 回归分类器

# 从 sklearn 的 线性模型中 导入逻辑回归模块
from sklearn.linear_model import LogisticRegression
# 初始化一个 Logistic 回归，类
lr = LogisticRegression()


# lr.fit:根据已有数据，训练出回归模型
# lr.fit调用格式：lr.fit(自变量（矩阵)，因变量)
lr.fit(
df_train[['Clump Thickness', 'Cell Size']][:10],#自变量：训练集的前十行的 'Clump Thickness'与 'Cell Size' 两列
df_train['Type'][:10]#因变量：训练集前10行的 'Type'
)
#lr.score:将训练出的 lr 模型应用于指定数据，返回正确率
print ('Testing accuracy (10 training samples):', lr.score(df_test[['Clump Thickness', 'Cell Size']], df_test['Type']))

对测试集数据分类准确率达到83%。
绘图

#返回 lr 模型的截距;一个只包含一个数的 array
intercept = lr.intercept_
#返回 lr 模型的斜率；包含两个数的 array
coef = lr.coef_[0, :]

#产生一个 0 到 11 ，即 0 ...11的序列存入 lx
lx0 = np.arange(0, 12)   
#利用 intercept coef[0] coef[1] 计算 ly,  coef[0]x+coef[1]y=intercept
# 给出线性模型表达式
ly = (-intercept - lx0 * coef[0]) / coef[1]

# 绘制分类器超平面
plt.plot(lx0, ly, c='green')

##画出 阴性的散点图，以‘ o ’为标记，大小 200 ，颜色为红色
plt.scatter(df_test_negative['Clump Thickness'],df_test_negative['Cell Size'], marker = 'o', s=200, c='red')
#画出 阳性的散点图，以‘ x ’为标记，大小 150 ，颜色为黑色
plt.scatter(df_test_positive['Clump Thickness'],df_test_positive['Cell Size'], marker = 'x', s=150, c='black')

#用法：plt.scatter(数据集名['列名（横坐标）'],数据集名['列名（横坐标）'], marker = ' （记号）', s=（大小）, c='颜色')
#设置行标签为 Clump Thickness
plt.xlabel('Clump Thickness')
#设置列标签为 Cell Size
plt.ylabel('Cell Size')
#显示图
plt.show()  

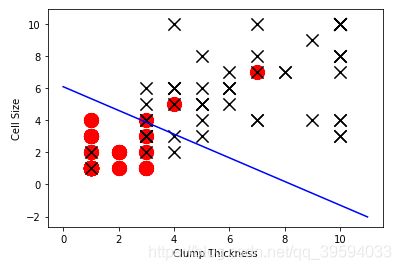
使用所有训练数据，训练一个 logistic 回归分类器

lr = LogisticRegression()

lr.fit(df_train[['Clump Thickness', 'Cell Size']], df_train['Type'])
print( 'Testing accuracy (all training samples):', lr.score(df_test[['Clump Thickness', 'Cell Size']], df_test['Type']))

对测试集数据分类准确率达到93%。

绘图

intercept = lr.intercept_
coef = lr.coef_[0, :]

#输出回归方程的截距与系数
print (intercept)
print (coef)

ly = (-intercept - lx0 * coef[0]) / coef[1]

plt.plot(lx0, ly, c='blue')
plt.scatter(df_test_negative['Clump Thickness'],df_test_negative['Cell Size'], marker = 'o', s=200, c='red')
plt.scatter(df_test_positive['Clump Thickness'],df_test_positive['Cell Size'], marker = 'x', s=150, c='black')
plt.xlabel('Clump Thickness')
plt.ylabel('Cell Size')
plt.show()

参考

范淼，李超.Python 机器学习及实践[M].清华大学出版社, 北京, 2016.