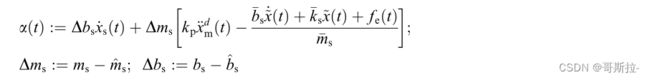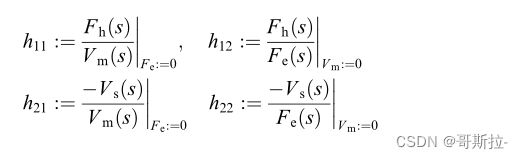（主从-阻抗）论文阅读笔记2

Stable bilateral teleoperation under a time delay using a robust impedance control（Q2）

This paper presents a new impedance controller for a bilateral teleoperation under a time delay
1.主从机器人都设计有阻抗控制器 (主端易于拖动，从端为了跟踪力和位置时柔顺交互)
2.为了解决从机的不确定性，将阻抗模型引入滑模控制的滑模面（从机有什么不确定性，将阻抗模型引入滑模面是什么操作）
3.从绝对稳定性概念推导了一个稳定条件，并据此提出了一种参数整定算法（？？，调整什么的参数）

1.引言

机器人任务中：
与环境过度的接触力应该被预防
自由运动时良好的跟踪性也很重要
阻抗控制适用于这些连续地受限和不确定的遥操作任务

引言里介绍的论文挺有用的有空可以看看

这篇论文对于时延遥操作系统提出了一种鲁棒阻抗控制方法，基于期望模型和滑模控制，设计了鲁棒阻抗控制器，并推导了系统的稳定性

2.模型定义

针对单自由度主从系统，总结了控制器设计中使用的一些定义。
动力学：
$$m_m{\ddot{x}}_m(t)+b_m{\dot{x}}_m(t)=u_m(t)+f_h(t)\text{\hspace{1em}(1)}$$
$$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_s(t)+f_e(t)\text{\hspace{1em}(2)}$$

$x_s=k_p{x}_m^d$

$f_h=k_f{f}_e^d$

$k_p$ 和 $k_f$ 是比例因子

3. 控制器设计

3.1. 主机器人阻抗控制器设计（计算力矩法）

主机器人的期望阻抗特性为：
$${\bar{m}}_m{\ddot{x}}_m(t)+{\bar{b}}_m{\dot{x}}_m(t)+{\bar{k}}_m{x}_m(t)=f_h(t)-k_f{f}_e^d(t)\text{\hspace{1em}(3)}$$
${\bar{m}}_m、{\bar{b}}_m、{\bar{k}}_m$为期望阻抗参数，为主机的可操作性性而选择（换言之，方便拖动，这不是和田老师说的一样吗，这种方法无透明性可言吧，始终能感受到到工具的存在,这情况 $k_m$ 是等于 0 吧，毕竟我想任意拖动，而不是位置跟踪）
联立（1）（3），可以消去 ${\ddot{x}}_m(t)$ 或者 $f_h(t)$ 都比较难,一个得外力估计，一个噪声很大

3.2. 从机基于滑模控制的阻抗控制器设计

在从机控制中，自由空间中的跟踪性能和从机的接触稳定性受到所需阻抗模型的影响，从机器人期望的阻抗特性为：
$${\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)=-f_e(t)\text{\hspace{1em}(4)}$$
其中
$$\tilde{x}(t)=x_s(t)-k_p{x}_m^d(t)$$

它使用了滑模控制的鲁棒特性，以应对参数不确定性和未建模动力学等不确定性

$u_{s1}(t)=({\hat{b}}_s-\frac{{\hat{m}}_s}{{\bar{m}}_s}{\bar{b}}_s){\dot{x}}_s(t)-\frac{{\hat{m}}_s}{{\bar{m}}_s}{\bar{k}}_s{x}_s(t)+{\hat{m}}_s{k}_p(\frac{{\bar{b}}_s}{{\bar{m}}_s}-\frac{{\bar{b}}_m}{{\bar{m}}_m}){\dot{x}}_m^d(t)+{\hat{m}}_s{k}_p(\frac{{\bar{k}}_s}{{\bar{m}}_s}-\frac{{\bar{k}}_m}{{\bar{m}}_m})x_m^d(t)+\frac{{\hat{m}}_s}{{\bar{m}}_s}{k}_p{f}_h^d(t)+\frac{{\bar{m}}_m-{\hat{m}}_s}{{\bar{m}}_m}{f}_e(t)-\frac{{\hat{m}}_s}{{\bar{m}}_m}{k}_p{k}_f{f}_e^{dd}(t)$

? ?论文提到这个控制器设计于另一篇会议（IROS）论文
Impedance Controller Design of Internet-Based Teleoperation Using Absolute Stability Concept,但是下文还是对这个公式做了一个推导

从机动力学：
$$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_s(t)-f_e(t)$$

期望阻抗模型：
$${\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)=-f_e(t)$$
$$\tilde{x}=x_s(t)-k_p{x}_m^d(t)$$
为了实现该阻抗特性设计滑模面：
$$I_e(t)={\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)-(-f_e(t))$$
$$s=\frac{1}{{\bar{m}}_s}{\int }_0^t{I}_e(\tau )d\tau =\dot{\tilde{x}}(t)+\frac{{\bar{b}}_s}{{\bar{m}}_s}\tilde{x}(t)+\frac{1}{{\bar{m}}_s}{\int }_0^t[{\bar{k}}_s\tilde{x}(\tau )+f_e(\tau )]d\tau$$
$$\dot{s}=\ddot{\tilde{x}}(t)+\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)]$$
当系统处于滑模面上时，$\dot{s}=0$
从机动力学：
$$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_s(t)-f_e(t)$$
$${\ddot{x}}_s(t)-k_p{\ddot{x}}_m^d(t)=-(\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)])$$
联立得(直接$\dot{s}=0$,和计算力矩的不同在于联立的期望模型是impedance error )：
$$\begin{array}{rl}{u}_{eq}(t)& ={\hat{m}}_s(-(\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)]))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)\\ & =\frac{{\hat{m}}_s}{{\bar{m}}_s}({\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)\end{array}$$

$${\bar{m}}_m{\ddot{x}}_m(t)+{\bar{b}}_m{\dot{x}}_m(t)+{\bar{k}}_m{x}_m(t)=f_h(t)-k_f{f}_e^d(t)\text{\hspace{1em}(3)}$$
实际我们当然不能直接带，引入a discontinuous term，保证s收敛到0，并且利用3式对 ${\ddot{x}}_m^d$ 进行降阶
$$u_{s2}(t)=u_{eq}(t)-K_{g}sat(\frac{s(t)}{\Phi })$$

4. 稳定性分析

4.0 无源性绝对稳定性知识补充（没有写完）

4.0.0 前言

Q1 无源性、绝对稳定性是用来干嘛的
一个双端口网络的模型，其稳定性可以由绝对稳定性和无源性两种方法来保证。 无源性是绝对稳定性的充分非必要条件，即无源的系统一定绝对稳定，反之不成立，无源双边控制算法稳定性的鲁棒性很强，在任何时延条件下都能保证系统稳定，但系统的操作性能较差。用绝对稳定性代替无源性作为时延力反馈系统的稳定判据，可以减少稳定性与透明性的冲突，取得更好的操作性能。

Q2、无源性定义及判据
无源性分析
无源系统的理解
浅谈无源性理论在协作机器人上的应用
无源器件：电阻，电容和电感这种只能自身消耗或不产生能量的元器件称为无源器件

无源和稳定是如何联系起来的？
以下是无源控制理论及其应用书本内容加些自己理解吧！

4.0.1 耗散性与无源性

耗散性（dissipativity）是与系统能量损失或者耗散现象紧密相关物理系统的基本性质。典型的耗散系统的例子是电路，电路中的部分电能和磁场能在电阻中以热的形式耗散。在机械系统中摩擦起到类似作用。
要精确地定义耗散性，需要引入两个函数：一是供给率反映流入系统能量的速率，及供给率（supply rate）;而是测量存入系统能量的储存函数 (storage function)，这些函数通过耗散不等式联系在一起。耗散不等式即：沿着耗散系统的时间轨迹，供给率不少于能量存储的增加。这就表示耗散系统存储的能量不能多于外界供给的能量。（率和量要做比较肯定有一个率积分吧）
例如rlc电路：

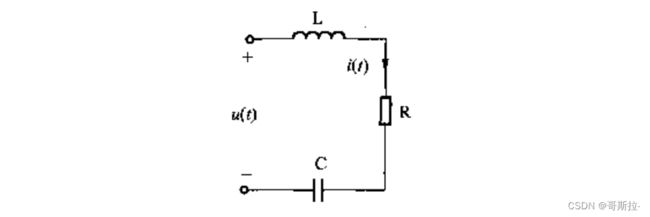
根据基尔霍夫定律得到电路的动态方程：
$$u=Ri+\frac{1}{C}{\int }_0^{t}i(\tau )d\tau +L\frac{di}{dt}$$
式两边乘i可得：
$$ui=R{i}^2+\frac{1}{C}i{\int }_0^{t}i(\tau )d\tau +Li\frac{di}{dt}$$
等效为：

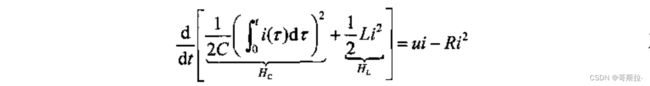
供给率函数 $ui$ 是外部电源向电路的输入功率，而储存函数 $H=H_c+H_l$ 是系统的总能量，上式表明：沿着耗散系统的时间轨迹，供给率不少于能量存储的增加
对上式积分得：

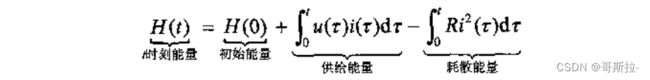
上式表明：耗散系统存储的能量不能多于外界供给的能量
如果把u作为输入，i作为输出y，则认为系统是无源的，那么系统和系统的稳定性有什么关系呢？如何联系起来

4.0.2 微分几何

4.0.2.1 非线性坐标变换与微分同胚

非线性坐标变换可表示为：
$$z=\varphi (x)$$
式中，z为与x同维的向量，$\varphi$为非线性函数向量。
上式的逆变换为：
$$x={\varphi }^{-1}(x)$$

4.0.2.1 李导数

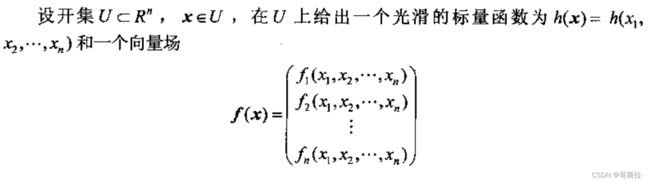
根据h(x)和f(x)定义一个新的标量函数，记做$L_{f}h(x)$有：
$$L_{f}h(x)=<\frac{\partial h(x)}{\partial x_i},f(x)>=\sum _i^n\frac{\partial h(x)}{\partial x_i}{f}_i(x)$$

4.0.3 系统的耗散性与无源性定义

考虑多输入多输出系统：
$$S:\{\begin{array}{ll}\dot{x}=f(x,u),& \\ y=h(x),& x(0)=x_0\in R^n\end{array}\text{\hspace{1em}(5)}$$
式中，$x\in R^n$,$u\in R^m$为输入；$y\in R^m$为输出，是关于x连续的
定义耗散性：当且仅当存在存储函数 $H：R^n\to R\ge 0$有
$$H[x(T)]\le H[x(0)]+{\int }_0^{T}w[u(\tau )，y(\tau )]d\tau$$
则系统相对于供给率 $w[u,y]$ 是耗散的
定义无源性：当系统是耗散的，且供给率 $w(u,y)=u^{T}y$,则 系统 是无源的。显然，无源性是耗散性的特例。如果系统是耗散的。且 $w(u,y)=u^{T}y-{\delta }_i||u|{|}^2$（${\delta }_i$为输入严格无源度，${\delta }_i>0$）,则系统是输入严格无源的。同理，如果系统是耗散的，且$w(u,y)=u^{T}y-{\delta }_0||y|{|}^2$（${\delta }_0$为输入严格无源度，${\delta }_0>0$）,则S是输出严格无源的
更具体来讲，标量函数$L_{f}H(x)$表示函数$H(x)$沿着向量场$f(x)$的导数，对于系统(5),如果存在连续可微半正定函数$H(x)$(储存函数)使得：
$$u^{T}y\le \dot{H}=\frac{\partial H}{\partial x}f(x,u)=L_{f}H(x)$$
则系统是无源的

4.0.4 耗散性、无源性与稳定性

系统：
$$S:\{\begin{array}{l}\dot{x}=f(x,u),\\ y=h(x)\end{array}$$
为耗散无源系统，且$H(x)\ge 0$为相应的存储函数。$H(x)$在$x=0$处取严格最小值，即$H(x)>H(0),\forall x\ne 0$,则x=0为系统自由运动的 $\dot{x}=f(x,0)$的稳定平衡状态。

4.1 遥操作系统的绝对稳定性

稳定性分析（很多公式和上面是重复的，因为再看稳定性的时候前面已经忘了，翻过来翻过去也很麻烦，又理了一遍）

动力学：

$m_m{\ddot{x}}_m(t)+b_m{\dot{x}}_m(t)=u_m(t)+f_h(t)$

$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_s(t)+f_e(t)$

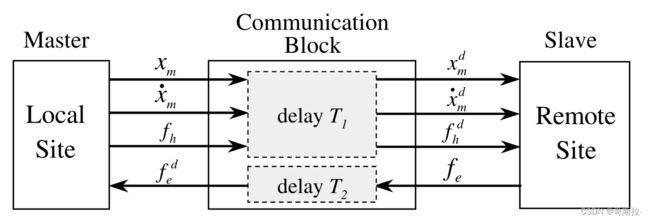
信息延迟表示：

$x_m^d(t)=x_m(t-T_1)，{\dot{x}}_m^d(t)={\dot{x}}_m(t-T_1)$

$f_h^d(t)=f_h(t-T_1)，{\dot{f}}_e^d(t)={\dot{f}}_e(t-T_2)$

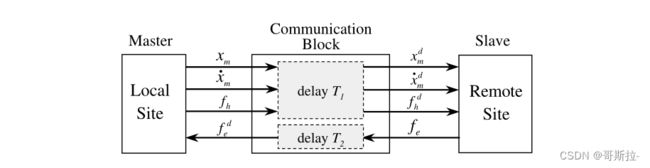
遥操作缩放：
$x_s=k_p{x}_m^d，f_h=k_f{f}_e^d$

主机的阻抗控制器设计：
主机器人理想的阻抗特性：

${\bar{m}}_m{\ddot{x}}_m(t)+{\bar{b}}_m{\dot{x}}_m(t)+{\bar{k}}_m{x}_m(t)=f_h(t)-k_f{f}_e^d(t)$
动力学
$m_m{\ddot{x}}_m(t)+b_m{\dot{x}}_m(t)=u_m(t)+f_h(t)$

消去${\ddot{x}}_m得$

$m_m{\ddot{x}}_m(t)=u_m(t)+f_h(t)-b_m{\dot{x}}_m(t)$

$u_m(t)=(b_m-\frac{m_m}{{\bar{m}}_m}{\bar{b}}_m){\dot{x}}_m(t)+(\frac{m_m}{{\bar{m}}_m}-1)f_h(t)-\frac{m_m}{{\bar{m}}_m}(k_f{f}_e^d(t)+{\bar{k}}_m{x}_m(t))$

从机基于阻抗控制的滑模控制器设计：

${\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)=-f_e(t)$

$\tilde{x}=x_s(t)-k_p{x}_m^d(t)$

动力学

$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_s(t)-f_e(t)$

阻抗误差：

$I_e={\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t)$

只有当 $I_e$ 等于0才能获得所需的阻抗特性，根据误差定义滑模面：

$s=\frac{1}{{\bar{m}}_s}{\int }_0^t{I}_e(\tau )d\tau =\dot{\tilde{x}}(t)+\frac{{\bar{b}}_s}{{\bar{m}}_s}\tilde{x}(t)+\frac{1}{{\bar{m}}_s}{\int }_0^t[{\bar{k}}_s\tilde{x}(\tau )+f_e(\tau )]d\tau$

$\dot{s}=\ddot{\tilde{x}}(t)+\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)]$

由$\dot{s}=0$与动力学联立得

$$\begin{array}{rl}{u}_{eq}& ={\hat{m}}_s(-(\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)]))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)\\ & =\frac{{\hat{m}}_s}{{\bar{m}}_s}({\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)\end{array}$$
但实际上我们需要加一项使得 $s$ 收敛到 0,并且带入主机器人动力学方程消去二阶项

$u_{s2}(t)=u_{eq}(t)-K_{g}sat(\frac{s(t)}{\Phi })$

$u_{s2}(t)=\frac{{\hat{m}}_s}{{\bar{m}}_s}({\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)$

${\bar{m}}_m{\ddot{x}}_m^d(t)+{\bar{b}}_m{\dot{x}}_m^d(t)+{\bar{k}}_m{x}_m^d(t)=f_h^d(t)-k_f{f}_e^{dd}(t)$

${\ddot{x}}_m^d(t)=\frac{1}{{\bar{m}}_m}(f_h^d(t)-k_f{f}_e^{dd}(t)-({\bar{b}}_m{\dot{x}}_m^d(t)+{\bar{k}}_m{x}_m^d(t)))$

$u_{s2}(t)=\frac{{\hat{m}}_s}{{\bar{m}}_s}({\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+\frac{{\hat{m}}_s{k}_p}{{\bar{m}}_m}(f_h^d(t)-k_f{f}_e^{dd}(t)-({\bar{b}}_m{\dot{x}}_m^d(t)+{\bar{k}}_m{x}_m^d(t)))-K_{g}sat(\frac{s(t)}{\Phi })$

总结一下，

$u_{s2}(t)=\frac{{\hat{m}}_s}{{\bar{m}}_s}({\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t))+{\hat{b}}_s{\dot{x}}_s(t)+f_e(t)+{\hat{m}}_s{k}_p{\ddot{x}}_m^d(t)-K_{g}sat(\frac{s(t)}{\Phi })$

$m_s{\ddot{x}}_s(t)+b_s{\dot{x}}_s(t)=u_{s2}(t)-f_e(t)$

$\dot{s}=\ddot{\tilde{x}}(t)+\frac{{\bar{b}}_s}{{\bar{m}}_s}\dot{\tilde{x}}(t)+\frac{1}{{\bar{m}}_s}[{\bar{k}}_s\tilde{x}(t)+f_e(t)]$

$\tilde{x}=x_s(t)-k_p{x}_m^d(t)$

总结为这个形式，便于确定 $K_g$ 的范围，使得 $s=0$

$m_s\dot{s}(t)=-(\alpha (t)+K_{g}sat(\frac{s(t)}{\Phi }))$

其中：

得出

$K_g\ge m_s(\eta +|\alpha (t)|)$

对于双向控制系统，我们将其等效为一个二端口网络模型，绝对稳定性用于分析二端口遥操作的稳定性
Definition of absolute stability：A linear two-port is said to be absolutely stable if there exists no set of passive terminating one-port impedances for which the system is unstable. If the net-work is not absolutely stable, it is potentially unstable.
A necessary and sufficient condition for the absolute stability of a two-port net-
work is that one-port networks, resulting from any passive output and input termi-
nation, are themselves passive.Llewellyn’s stability criteria provides the necessary and sufficient conditions for the absolute stability:

用二端口网络模型来描述我们的双向控制系统，以分析稳定性：

$\left[\begin{array}{c}{F}_h(s)\\ -V(s)\end{array}\right]=\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\end{array}\right]\left[\begin{array}{c}{V}_m(s)\\ -F_e(s)\end{array}\right]$

根据式：

和式：

${\bar{m}}_m{\ddot{x}}_m(t)+{\bar{b}}_m{\dot{x}}_m(t)+{\bar{k}}_m{x}_m(t)=f_h(t)-k_f{f}_e^d(t)$

${\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)=-f_e(t)$

$\tilde{x}=x_s(t)-k_p{x}_m^d(t)$

$I_e={\bar{m}}_s\ddot{\tilde{x}}(t)+{\bar{b}}_s\dot{\tilde{x}}(t)+{\bar{k}}_s\tilde{x}(t)+f_e(t)=0$

计算二端口h的值（这里：e的出现涉及到拉普拉斯变换得位移定理）

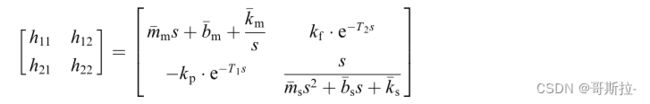
我们只要合理设计参数，使得 h 满足 Llewellyn 稳定性准则，双向控制系统即是稳定的。