李宏毅机器学习笔记（2016年的课程）：Support Vector Machine (SVM)
1. 各种loss函数
f = np.arange(-3, 3 + 1e-8, 0.001)
py = np.array([1.] * len(f))
def get_ideal(yf):
return np.where(yf>=0, 0, 1)
def square(yf):
return np.square(yf - 1.)
def sigmoid(x):
return 1. / (1 + np.exp(-x))
def square_sigmoid(yf):
return np.square(sigmoid(yf) - 1.)
def cross_entropy(yf):
return np.log(1 + np.exp(-yf))
def hinge_loss(yf):
return np.where(1 - yf > 0, 1 - yf, 0)
plt.plot([0] * len(f), np.linspace(-0.2, 3.2, len(f)), color='black', linewidth=0.75)
plt.plot(py*f, get_ideal(py*f), label='ideal', color='black')
plt.plot(py * f, square(py*f), label='square', color='red')
plt.plot(py * f, square_sigmoid(py*f), label='square_sigmoid', color='blue')
plt.plot(py * f, cross_entropy(py * f) / np.log(2), label='cross_entropy', color='green')
plt.plot(py * f, hinge_loss(py * f), label='hinge_loss', color='purple')这一课是讲SVM的，所以正例 
，负例 
，用 
表示模型的输出。纵轴表示损失函数，横轴表示 
，绘图如下：
若是分开两种标签对模型输出绘图， 和上图一样， 如下图所示：
a.黑色的线表示理想状态的损失函数，当模型输出大于0的时候最终输出1，小于0的时候最终输出-1，统计最终输出和标签不同的样本的数目，单个样本表示见上图 黑色 的 “ideal” 图例
但是这个函数无法用梯度下降求解，梯度见下图，在所有可微的点其梯度均为0。我们无法直接优化它，所以用 
来近似 
函数，这个 loss function 长啥样就随我们自己定义了。总体来说，我们期待正例的时候 越正越好，负例的时候 越负越好，换种表示的话也可以理解为 
越正越好。理想状况，相乘是负数得到的 loss 就是1，反之相乘同号的话 loss 就是0。
b.平方损失，我们期待，正例的时候模型输出越接近1越好，负例的时候模型输出越接近-1越好。换言之， 越接近1越好。见上图 红色 的图例 “square” 。公式表示如下：
但是，这个函数是不合理的，我们不希望 乘起来很大的时候会有很大的 loss 。
c.sigmoid + square loss ，我们期待，正例的时候 
接近1，负例的时候 接近0。见上图 蓝色 的图例 “square_sigmoid” 。公式表示如下：
但是我们如果使用了 sigmoid 函数，通常不会使用平方损失做损失函数。因为这样不好训练，具体的见梯度图，例如当时正例的时候，模型的输出在很大的负数的地方梯度也很小，也就是说在很大的负数（并不是我们真正想要的结果）的地方参数更新的会很慢，对于很 负 的值模型没有很大的动力去调整，因为调整了之后对 loss 的影响也不是很大，这一点可以与 cross entropy 对应起来看， cross entropy 在负的很大的地方调整会对 loss 有比较大的影响，所以模型会有动力去调整，这一点也可以参见 cross entropy 的梯度图。
c.cross entropy，我们在使用了 sigmoid 函数之后，通常会使用 cross_entropy 做损失函数。见上图 绿色 的图例 “cross_entropy” ，这边除以了 
，可以让它变成 ideal loss 的 upper bound 。公式表示如下：
d.hinge loss ，与 cross entropy 不同的是，我们不会在输出前接 sigmoid 函数，而是直接套 hinge loss，正例的时候只要模型输出大于1损失函数就是0，负例的时候只要模型输出小于-1的时候损失函数就是0，换句话说，只要 大于1的时候就是完美的了，再大也没有帮助，反映在梯度上就是大于1的梯度均为0，参数不再更新；在0-1之间，它们是同向的，machine 在做分类的时候已经可以得到正确答案，但是 hinge loss 会认为还不够好，他认为要比正确的答案好过一段距离（margin），体现在梯度上就是梯度不为0，还能够通过梯度下降来更新参数使得损失函数继续减小，至于 margin 为啥是1，一个解释是只有1才是 ideal loss 的 tight 的 upper bound 。见上图 紫色 的图例 “hinge_loss”。公式表示如下：
cross entropy VS hinge loss
- 不同点在于对待那些已经能很好的分类的样本，如上图，我们将 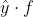从1挪到2，cross entropy 可以使 loss 下降，所以 cross entropy 会想要好的还要更好，但是 hinge loss 是一个及格就好的损失函数，只要大过 margin 就结束了。
- 相对而言，hinge loss 不是很害怕 outlier ，比较robust
梯度如下图所示：
