高效深度学习软硬件设计——神经网络压缩

目录

问题引出

高效推断的算法

Pruning模型剪枝

步骤

剪去参数——形状不规则

剪去神经元——形状仍然规则

Why Pruning

Pruning Changes Weight Distribution

Weight clustering  聚类权重

霍夫曼编码

Quantization量化理论

Low Rank Approximation低秩近似

全连接层

Depthwise Separable Convolution

Binary / Ternary Net 二元/三元网络

Winograd Transformation  Winogradz转换

高效训练的算法

Parallelization

数据并行

模型并行

超参数并行

多机训练 

Mixed Precision with FP16 and FP32

Model Distillation模型精馏

原理

原因分析：Teacher Network会提供額外的信息

Temperature for softmax

DSD: Dense-Sparse-Dense Training

Dynamic Computation 

动态调整网络深度（Dynamic Depth）

动态调整网络宽度（Dynamic Width）

让network自行决定宽度和深度

高效推断的硬件

GPU

Google TPU

Roofline Model

EIE(Efficient Inference Engine)

高效训练硬件

展望

---

问题引出

我们有将模型部署在资源受限的设备上的需求，比如很多移动设备，在这些设备上有受限的存储空间和受限的计算能力。由此带来深度学习面临的挑战：模型大小越来越大，难以在移动设备更新；所需要的训练时间越来越长（即使在大型设备上）；能耗越来越大（模型越大，需要的访存操作也越多，能耗大头）。因此要压缩空间大小、加快计算速度等。

解决办法：算法和硬件的协同设计Improve the Efficiency of Deep Learning by Algorithm-Hardware Co-Design

高效推断的算法

Pruning模型剪枝

神经网络的参数有很多，但其中有些参数对最终的输出结果贡献并不大，相反就显得冗余，将这些冗余的参数剪掉的技术称为剪枝。

剪枝可以从权重入手，也可以从神经元入手。剪枝可以减小模型大小、提升运行速度，还可以防止过拟合，同时保持准确度基本不变。还可以减少访存，节能。

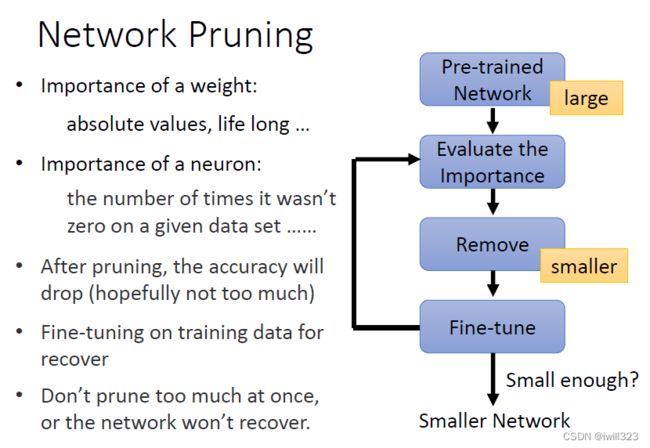
步骤

1. 训练一个大的模型

2. 评估权重或神经元的重要性

   1. 每个参数的重要性
      • 看绝对值大小
      • 套用Life-long learning的思想，计算bi 的值
   2. 每个神经元的重要性
      • 计算神经元输出不为0的次数

3. （对权重或者神经元的重要性进行排序），移除不重要的参数或神经元，减小模型大小。经过剪枝，模型性能会下降

4. 使用原来的训练数据微调剩余的参数

5. 循环进行

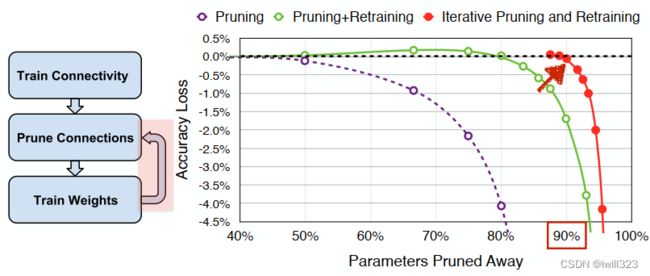
为了不会使剪枝造成模型效果的过大损伤，每次不会一次性剪掉太多的权重或神经元，因此这个过程需要迭代，也就是说剪枝且微调一次后，如果剪枝后的模型大小还不令人满意，就迭代上述过程直到满意为止。

下图一直剪掉了90%的权重

 下面把模型剪了95%就不行了

 

剪去参数——形状不规则

剪枝权重的问题是会造成网络结构的不规则（每个节点的输出和输出节点数都会变得不规则），在实际操作中很难去实现，也很难用GPU去加速矩阵运算。实际上是使用0来代替被剪掉的权重，模型实际上没有变小

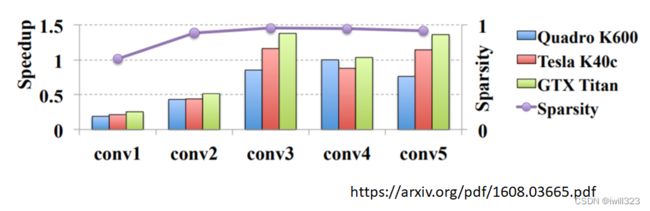
实验结果表明，即使剪掉95%的参数，但是运算时大多数时候加速比小于1，并没有变得更快。

剪去神经元——形状仍然规则

删减neuron之后网络结构能够保持一定的规则，实现起来方便，而且也能起到一定的加速作用。

通过上述可知，实际上做weight pruning是很麻烦的，通常我们都进行neuron pruning，可以更好地进行implement，也很容易进行speedup。 

Why Pruning

先要训练一个大的Network，然后再去把它变小，得到的小 Network 跟大 Network正確率沒有差太多，为什么不直接训练一个小的Network呢？因为一个大的Network比较容易训练。

解释：大乐透假说

大的 Network可以視為是很多小的 Sub-network 的組合。當我們去訓練這個大的 Network 的時候，等於是在訓練很多小的 Network。

一個小的 Network不一定可以成功的被訓練出來，不一定可以通过 Gradient Descent找到一個好的 Solution讓它的 Loss 變低。但是对于大量的 Sub-network，只要其中一個成功，大的 Network 就成功了。 那么大的 Network 裡面，如果包含的小的 Network 越多，就好像是去買樂透的時候，買比較多的彩券一樣，彩券越多，中獎的機率就越高。所以一個 Network 越大，它就越有可能成功的被訓練起來。

Pruning Changes Weight Distribution

 

Weight clustering  聚类权重

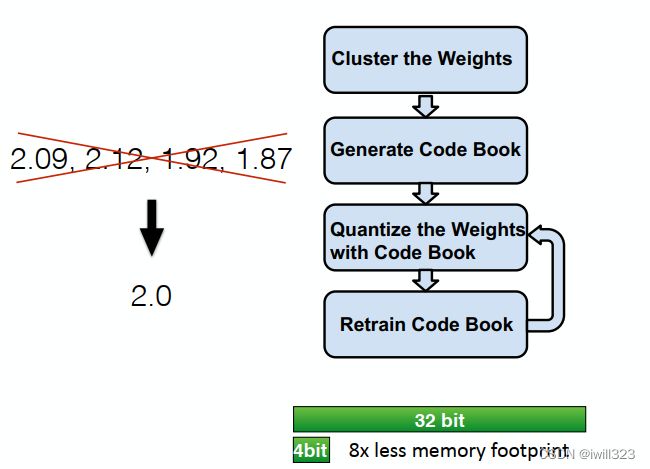
若干个比较接近的权重分为一类，用一个数（平均）来代替这一群数据，这样对于一个模型就只需要记录：

• 模型的每一个参数属于哪一个类：如果只有4群，用2bit的数字即可表示。

• 每一群参数使用哪一个数字来代替：用一个表进行记录

于是每个参数用更少的位数存储。结果是会导致误差变大，不过也有可能避免数字太精准可能导致的过拟合。

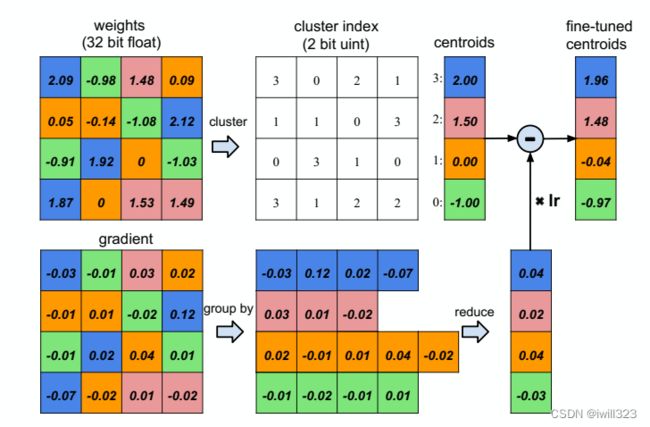
左边表示网络中正常权重矩阵，将相近权值聚为一类，得到一个聚类中心（centroids）向量，权重矩阵存储的是类别号，只需要2个bit，而不是整个32位浮点数，存储空间下降 。得到梯度后，将梯度按照权重类别（cluster index）分类，求和得到梯度向量，乘以学习率，再从原始的权重中心减去权值，得到新的权重中心向量，完成一个随机梯度下降迭代

经过处理，权值由左边的连续变成了右边的离散。对权重离散值取对数可以知道只需要多少位的数来标识权重。训练中权重会被调节（adjust），这种微小的调整可以补偿准确率的损失

 需要保留多少位：CNN：到4位以下，准确度才开始下降；FC：2位

Pruning + Trained Quantization Work Together：将这两种方法结合到一起，我们会发现，在不影响准确率的要求下，单个方法可以将模型压缩到10％，而两个方法同时用可以压缩到3％。

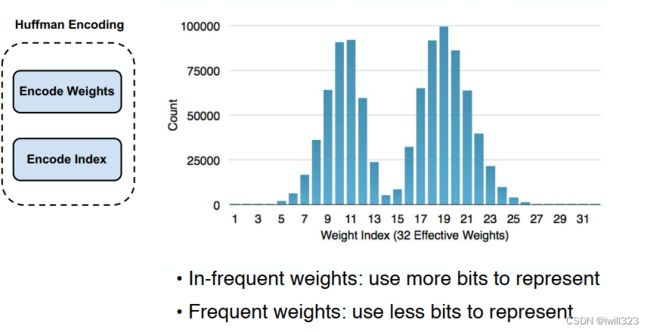
霍夫曼编码

对于每个类别的“类别号”，用较长的编码表示不常出现的权重，用较短的编码表示常出现的权重

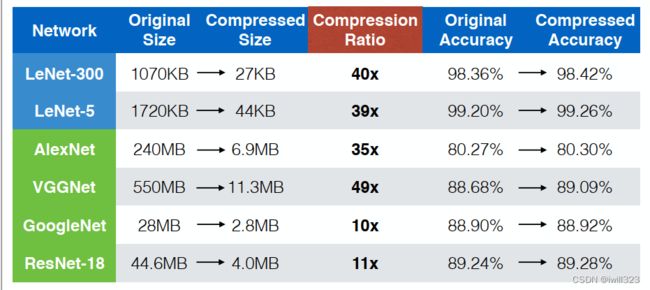
 在不影响准确率的要求下，这三种方法联合使用可以降低10到49倍的模型复杂度。

 

 即使对于小模型也很有效

 

1

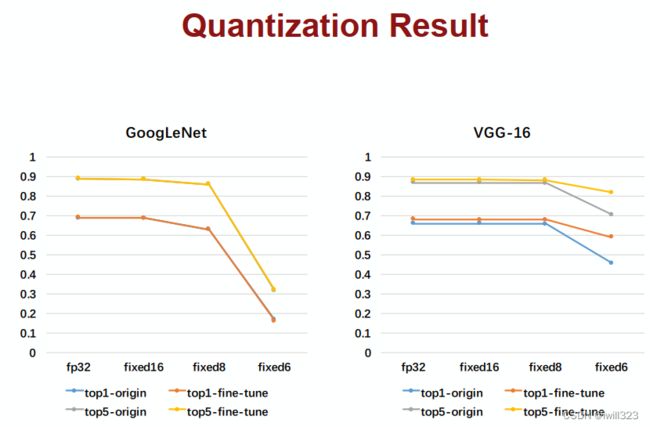
Quantization量化理论

广泛应用于TPU设计（TPU只使用8位来推断）。这一部分没有看懂。。。

步骤：

• Train with float  用标准浮点数训练网络
• Quantizing the weight and activation:
    • Gather the statistics for weight and activation  如最大值、最小值、需要多少位数来表示该范围
    • Choose proper radix point position  用这些位数表示整数，剩下的位数表示其他部分
• Fine-tune in float format
• Convert to fixed-point format 用定点数前向传播，用浮点数反向传播并更新权值

 使用8位数，模型准确率下降不大

Qiu et al. Going Deeper with Embedded FPGA Platform for Convolutional Neural Network, FPGA’16

Low Rank Approximation低秩近似

全连接层

左边是一个普通的全连接层，输入有 N 个 Neuron，输出有 M 个 Neuron，两层之间的参数量W就是 N x M ，只要 N 跟 M 其中一者很大，这个 W 的参数量就会很大。

为了减少参数量，可以在 N 跟 M 中间再插一层，这一层 Neuron 的数目是 K。

原来一层的 Network，参数量是 M x N；现在拆成两层 Network，第一层U的参数量是 N x K，第二层V是 K x M。如果你 K 远小于 M 跟 N，那U 跟 V 的参数量加起来，比 W 还要少的多，所以插入一层后参数减少了。

限制：低秩近似之所以叫低秩，是因为原来的矩阵的秩最大可能是min(M,N)，而新增一层后可以看到矩阵U和V的秩都是小于等于K 的，矩阵秩运算公式rank(AB)≤min(rank(A),rank(B))，所以相乘之后的矩阵的秩一定是小于等于K 。
那么这样会带来什么影响呢？那就是原先全连接层能表示更大的空间，而现在只能表示小一些的空间，会限制原来的NN能做的事情。

Depthwise Separable Convolution

1. Depthwise Convolution——考虑一个channel内部的关系

• filter数目和channel数目一样
• 每个filter负责一个channel，分别对一个feature map进行卷积
• input channel 和 output channel 数目也一样
• channel 之间没有“互动”

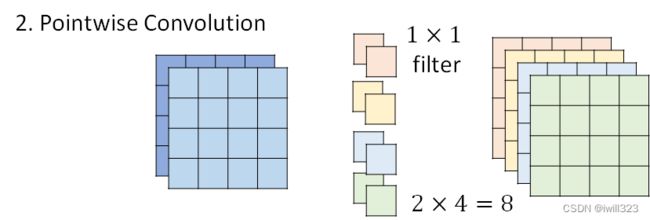
2. Pointwise Convolution——考虑channel之间的关系

在Depthwise Convolution的基础上，进一步进行操作。

• filter size 限制为 1，通道数量等于输入数据的通道数量
• 按照正常的CNN做法做卷积
• 输入channel和输出channel的数目可以不同

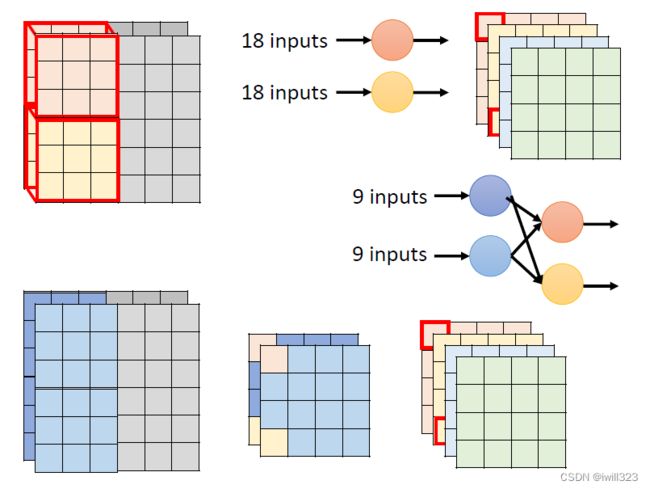
二者关系

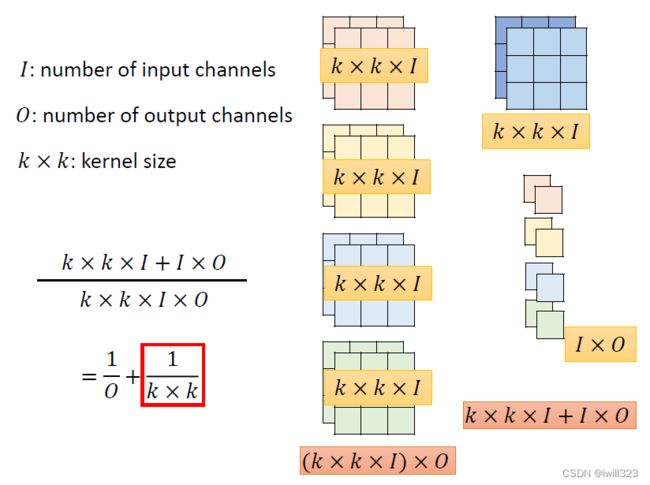
考察右侧左上角红色框内数据的来源，都是来自左侧原图中左上3×3×2的区域，只是在Depthwise Separable Convolution中，将原来的“一次卷积”的操作改为“两次卷积”，以此减少参数量。

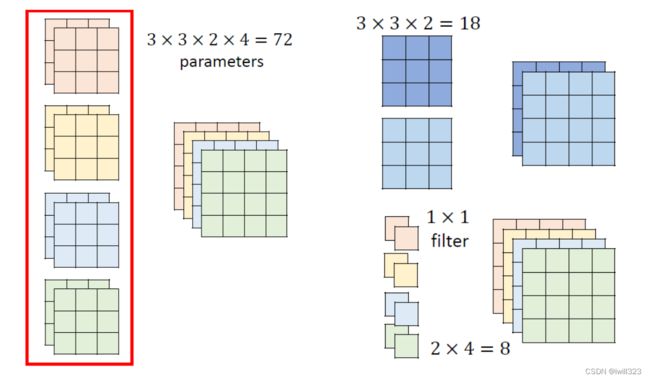
参数量变化

实际例子。

左侧为一般的卷积需要的参数量；右边是Depthwise Separable Convolution需要的参数量。

计算可得，两者的参数量之比主要取决于1/(k×k)。

Binary / Ternary Net 二元/三元网络

用二元或三元权重来表示整个网络。比如每个权重只用1或-1来表示。

可以看到把权重限制为+1或者-1相当于加上了正则化，但还是比不过Dropout方式

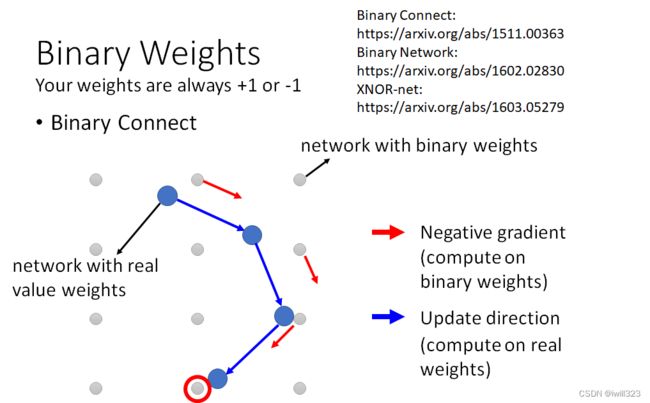
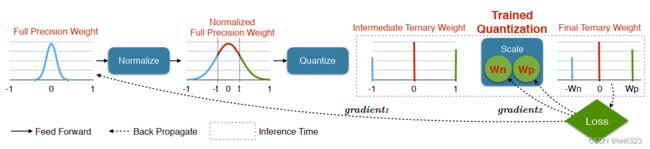
训练时保存完全精确权重，推断时仅保留尺度因子和三元权值。如下图示，灰色节点表示使用binary weight的神经元，蓝色节点可以是随机初始化的参数，也可以是真实的权重参数。

第一步，先计算出和蓝色节点最接近的二元节点，并计算出其梯度方向（红色剪头）。

第二步，蓝色节点按照红色箭头方向更新，而不是按照他自身的梯度方向更新。梯度下降后，蓝色节点到了一个新的位置。

最后在满足一定条件后(例如训练之最大epoch)，蓝色节点会停在一个灰色节点附近，用该灰色节点的权重。

效率更高，模型更小。

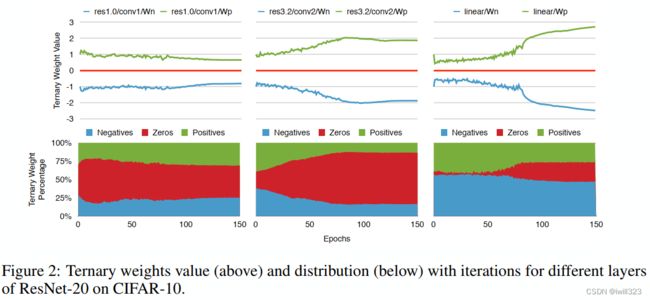
 下面是三元权值的绝对值，以及比重在训练过程中的变化

 卷积核可视化

 AlexNet Error Rate on ImageNet

Winograd Transformation  Winogradz转换

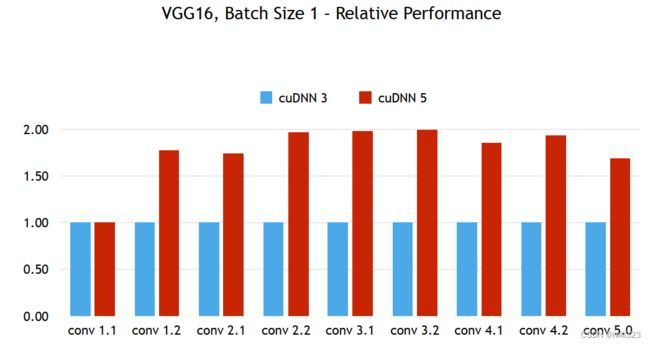
 对于3*3卷积，如果输入矩阵是4*4，那么要做36次乘加操作；使用了Winogradz转换，将卷积核变成4*4，同时也变换输入数据，这样只需要16次乘加操作。 cudnn5之后，计算卷积就使用了该方法

 

详解Winograd变换矩阵生成原理 - 知乎

高效训练的算法

Parallelization

数据并行

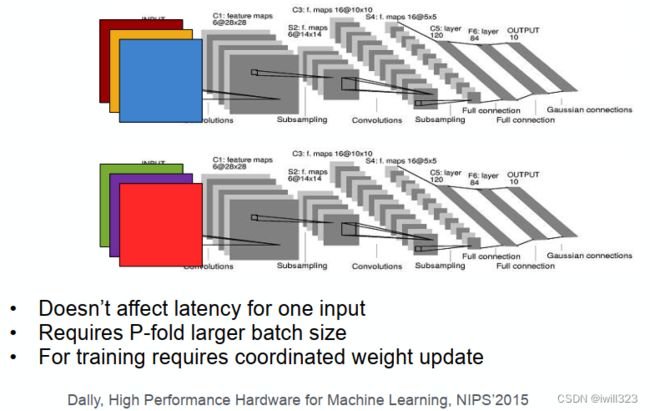
跨多个GPU对一个批次的数据进行拆分，同时处理。不是让单个处理时间变短，而是让每个批次处理数量更多。如果有四台机器，则每次批处理的数据量就能达到原来的4倍

在完成每个小批量数据的训练之后，梯度在GPU上聚合，即同步只需要在每个小批量数据处理之后进行。有一个参数服务器作为主服务器，3个从属服务器各自训练一部分数据，将计算出来的梯度传到主服务器，返回得到更新后的参数。当其他梯度参数仍在计算时，完成计算的梯度参数就可以开始交换。

除了选择GPU 0进行聚合，然也可以选择CPU上聚合，事实上只要优化算法支持，在实际操作中甚至可以在某个GPU上聚合其中一些参数，而在另一个GPU上聚合另一些参数。例如，如果有四个与参数向量相关的梯度1,…,4，还可以一个GPU对一个(=1,…,4）地进行梯度聚合。

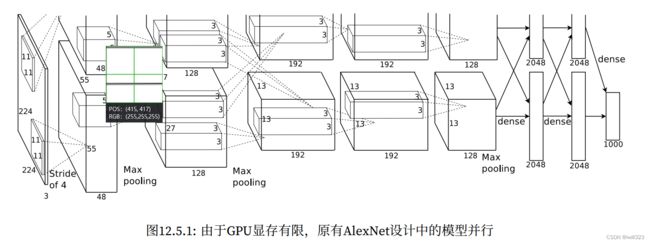
模型并行

将模型切割，分给不同的线程或处理器处理。比如下图将一个图片分成4份，每个线程或处理器解决一份。块与块衔接的地方需要额外注意

也可以拆分输入或输出特征映射feature map（也就是通道）实现并行。

 对于全连接的层，同样可以拆分输出单元的数量，用两个线程并行处理

需要大量的同步或屏障操作（barrier operation），因为每一层都依赖于所有其他层的结果。 此外，需要传输的数据量也可能较大。 因此，基于带宽的成本和复杂性，不推荐这种方法。 

超参数并行

在不同的机器上调整学习效率和权值衰减，以达到粗略的并行Hyper-Parameter Parallel
 在不同的计算上调试学习率、权重衰减等参数

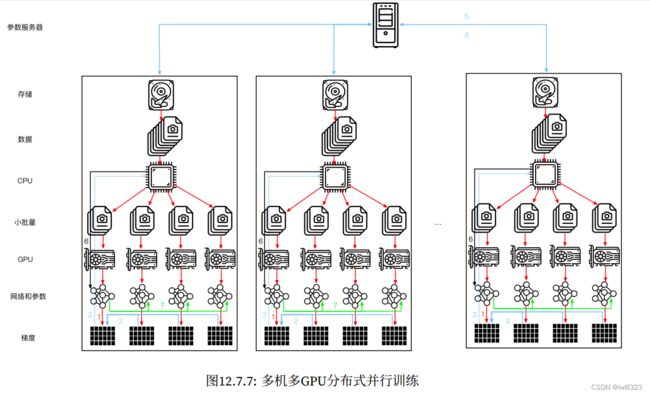
多机训练 

在多台机器上进行分布式训练，需要服务器之间相互通信，而这些服务器又只通过相对较低的带宽结构连接，在某些情况下这种连接的速度可能会慢一个数量级，而且在不同机器上运行训练代码的速度会有细微的差别，因此跨设备同步是个棘手的问题。

分布式并行训练：

1. 在每台机器上读取一组（不同的）批量数据，每台机器在多个GPU之间分割数据并传输到GPU的显存中。基于每个GPU上的批量数据分别计算预测和梯度。
2. 来自一台机器上的所有GPU的梯度聚合在一个GPU上（或者在不同的GPU上聚合梯度的某些部分）。
3. 每台机器的梯度被发送到本地CPU中。
4. 所有的CPU将梯度发送到中央参数服务器中，由该服务器聚合所有梯度。
5. 使用聚合后的梯度来更新参数，并将更新后的参数广播回各个CPU中。
6. 更新后的参数信息发送到本地一个（或多个）GPU中。
7. 所有GPU上的参数更新完成。

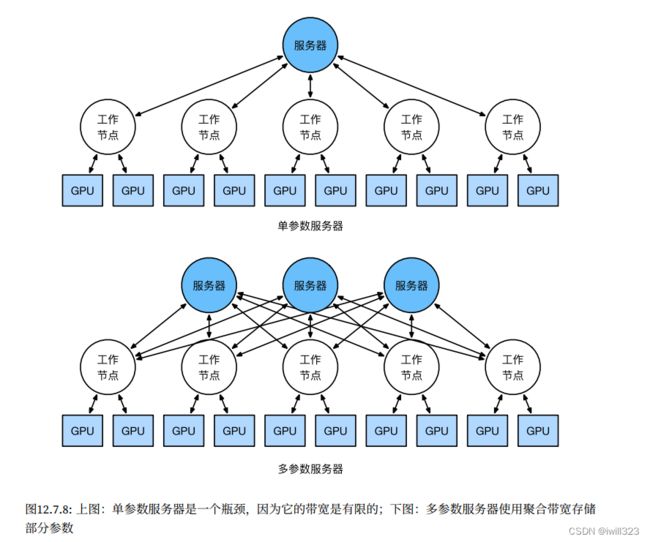
当我们考虑多台机器时，会发现中央的参数服务器成为了瓶颈。毕竟，每个服务器的带宽是有限的，因此对于个工作节点来说，将所有梯度发送到服务器所需的时间是O(m)。我们也可以通过将参数服务器数量增加到来突破这一障碍。此时，每个服务器只需要存储O(1/n)个参数，因此更新和优化的总时间变为O(m/n)。在实际应用中，我们使用同一台机器既作为工作节点还作为服务器。设计说明请参考下图。特别是，确保多台机器只在没有不合理延迟的情况下工作是相当困难的。

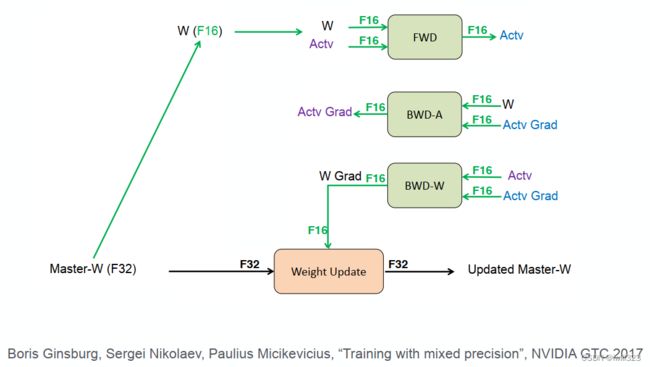
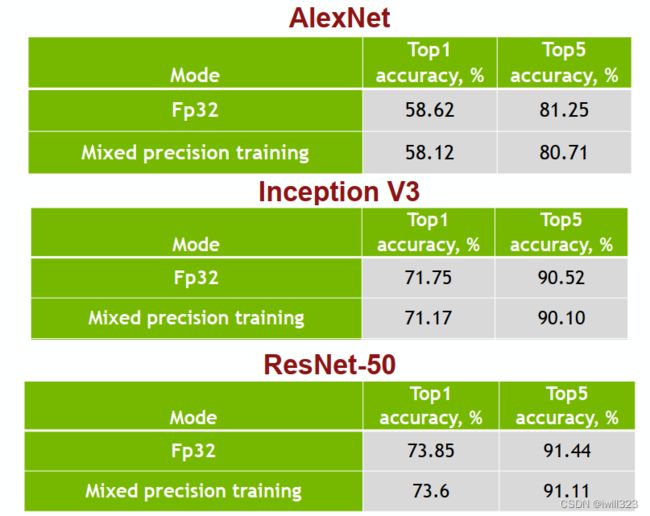
Mixed Precision with FP16 and FP32

FP16和FP32的混合精度训练

能耗和占位面积比较：16位的硬件比32位硬件能耗上效率更高。

16位作乘法，32位作加法，用32位存储

 得到16位梯度，更新权值的时候用32位

 

 

Model Distillation模型精馏

原理

让小网络去学习大网络的运作。训练一个大网络Teacher Network，将这个大网络的输入与输出作为小网络Student Net的训练集数据，并不是让小网络直接学有标签的原始训练集数据。

训练时，使小网络的输入与大网络的输入相同，计算两者输出的cross-entropy，使其最小化，从而可以使两者的输出分布相近。就算老師的答案是錯的，也让學生去學錯的東西。

Teacher Network（老师）也可以是多个模型的ensemble，再用某种策略将它们结合起来，比如各个模型结果投票或取平均。当ensemble的模型数量很大时，单次计算就需要大量的时间，在实际系统中难以实用，使用知识蒸馏的方式来使得Student Network学习集成模型的输出，从而达到将集成模型的效果复制到一个模型上的目的，这是知识蒸馏的另一个用处。

• 根据Hinton et al. Dark knowledge / Distilling the Knowledge in a Neural Network: Start with a trained model that classifies 58.9% of the test frames correctly. The new model converges to 57.0% correct even when it is only trained on 3% of the data

                   

原因分析：Teacher Network会提供額外的信息

Teacher Network的输出提供了比独热编码标签更多的信息。比如看到图片“1”，如果采用one-hot编码，student network难以学会。 1 跟 7、 9 長得有點像，如果要求看到1要輸出 1， 看到7 、9 分數都要是 0，可能很難學起來。 而老师则会告诉他，看到 1 输出是 0.7，看到 7 输出是 0.2，看到 9 输出是 0.1，说明1和7、9长得很像，所以，student跟着teacher net学习，可以得到比label data更多的information。

使用软标签而不是硬标签的另一个好处是，不同的模型给出的预测结果可能是不一样的，使用软标签综合各模型结果，依旧能够得到正确结果。

Student Network有可能辨识从来没有见过的输入，比如把Student Network的训练资料中的数字7移除后，可能训练完成后也会认识数字7，这是因为Teacher Network输出的soft label提供了额外的信息。

Temperature for softmax

Softmax可以让数值变成概率分布，数值大小处于0-1之间。在进行softmax之前，将数值除以一个超参数T，使得softmax的结果变得更加平滑，小网络能准确地学到大网络的输出

• 如果老师的结果非常集中，不够平滑，实际上退化成直接看label的one-hot编码，老师提供的额外信息没法得到很好地利用
• 利用Temperature的技术，可以保留类别之间的“微弱”关系，更好地利用老师提供的额外信息。
• 过大的Temperature会让所有的数值都趋于0，得到的分布退化成“均匀分布”，同样没有意义。

 

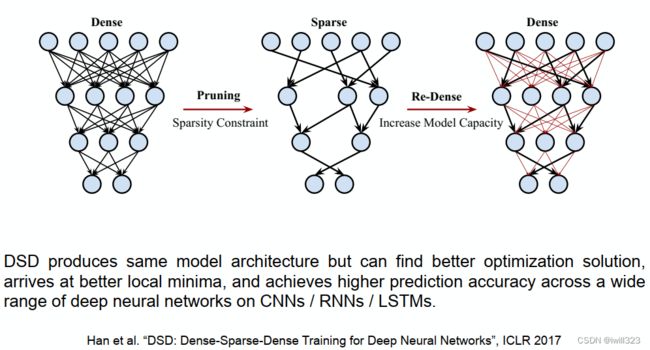
DSD: Dense-Sparse-Dense Training

在做了剪枝等简化处理后，再次添加神经元间的连线并训练。实验表明这能提升1％到4％的精确度

 

Dynamic Computation 

希望network可以根据实际运算资源的情况，自动调整其需要的运算量。该方法的主要思路是如果目前的资源充足（比如你的手机电量充足），那么算法就尽量做到最好，比如训练更久，或者训练更多模型等；反之，如果当前资源不够（如电量只剩10%），那么就先算出一个过得去的结果。

如果训练多个模型，那么要占据大量空间，不可行

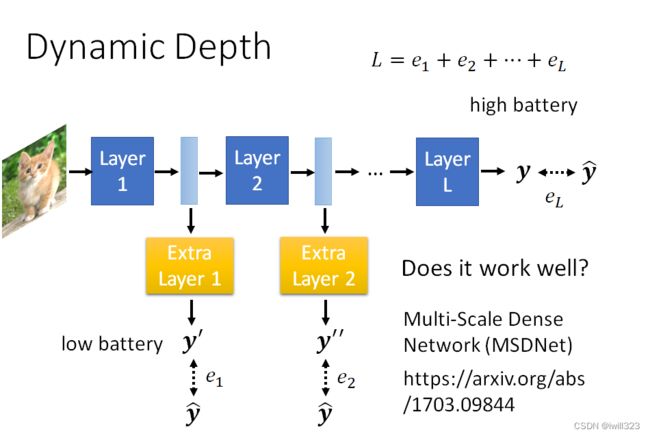
动态调整网络深度（Dynamic Depth）

以目标检测为例，训练一个很深的 Network，在 Layer 和 Layer 中间再加上一个额外的 Layer，这个额外的 Layer 它的工作，是根据每一个 Hidden Layer 的 Output，去决定现在分类的结果应该是什么。

• 当运算资源比较充足的时候，可以让这张图片去跑过所有的 Layer，得到最终的分类结果；
• 当运算资源不充足的时候，可以让 Network 决定要在哪一个 Layer 自行做输出；

如何训练：我们希望让 Ground Truth 跟每一个 Extra Layer 的 Output 越接近越好，所以就把所有的 Output跟 Ground Truth 的 Cross Entropy通通加起来得到 L，再去Minimize L。

其他方法：MSDNet

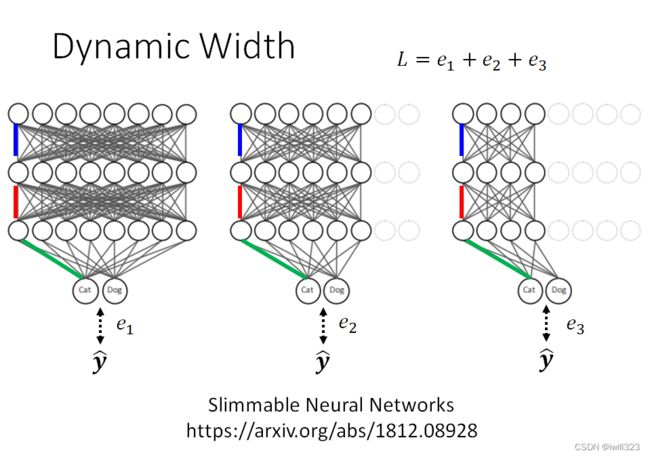
动态调整网络宽度（Dynamic Width）

所谓的“不同宽度”，指的是同一个网络中使用到的参数量不同。图中一样颜色的是同一个参数

对同一个network设定好几个不同的宽度，在训练的时候同一张图片丢进去，每个不同宽度的 Network 会有不同的输出，每一个输出都跟正确答案越接近越好。

把所有的输出跟 Ground Truth 的距离加起来得到一个 Loss，然后 Minimize 这个 Loss 。

让network自行决定宽度和深度

根据输入数据的“难易程度”，让network自行决定执行的宽度和深度。 比如遇到一个简单的问题，一层Layer就会结束；遇到一个复杂的问题，需要很多层Layer才会结束

高效推断的硬件

目标：较少访存，从而降低能耗

GPU

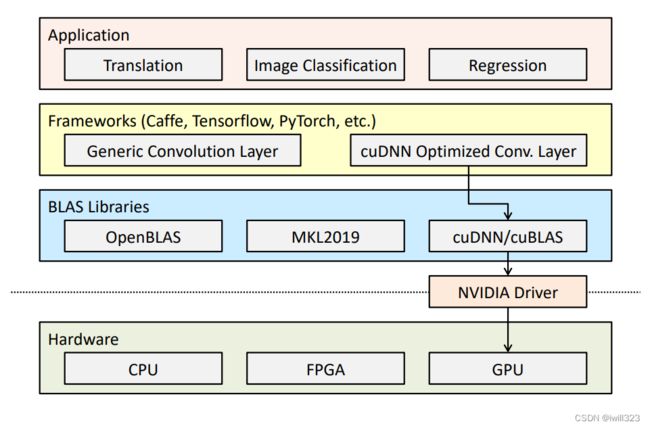
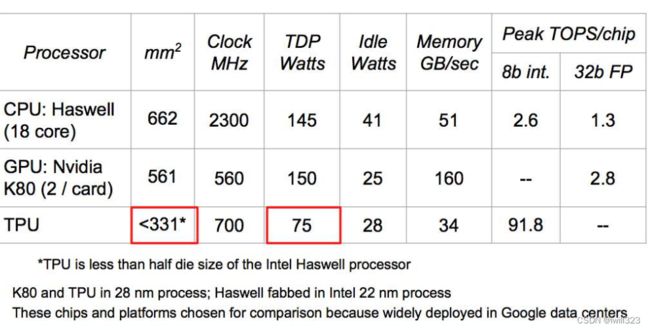
Google TPU

性能怪兽

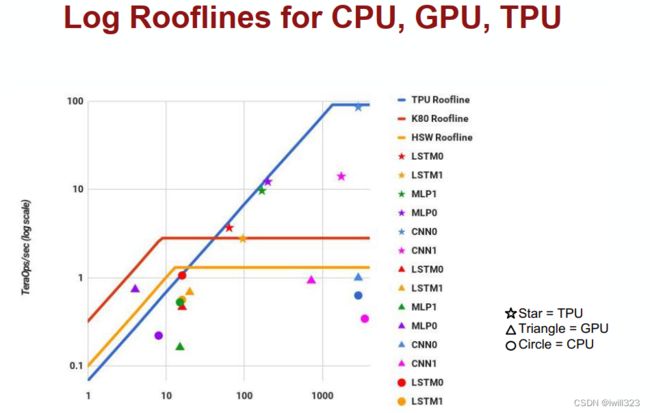
Roofline Model

横坐标是数学运算强度（硬件在数学运算和在访存上开销的比例），纵坐标是硬件实际性能。如果访存多、计算少，那么存储器带宽就是性能瓶颈，硬件性能发挥较差；反之，计算能力是性能瓶颈。

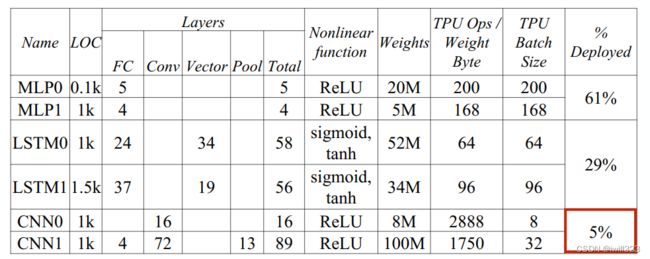
不同模型对硬件性能的发挥。CNN能很好地发挥硬件性能，有些模型（如LSTM）只能发挥不到硬件性能峰值的10%，原因在于他们为了保证用户体验，所以要降低延迟，图像和语音这样的数据不能等待所有的用户数据，而是分成大量的小批次送入模型，于是访存次数高，限制了硬件性能发挥

 下图说明了上述解释

 

EIE(Efficient Inference Engine)

减少访存，降低存取带宽要求 =>  压缩模型 => 建立可以在压缩模型上推断的硬件

简单来说，它的思想是跳过稀疏数据的权重（不存储，不计算）和激活值（忽略为0的激活值），以及使用近似的值来代替精确值（用4位而不是32位）。根据前面的研究，这对精确度几乎没有影响。

下图中第一列10与5的差距源于索引的开销

只存储非0值的权重，节省取数消耗的带宽

 

 提升非常惊人（图略）

高效训练硬件

计算能力、存储带宽和内部通信是决定性能的最重要因素

TPU是Google推出的专门用于加速TensorFlow运算的处理器，其选择了8bit的定点运算。

展望

参考：李宏毅机器学习笔记—— 15. Network Compression( 网络压缩)_HSR CatcousCherishes的博客-CSDN博客