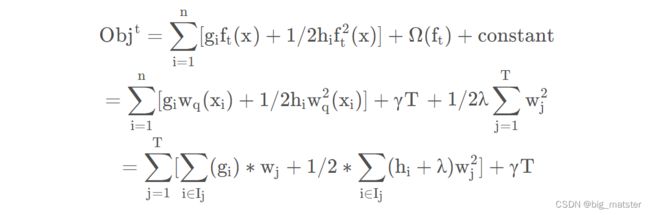文本分类从入门到精通—常用模块的基本用法
Xgboost算法介绍
一、简介
Xgboost有叫做极度提升树,是boosting算法的一种实现方式,针对分类或回归问题,效果非常的好,在各种数据竞赛中大放异彩,而且工业界应用也非常广泛,主要是因为其性能优异,使用简单,速度块等优点,本文从以下方面介绍该算法模型:

二、基本原理
xgb是boostinig算法的一种实现方式,主要是降低偏差,也就是降低模型的误差,因此,其是采用多个基学习器,每个基学习器都比较简单,避免过拟合,下一个学习器就是学习前面基学习器的结果 y i t y^t_i yit和实际值 y i y_i yi的偏差,通过多个学习器的学习,不断降低模型值和实际值的差。
y i 0 = 0 y^0_i = 0 yi0=0
y i 1 = f 1 ( x i ) = y i 0 + f 1 ( x i ) y^1_i = f_1(x_i) = y^0_i + f_1(x_i) yi1=f1(xi)=yi0+f1(xi)
y i 2 = f 1 ( x i ) + f 2 ( x i ) = y i 1 + f 2 ( x i ) y^2_i = f_1(x_i) + f_2(x_i) = y^1_i + f_2(x_i) yi2=f1(xi)+f2(xi)=yi1+f2(xi)
y i t = ∑ k = 1 t f k ( x i ) = y i t − 1 + f t ( x i ) y^t_i = \sum^t_{k = 1}f_k(x_i) = y^{t-1}_i + f_t(x_i) yit=k=1∑tfk(xi)=yit−1+ft(xi)
基本思路就是不断生成新的树,每棵树都是基于上一课树和目标值的差值进行学习,从而降低模型的偏差,最终模型结果输出如下:
y i = ∑ k = 1 t f k ( x i ) y_i = \sum^t_{k = 1}f_k(x_i) yi=∑k=1tfk(xi),即所有树的结果累加起来才是模型对一个样本的预测值,那在每一步如何选择生成一个优秀的模型?那就是由我们的目标函数决定?
目标函数
目标函数由两部分组成,一部分是模型误差,即样本真实值与预测值之间的差值,二是模型的结构误差,即正则项,用于限制模型复杂度。
O b j ( θ ) = L ( θ ) + Ω ( θ ) = L ( y i , y i t ) + ∑ k = 1 t Ω ( f k ( x i ) ) Obj(\theta) = L(\theta) + \Omega(\theta) = L(y_i,y^t_i) + \sum^t_{k = 1} \Omega(f_k(x_i)) Obj(θ)=L(θ)+Ω(θ)=L(yi,yit)+k=1∑tΩ(fk(xi))
因为 y i t = y i t − 1 + f t ( x i ) y^t_i = y^{t - 1}_i + f_t(x_i) yit=yit−1+ft(xi),所以将其带入上面公式转换为:
O b j ( θ ) = L ( θ ) + Ω ( θ ) = L ( y i , y i t − 1 + f t ( x i ) ) + ∑ k = 1 t Ω ( f k ( x i ) ) Obj(\theta) = L(\theta) + \Omega(\theta) = L(y_i,y^{t-1}_i +f_t(x_i)) + \sum^t_{k = 1} \Omega(f_k(x_i)) Obj(θ)=L(θ)+Ω(θ)=L(yi,yit−1+ft(xi))+k=1∑tΩ(fk(xi))
第t棵树的误差由三部分组成:n个样本在第t棵树的误差求和,以及第t棵树的结构误差和前t-1棵树的结构误差。其中,第t-1棵树的结构误差是常数,因为,我们已经知道l第t-1棵树的结构。
假设我们的损失函数是平方损失函数(mse),则上述目标函数转换为:
O b j t = ∑ i = 1 t L ( y i , y i t − 1 + f t ( x i ) ) + Ω ( f t ) + ∑ t = 1 T − 1 Ω ( f t ) = ∑ i = 1 n ( y i − ( y i t − 1 + f t ( x i ) ) ) 2 + Ω ( f t ) + c o n s t a n t Obj^t = \sum^t_{i = 1}L(y_i,y^{t-1}_i + f_t(x_i)) + \Omega(f_t) + \sum^{T-1}_{t=1}\Omega(f_t) \\ =\sum^n_{i=1}(y_i - (y^{t-1}_i+ f_t(x_i)))^2 + \Omega(f_t) + constant Objt=i=1∑tL(yi,yit−1+ft(xi))+Ω(ft)+t=1∑T−1Ω(ft)=i=1∑n(yi−(yit−1+ft(xi)))2+Ω(ft)+constant
上述公式即为损失函数mse对xgb第t步的目标函数,唯一变量即为 f t f_t ft,从此损失函数仍然是一个相对复杂的表达式,所以为咯简化它,采用二阶泰勒近似表达,即:
f ( x + ∇ ( x ) ) = f ( x ) + f ‘ ( x ) ∇ ( x ) + 1 2 f ‘ ‘ ( x ) ∇ ( x 2 ) f(x + \nabla(x)) = f(x) + f^`(x)\nabla(x) + \frac{1}{2}f^{``}(x) \nabla(x^2) f(x+∇(x))=f(x)+f‘(x)∇(x)+21f‘‘(x)∇(x2)

所以当损失函数是mse时, g i = 2 ( y i t − 1 − y i ) g_i = 2(y^{t-1}_i - y_i) gi=2(yit−1−yi) h i = 2 h_i = 2 hi=2
经过转换之后,其中第一项是所有样本与第 t − 1 t-1 t−1棵树误差之和,因为第 t − 1 t-1 t−1棵树是已经知的,所以可以将其视为常数项,我们暂时将其在目标函数中将其舍去,我们的目标函数i变为 f t ( x ) f_t(x) ft(x)函数了,而 f t ( x ) 是关于叶子结点 w 的函数,所以我们将目标函数全部转换为关于 f_t(x)是关于叶子结点w的函数,所以我们将目标函数全部转换为关于 ft(x)是关于叶子结点w的函数,所以我们将目标函数全部转换为关于w$的函数

如此简单,所以在求解目标函数二叉树的时候,只要知道损失函数一阶导数,二阶导数,以及样本落在那个叶子结点上,我们只要求出在每个叶子节点上,该样本的一阶导和二阶导就能求出目标函数。也就能决定是否分裂该节点,依据哪个节点的特征值来进行分裂。
节点分裂
xgb节点是否分裂取决于信息增益的变化,若分裂当前节点,信息增益>0,则进行分裂,若不大于0则不分裂,如何判断分列前后信息增益的变化呢。那就可以使用我们的目标函数来表示了。

贪心算法
贪心算法分裂的方式就是一种暴力搜索的方式,遍历每一个特征,遍历该特征的每一个取值,计算分裂前后的增益,选择增益最大的特征取值作为分裂点。
近似算法
近似算法,其实就是分桶,目的是为了提升计算速度,降低遍历的次数,所以对特征进行分桶。就是将每一个特征的取值按照分位数划分到不同的桶中,利用桶的边界值作为分裂节点的候选集,每次遍历时不再是遍历所有特征取值,而是仅遍历该特征的几个桶(每个桶可以理解为该特征取值的分位数)就可以,这样可以降低遍历特征取值的次数。
分桶算法分为global模式和local模式,global模式就是在第一次划分桶之后,不再更新桶,一直使用划分完成的桶进行后续的分裂。这样做就是计算复杂度降低,但是经过多次划分之后,可能会存在一些桶是空的,即该桶中已经没有了数据。
local模式就是在每次分列前都重新划分桶,优点是每次分桶都能保证各桶中的样本数量都是均匀的,不足的地方就是计算量大。
其它特点
缺失值的处理
对于存在某一维特征缺失的样本,xgb会尝试将其放到左子树计算一次增益,再放到右子树计算一次增益,对比放在左右子树增益的大小决定放在哪个子树。
防止过拟合
xgb提出了两种防止过拟合的方法:第一种称为Shrinkage,即学习率,在每次迭代一棵树的时候对每个叶子结点的权重乘上一个缩减系数,使每棵树的影响不会过大,并且给后面的树留下更大的空间优化。另一个方法称为Column Subsampling,类似于随机森林选区部分特征值进行建树,其中又分为两个方式:方式一按层随机采样,在对同一层结点分裂前,随机选取部分特征值进行遍历,计算信息增益;方式二在建一棵树前随机采样部分特征值,然后这棵树的所有结点分裂都遍历这些特征值,计算信息增益。
总结
睡觉,明天将xgboost视频搜一波然后进行学习与掌握,全部将其搞定都行拉的样子与打算。全部将其搞定都行;啦!