吴恩达教授机器学习课程笔记【六】- Part 6 学习理论
本节为吴恩达教授机器学习课程笔记第六部分,学习理论Learning Theory,主要包括:偏差的方差的含义与理解,联合界引理,霍夫丁不等式(切诺夫界),经验风险最小化,有限集和无限集假设类,VC维。
1. 偏差和方差的权衡
偏差和方差是模型泛化误差的两种的不同衡量标准,讲义里并没有给出两个标准的形式化的定义,而是说,当我们模型非常简单并且参数较少时,可能会有较大的偏差bias但是方差vatiance较小;模型过于复杂且参数较多时,可能会有较大的方差而偏差较小。
比如说如果训练集非常大,且标签和特征并不是线性的惯性,若我们强行使用一个线性模型来拟合数据,得到的模型的泛化误差就会很大,这种情况即欠拟合,我们说模型的偏差很大。如果训练集样本树木有限,但是我们强行使用一个高阶的模型来拟合数据,得到的模型虽然在训练集上表现良好,但是泛化误差同样很大,这情况即过拟合,我们说模型的方差很大。
讲义中给出的描述非常有限,我们在训练一个模型的时候,通常的做法时定义一个损失函数,通过将这个损失最小化,提高模型的性能。但是我们训练模型的目的是解决实际的问题,单纯地将训练数据集的loss最小化,并不能保证在解决更一般问题是模型效果好,甚至不能保证可用。这个训练数据集的loss和一般化的数据集的loss之间的差异,即泛化误差。其中Bias偏差是用所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异,Variance方差是不同训练数据集训练出的模型的输出值之间的差异。
人话就是偏差度量了学习算法的期望预测与真实结果的偏离程度,即算法本身的拟合能力;方差度量了同样大小的训练集的变动所导致的学习性能的变化,即数据扰动造成的影响。【还有一个量叫噪声,表达了当前任务上任何学习算法所能达到的期望泛化误差的下界,刻画了学习问题本身的难度】。
偏差低,对应着模型的参数参数增加和复杂化,此时方差较大,容易过拟合;方差低,对应着模型参数的减小和简单化,此时偏差较高,容易欠拟合。下图给出了偏差方差和总体泛化误差的示意图,两者的冲突明显,称之为偏差方差困境。
解决偏差和方差问题的思路,对于偏差,自然就是寻找更具代表性的特征或者是增大输入向量维度,对于方差,则应该增加数据集合,减少数据维度,使用正则化方法和交差验证法
提到偏差和方差,也不得不提集成学习中的bagging和boosting。bagging是booststrap aggregating的简称,再取样然后在每个样本上训练出的模型取平均,降低的是模型的方差,先天并行的算法都有这个效果比如随机森林;boosting则是迭代算法,每一次迭代根据上一次迭代的预测结果对样本进行加权,所以随着迭代进行,误差会越来越小,这种算法无法并行。简单来说,bagging相当于队训练数据作一定程度的扰动,造成基分类器的多样性,由于基分类器的优化的目标本质上是一致的,所以防擦好会随着集成过程的进行而降低。boosteing表面也是对训练数据的扰动,但是集成分类器具有一个优化目标,本质上是单个优化算法,训练过程可以使集成分类器收敛到最优贝叶斯决策,因此降低了bias。
有的书中也提到,bagging是对许多强分类器求平均,本身每个分类器bias就很低,平均之后仍然低,没什么变化,但是原来的单个分类器强到可能过拟合,即方差高,求平均的操作就能够降低方差。而boosting是把许多弱分类器组合成一个强分类器,弱分类器bias高,强分类器bias低,所以说boosting起到了降低bias的作用,这里variance并不是boosting的主要考虑因素。
2. 预备知识
话题回到讲义本身,该节要学习的是学习理论,在此之前先做一些准备。
首先看两个简单的辅助定理,第一个,联合界引理:

第二个定理,概率论中的霍夫丁不等式,给出了随机变量的和与其期望值偏差的概率上限,学习理论中称为切诺夫界,:
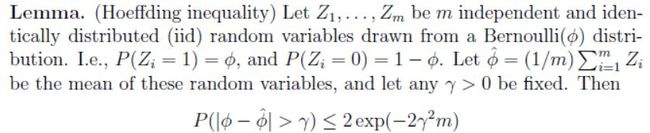
使用这两个简单的定理,我们可以证明学习理论中很多问题,为了简化讨论,这里讨论二类问题。给定一个样本数量为 m m m的训练集 S S S,其中训练样本 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)),每个训练样本都来自分布 D D D,对于假设函数 h h h,定义训练误差/经验风险/经验误差为:

这个式子给出的是 h h h错分类的概率,如果要针对特定的训练集,则有:

这个式子描述的是,从分布 D D D中拿出一个样本, h h h错分的概率。
考虑线性分类问题,令:
![]()
我们如何拟合参数 θ \theta θ,一种可行的方法就是最小化训练误差:
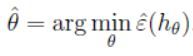
在本节对学习理论的讨论中,我们不再局限于对某个特定的假设函数进行参数拟合,而是定义一个假设类(hypothesis class) H H H,比如说,对于线性分类问题有:
![]()
这里 H H H表示分类器的集合,这里面的分类器都有线性决策边界。
经验风险最小化就可以视为对于一类 H H H进行最小化,这里学习算法可以表示为:
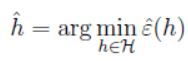
3. H H H为有限集的情况
考虑这样一个学习问题,其中集合 H H H为有限集,包含 k k k个假设函数即:
![]()
H H H包含了 k k k个能将 X X X映射到 { 0 , 1 } \{0,1\} {0,1},经验风险最小化则从中选出训练误差最小的一个。
为了对 h ^ \hat h h^的泛化误差进行分析,分两部分进行,第一部分证明对于所有的 h h h, ε ^ \hat \varepsilon ε^都是对 ε ( h ) \varepsilon(h) ε(h)的一个可靠的估计,第二部分,找出 h ^ \hat h h^的泛化误差的下界。
给定的 h i ∈ H h_i \in H hi∈H,随机变量 Z Z Z服从如下的伯努利分布:取 ( x , y ) ∈ D (x,y)\in D (x,y)∈D,令 Z = 1 { h i ( x ) ≠ y } Z=1\{h_i(x)\neq y\} Z=1{hi(x)=y},也就是 Z Z Z表示假设函数 h i h_i hi是否会错分该样本,同样定义 Z j = 1 { h i ( x ( j ) ) ≠ y ( j ) } Z_j=1\{h_i(x^{(j)})\neq y^{(j)}\} Zj=1{hi(x(j))=y(j)},因为训练集的样本独立同分布服从 D D D,所以 Z Z Z和 Z j Z_j Zj就相同的分布。
可以看到,随机抽取的样本被错分的概率 ε ( h ) \varepsilon(h) ε(h)正好为 Z Z Z和 Z j Z_j Zj的期望,可以写为:

ε ^ ( h i ) \hat \varepsilon(h_i) ε^(hi)恰好是 m m m个服从均值为 ε ( h i ) \varepsilon(h_i) ε(hi)的伯努利分布的随机变量 Z j Z_j Zj的均值,所以这里可以应用霍夫丁不等式得到:
![]()
可以看到,若训练集足够大,对于特定的 d o u h i douh_i douhi,训练误差将有很高的概率和泛化误差接近,但是我们不仅针对单个 h i h_i hi,需要证明对于所有的 h ∈ H h \in H h∈H,都有这个性质。假定 A i A_i Ai代表事件 ∣ ε ( h i ) − ε ^ ( h i ) ∣ > γ |\varepsilon(h_i)-\hat \varepsilon(h_i)|> \gamma ∣ε(hi)−ε^(hi)∣>γ,已经证明对于也顶的 A i A_i Ai,有 P ( A i ) ≤ 2 e x p ( − 2 γ 2 m ) P(A_i) \leq 2 exp(-2\gamma^2m) P(Ai)≤2exp(−2γ2m),所以应用联合界引理。有:

上面的这个结果又被称为均匀收敛结果。通过上面的这些讨论,我们做到了对于特定的 m m m和 γ \gamma γ值,给出 h ∈ H h \in H h∈H, ∣ ε ( h ) − ε ^ ( h ) ∣ > γ |\varepsilon(h)-\hat \varepsilon(h)|>\gamma ∣ε(h)−ε^(h)∣>γ的概率边界,这样 m 、 γ m、\gamma m、γ以及误差的概率三者,给定两者可以确定另外一个。
举个栗子,给定 γ \gamma γ和某个 δ > 0 \delta >0 δ>0, m m m必须为多少才能保证训练误差和泛化误差的差的绝对值小于 γ \gamma γ的概率至少为 1 − δ 1-\delta 1−δ?我们可以,令 δ = 2 k e x p ( − 2 γ 2 m ) \delta=2kexp(-2\gamma^2m) δ=2kexp(−2γ2m)然后解出m,即:

也就是说 m m m至少为这个值,才能保证 1 − δ 1-\delta 1−δ的概率,这个界就给出了训练样本数量的下界来保证泛化误差和训练误差之间的接近程度。这个为保证特定方法的性能而选取的 m m m值也被称为算法的抽样复杂度。而且这个界仅仅是假设类 H H H的数量 k k k的对数。
同样,我们也可以固定 m m m和 γ \gamma γ,来对 γ \gamma γ求解,给出概率 1 − δ 1-\delta 1−δ,可以得到:
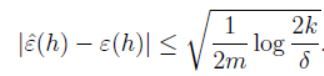
定义 h ∗ = a r g m i n h ∈ H ε ^ ( h ) h^*=argmin_{h \in H} \hat \varepsilon(h) h∗=argminh∈Hε^(h)为假设类 H H H中效果最好的一个函数,则有下面的不等式:
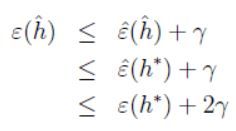
综合上面的式子,我们可以得出这样一个式子(固定的 m 、 δ m、\delta m、δ),概率至少为 1 − δ 1-\delta 1−δ,有:

假如我们现在有一个更大的假设类 H ′ H' H′,那么上式的第一部分必定不增,偏差同样也必定不会增加;但是如果 k k k增加了,那么第二部分可能会增加,这也对应着方差的增加。
给定 γ \gamma γ和 δ \delta δ,并且像之前一样求解 m m m,我们可以得到下面的取样复杂度边界:
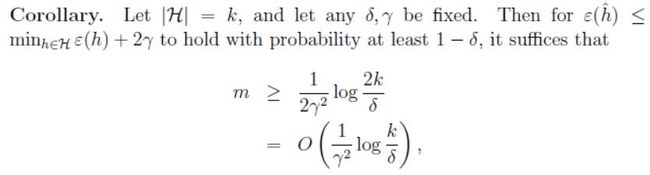
4. H H H为无限集的情况
上面证明了一些 H H H为有限集的定理,但是对于许多假设类,可能包含任意的实参数,也就是说假设类中假设函数的数量任意大时,我们是否能得到相同的结论?
令假设类 H H H有 d d d个实参给出,那么在现有的硬件条件下,假设类 H H H中 k = 2 64 d k=2^{64d} k=264d,这样一来,为了保证 ε ( h ^ ) ≤ ε ( h ∗ ) + 2 γ \varepsilon(\hat h) \leq \varepsilon(h^*)+2\gamma ε(h^)≤ε(h∗)+2γ的概率至少为 1 − δ 1-\delta 1−δ,那么必须满足:
![]()
但是上面的结论还是存在限制条件的,为了进一步推进讨论,给出下面的一些定义:
给定一个点的集合 S = { x ( i ) , . . . , x ( d ) } S=\{x^{(i)},...,x^{(d)}\} S={x(i),...,x(d)}(和训练集没有关系),其中 x ( i ) ∈ X x^{(i)} \in X x(i)∈X,如果 H H H可以实现对集合 S S S的任意标签化,那么称 H H H打散 S S S,比如,对于任一标签集合{ y ( 1 ) , . . . , y ( d ) y^{(1)},...,y^{(d)} y(1),...,y(d)},在 H H H中都存在 h h h使得 h ( x ( i ) ) = y ( i ) h(x^{(i)})=y^{(i)} h(x(i))=y(i)。
给定一个假设类 H H H,定义它的VC维为它能打散的最大的集合,若能打散任意集合,则 V C ( H ) = ∞ VC(H)=∞ VC(H)=∞,考虑下面这样一个有三个点的集合:

那么二维的线性分类器集合 H , ( h ( x ) = 1 { θ 0 + θ 1 x 1 + θ 2 x 2 ≥ 0 } ) H,(h(x)=1\{\theta_0+\theta_1x_1+\theta_2x_2\geq0\}) H,(h(x)=1{θ0+θ1x1+θ2x2≥0})能打散上面的集合吗?答案时肯定的,下面的八种情况我们都可以找到没有分类误差的线性分类器:

然而这个假设类不能打散有4个点的集合,因此假设类的VC维为3。
但是也存在这个假设类不能打散的三个点的集合,比如下面的情况
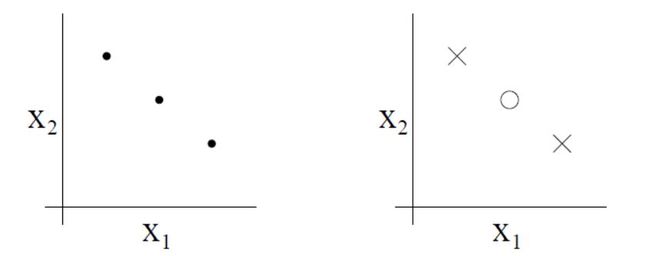
也就是说概率至少为 1 − δ 1-\delta 1−δ时我们有:

换句话说,如果假设类的VC维有限,那么均匀收敛的结果可能 m m m会很大,这样就可以给出训练误差的一个界,这样我们有如下推论:
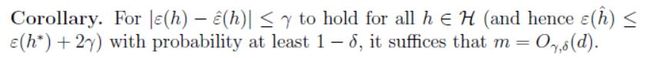
也就是说,假设类能够训练好所必须的训练样本的数量和VC维有线性惯性,对于多数的假设类,它的VC维和参数数量也有线性关系。综合起来,我们可以得出结论,算法如果想要最小化训练误差,那么训练集样本的数量通常和假设类中参数的数量大致有线性关系。【没想到我们的直觉要证明是需要这么多东西的/(ㄒoㄒ)/~~】
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
![]()

