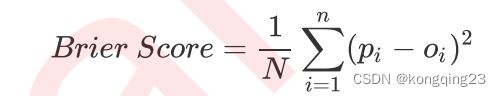机器学习sklearn-朴素贝叶斯2

目录

概率类模型的评估指标

布里尔分数Brier Score

对数损失

可靠性曲线

预测概率的直方图

多项式朴素贝叶斯

sklearn中的多项式贝叶斯

伯努利朴素贝叶斯

朴素贝叶斯的样本不均衡问题 

补集朴素贝叶斯

贝叶斯作文本分类

---

概率类模型的评估指标

混淆矩阵和精确性可以帮助我们了解贝叶斯的分类结果。然而，我们选择贝叶斯进行分类，大多数时候都不是为了单单追求效果，而是希望看到预测的相关概率。这种概率给出预测的可信度，所以对于概率类模型，我们希望能够由其他的模型评估指标来帮助我们判断，模型在“概率预测 ”这项工作上，完成得如何。

布里尔分数Brier Score

概率预测的准确程度被称为 “ 校准程度 ” ，是衡量算法预测出的概率和真实结果的差异的一种方式。一种比较常用的指标叫做布里尔分数，它被计算为是概率预测相对于测试样本的均方误差，表示为：

这个指标衡量了我们的概率距离真实标签结果的差异，其实看起来非常像是均方误差。 布里

尔分数的范围是从 0 到 1 ，分数越高则预测结果越差劲，校准程度越差，因此布里尔分数越接近 0 越好 。由于它的本质也是在衡量一种损失，所以在sklearn 当中，布里尔得分被命名为 brier_score_loss 。

注意：新版sklearn的布里尔分数只支持二分类数据。

 

对数损失

另一种常用的概率损失衡量是对数损失（ log_loss ），又叫做对数似然，逻辑损失或者交叉熵损失，它是多元逻辑回归以及一些拓展算法，比如神经网络中使用的损失函数。它被定义为，对于一个给定的概率分类器，在预测概率为条件的情况下，真实概率发生的可能性的负对数。由于是损失，因此对数似然函数的取值越小，则证明概率估计越准确，模型越理想 。值得注意得是， 对数损失只能用于评估分类型模型。

 

 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import brier_score_loss
from sklearn.metrics import log_loss
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

X = load_digits().data
y = load_digits().target
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3,random_state = 0)

estimators = [GaussianNB().fit(Xtrain,Ytrain)
             ,LR(solver = 'lbfgs',max_iter = 3000,multi_class = 'auto').fit(Xtrain,Ytrain)
             ,SVC(kernel = 'rbf').fit(Xtrain,Ytrain)
             ]
name = ['GaussianNB','LogisticRegression','SVC']

for i,estimator in enumerate(estimators):
    if hasattr(estimator,'predict_proba'): #查看是否存在概率属性
        prob = estimator.predict_proba(Xtest)
        print("{}'s log_loss is:{}\n".format(name[i],log_loss(Ytest,prob)))
    else: #不存在则进行归一化处理
        prob = (estimator.decision_function(Xtest) - estimator.decision_function(Xtest).min())\
               /(estimator.decision_function(Xtest).max()-estimator.decision_function(Xtest).min())
        print("{}'s log_loss is:{}\n".format(name[i],log_loss(Ytest,prob)))

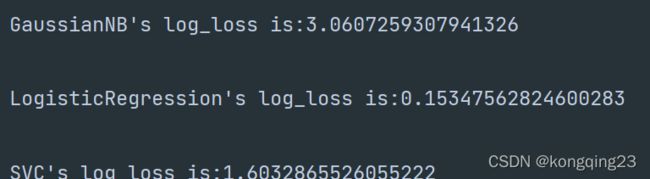
我们用 log_loss 得出的结论和我们使用布里尔分数得出的结论不一致 ：当使用布里尔分数作为评判标准的时候，SVC 的估计效果是最差的，逻辑回归和贝叶斯的结果相接近。而使用对数似然的时候，虽然依然是逻辑回归最强大，但贝叶斯却没有SVC 的效果好。为什么会有这样的不同呢？

因为逻辑回归和 SVC 都是以最优化为目的来求解模型，然后进行分类的算法。而朴素贝叶斯中，却没有最优化的过程。对数似然函数直接指向模型最优化的方向，甚至就是逻辑回归的损失函数本身，因此在逻辑回归和SVC 上表现得更好。

在现实应用中，对数似然函数是概率类模型评估的黄金指标，往往是我们评估概率类模型的优先选择。但是它也有一些缺点，首先它没有界，不像布里尔分数有上限，可以作为模型效果的参考。其次，它的解释性不如布里尔分数，很难与非技术人员去交流对数似然存在的可靠性和必要性。第三，它在以最优化为目标的模型上明显表现更好。而且，它还有一些数学上的问题，比如不能接受为0 或 1 的概率，否则的话对数似然就会取到极限值。

 

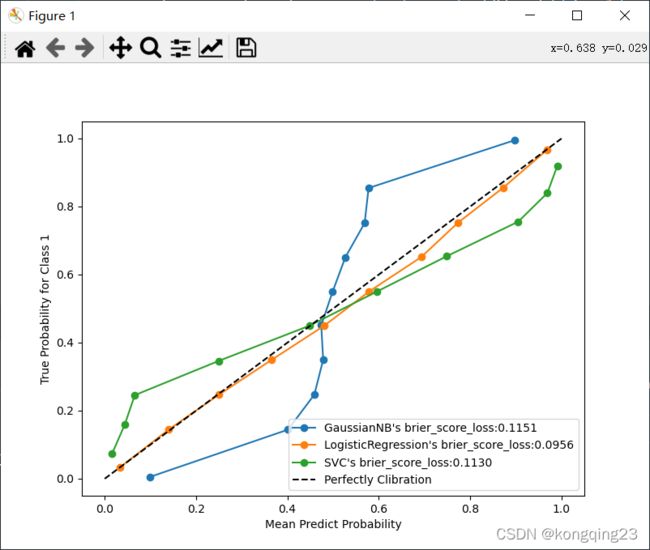
可靠性曲线

可靠性曲线（ reliability curve ），又叫做概率校准曲线（ probability calibration curve ），可靠性图（ reliability diagrams），这是一条以预测概率为横坐标，真实标签为纵坐标的曲线。我们希望预测概率和真实值越接近越好，最好两者相等，因此一个模型 / 算法的概率校准曲线越靠近对角线越好 。校准曲线因此也是我们的模型评估指标之 一。和布里尔分数相似，概率校准曲线是对于标签的某一类来说的，因此一类标签就会有一条曲线，或者我们可以使用一个多类标签下的平均来表示一整个模型的概率校准曲线。但通常来说，曲线用于二分类的情况最多。

 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification as mc
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.metrics import brier_score_loss
from sklearn.calibration import calibration_curve
from sklearn.model_selection import train_test_split

#创建二分类数据
X, y = mc(n_samples=100000, n_features=20  # 总共20个特征
          , n_classes=2  # 标签为2分类
          , n_informative=2  # 其中两个代表较多信息
          , n_redundant=10  # 10个都是冗余特征
          , random_state=42)

#样本量足够大 10%作为训练集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.9, random_state=0)

estimators = [GaussianNB().fit(Xtrain, Ytrain)
    , LR(solver='lbfgs', max_iter=3000, multi_class='auto').fit(Xtrain, Ytrain)
    , SVC(kernel='rbf').fit(Xtrain, Ytrain)
              ]

fig, ax = plt.subplots(figsize=(8, 6))
name = ['GaussianNB', 'LogisticRegression', 'SVC']
for i, estimator in enumerate(estimators):
    if hasattr(estimator, 'predict_proba'):
        proba = estimator.predict_proba(Xtest)[:, 1]
    else:
        prob = estimator.decision_function(Xtest)
        proba = (prob - prob.min()) / (prob.max() - prob.min())

    trueproba, predproba = calibration_curve(Ytest, proba, n_bins=10)
    bls = brier_score_loss(Ytest, proba, pos_label=1)
    ax.plot(trueproba, predproba, 'o-', label='{}\'s brier_score_loss:{:.4f}'.format(name[i], bls))
ax.set_xlabel('Mean Predict Probability')
ax.set_ylabel('True Probability for Class 1')
ax.set_ylim(-0.05, 1.05)
ax.plot([0, 1], [0, 1], '--', c='k', label='Perfectly Clibration')
ax.legend(loc='best')
plt.show()

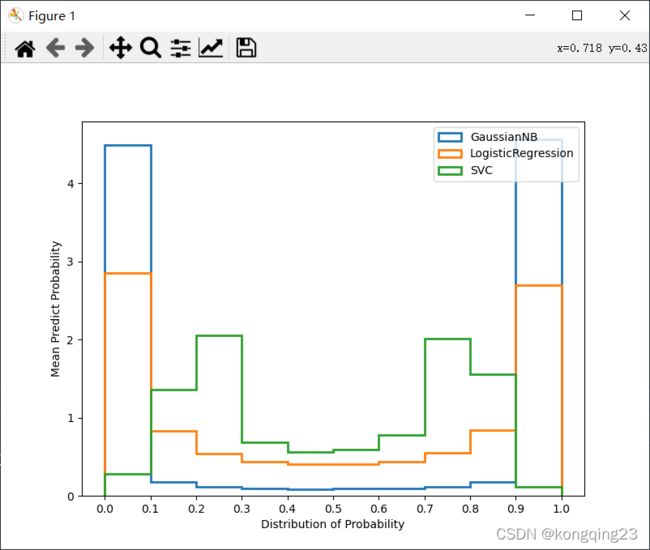
预测概率的直方图

直方图是以样本的预测概率分箱后的结果为横坐标，每个箱中的样本数量为纵坐标的一个图像。注意，这里的分箱和我们在可靠性曲线中的分箱不同，这里的分箱是将预测概率均匀分为一个个的区间，与之前可靠性曲线中为了平滑的分箱完全是两码事。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification as mc
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.metrics import brier_score_loss
from sklearn.calibration import calibration_curve
from sklearn.model_selection import train_test_split

#创建二分类数据
X, y = mc(n_samples=100000, n_features=20  # 总共20个特征
          , n_classes=2  # 标签为2分类
          , n_informative=2  # 其中两个代表较多信息
          , n_redundant=10  # 10个都是冗余特征
          , random_state=42)

#样本量足够大 10%作为训练集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.9, random_state=0)

estimators = [GaussianNB().fit(Xtrain, Ytrain)
    , LR(solver='lbfgs', max_iter=3000, multi_class='auto').fit(Xtrain, Ytrain)
    , SVC(kernel='rbf').fit(Xtrain, Ytrain)
              ]

fig,ax1 = plt.subplots(figsize = (8,6))
name = ['GaussianNB','LogisticRegression','SVC']

for i,estimator in enumerate(estimators):
    if hasattr(estimator,'predict_proba'):
        proba = estimator.predict_proba(Xtest)[:,1]
    else:
        prob = estimator.decision_function(Xtest)
        proba = (prob-prob.min())/(prob.max()-prob.min())
    ax1.hist(proba
            ,bins=10
            ,label=name[i]
            ,histtype="step" #设置直方图为透明
            ,lw=2 #设置直方图每个柱子描边的粗细
            ,density = True
            )
ax1.set_xlabel('Distribution of Probability')
ax1.set_ylabel('Mean Predict Probability')
ax1.set_xlim([-0.05, 1.05])
ax1.set_xticks([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1])
ax1.legend()
plt.show()

多项式朴素贝叶斯

多项式贝叶斯可能是除了高斯之外，最为人所知的贝叶斯算法了。它也是基于原始的贝叶斯理论，但假设概率分布是服从一个简单多项式分布。多项式分布来源于统计学中的多项式实验，这种实验可以具体解释为：实验包括n 次重复试验，每项试验都有不同的可能结果。在任何给定的试验中，特定结果发生的概率是不变的。

多项式分布擅长的是分类型变量。

多项式实验中的实验结果都很具体，它所涉及的特征往往是次数，频率，计数，出现与否这样的概念，这些概念都是离散的正整数，因此sklearn 中的多项式朴素贝叶斯不接受负值的输入 。

sklearn中的多项式贝叶斯

from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB #多项式朴素贝叶斯
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss
import numpy as np

#数据样本为500
class_1=500
class_2=500
centers=[[0.0,0.0],[2.1,2.1]]
cluster_std=[0.5,0.5]
X,y=make_blobs(n_samples=[class_1,class_2],
               centers=centers,
               cluster_std=cluster_std,
               random_state=10,shuffle=False#不打乱数据集
               )
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                               ,test_size=0.3
                                               ,random_state=420)
#归一化 确保特征矩阵不存在负值
#多项式贝叶斯不接受负值
mms=MinMaxScaler().fit(Xtrain)
Xtrain=mms.transform(Xtrain)
Xtest=mms.transform(Xtest)



#建立多项式贝叶斯分类器
mnb=MultinomialNB().fit(Xtrain,Ytrain)
print(mnb.class_log_prior_)#查看每个标签类的对数先验概率 永远是负数
print(np.exp(mnb.class_log_prior_))#查看真正的概率值
print(mnb.score(Xtest,Ytest))
#[-0.69029411 -0.69600841]
#[0.50142857 0.49857143]
#0.49666666666666665

#将连续型变量离散化后分箱查看准确性
kbs=KBinsDiscretizer(n_bins=10,encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb_=MultinomialNB().fit(Xtrain_,Ytrain)
print(mnb_.score(Xtest_,Ytest))
#0.9933333333333333

伯努利朴素贝叶斯

多项式朴素贝叶斯可同时处理二项分布（抛硬币）和多项分布（掷骰子），其中二项分布又叫做伯努利分布，它是一 种现实中常见，并且拥有很多优越数学性质的分布。因此，既然有着多项式朴素贝叶斯，我们自然也就又专门用来处理二项分布的朴素贝叶斯：伯努利朴素贝叶斯。

 

伯努利贝叶斯类 BernoulliN 假设数据服从多元伯努利分布，并在此基础上应用朴素贝叶斯的训练和分类过程。多元伯努利分布简单来说，就是数据集中可以存在多个特征，但每个特征都是二分类的，可以以布尔变量表示，也可以表示为{0 ， 1} 或者 {-1 ， 1} 等任意二分类组合。因此，这个类要求将样本转换为二分类特征向量，如果数据本身不是二分类的，那可以使用类中专门用来二值化的参数binarize 来改变数据。

伯努利朴素贝叶斯与多项式朴素贝叶斯非常相似，都常用于处理文本分类数据。但由于伯努利朴素贝叶斯是处理二项分布，所以它更加在意的是“ 存在与否 ” ，而不是 “ 出现多少次 ” 这样的次数或频率，这是伯努利贝叶斯与多项式贝叶斯的根本性不同。

朴素贝叶斯的样本不均衡问题 

from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.metrics import brier_score_loss as BS,recall_score,roc_auc_score as AUC

class_1 = 50000 #多数类为50000个样本
class_2 = 500 #少数类为500个样本
centers = [[0.0, 0.0], [5.0, 5.0]] #设定两个类别的中心
clusters_std = [3, 1] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)

name = ["Multinomial","Gaussian","Bernoulli"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB()]
for name,clf in zip(name,models):
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
    #不是高斯分布则需要进行分箱离散化处理
    if name != "Gaussian":
         kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
         Xtrain = kbs.transform(Xtrain)
         Xtest = kbs.transform(Xtest)

    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    proba = clf.predict_proba(Xtest)[:,1]
    score = clf.score(Xtest,Ytest)
    print(name)
    print("\tBrier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
    print("\tAccuracy:{:.3f}".format(score))
    print("\tRecall:{:.3f}".format(recall_score(Ytest,y_pred)))
    print("\tAUC:{:.3f}".format(AUC(Ytest,proba)))
    
"""
    Multinomial
	Brier:0.007
	Accuracy:0.990
	Recall:0.000
	AUC:0.991
Gaussian
	Brier:0.006
	Accuracy:0.990
	Recall:0.438
	AUC:0.993
Bernoulli
	Brier:0.009
	Accuracy:0.987
	Recall:0.771
	AUC:0.987
"""

从结果上来看，多项式朴素贝叶斯判断出了所有的多数类样本，但放弃了全部的少数类样本，受到样本不均衡问题影响最严重。高斯比多项式在少数类的判断上更加成功一些，至少得到了43.8% 的 recall 。伯努利贝叶斯虽然整体的准确度和布里尔分数不如多项式和高斯朴素贝叶斯和，但至少成功捕捉出了77.1% 的少数类。可见，伯努利贝叶斯最能够忍受样本不均衡问题。

补集朴素贝叶斯

补集朴素贝叶斯（ complement naive Bayes ， CNB ）算法是标准多项式朴素贝叶斯算法的改进。 CNB 的发明小组创造出CNB 的初衷是为了解决贝叶斯中的 “ 朴素 ” 假设带来的各种问题，他们希望能够创造出数学方法以逃避朴素贝叶斯中的朴素假设，让算法能够不去关心所有特征之间是否是条件独立的。以此为基础，他们创造出了能够解决样本不平衡问题，并且能够一定程度上忽略朴素假设的补集朴素贝叶斯。在实验中，CNB 的参数估计已经被证明比普通多项式朴素贝叶斯更稳定，并且它特别适合于样本不平衡的数据集。有时候，CNB 在文本分类任务上的表现有时能够优于多项式朴素贝叶斯，因此现在补集朴素贝叶斯也开始逐渐流行。

贝叶斯作文本分类

我们可以通过将文字数据处理成数字数据，然后使用贝叶斯来帮助我们判断一段话，或者一篇文章中的主题分类，感情倾向，甚至文章体裁。现在，绝大多数社交媒体数据的自动化采集，都是依靠首先将文本编码成数字，然后按分类结果采集需要的信息。

在开始分类之前，我们必须先将文本编码成数字。一种常用的方法是单词计数向量。在这种技术中，一个样本可以包含一段话或一篇文章，这个样本中如果出现了10 个单词，就会有 10 个特征 (n=10) ，每个特征代表一个单词，特征的取值表示这个单词在这个样本中总共出现了几次，是一个离散的，代表次数的，正整数 。

如果使用单词计数向量，可能会导致一部分常用词（比如中文中的 ” 的 “ ）频繁出现在我们的矩阵中并且占有很高的权重，对分类来说，这明显是对算法的一种误导。为了解决这个问题，比起使用次数，我们使用单词在句子中所占的比例来编码我们的单词，这就是我们著名的TF-IDF 方法。

TF-IDF 全称 term frequency-inverse document frequency ，词频逆文档频率，是通过单词在文档中出现的频率来衡量其权重，也就是说，IDF 的大小与一个词的常见程度成反比，这个词越常见，编码后为它设置的权重会倾向于越小，以此来压制频繁出现的一些无意义的词。

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer as TFIDF
from sklearn.datasets import fetch_20newsgroups
from sklearn.naive_bayes import MultinomialNB, ComplementNB, BernoulliNB
from sklearn.metrics import brier_score_loss as BS
import pandas as pd
import numpy as np

#初次使用这个数据集的时候，会在实例化的时候开始下载
data = fetch_20newsgroups()

#提取4钟类型数据
categories = ["sci.space" #科学技术 - 太空
              ,"rec.sport.hockey" #运动 - 曲棍球
              ,"talk.politics.guns" #政治 - 枪支问题
              ,"talk.politics.mideast"] #政治 - 中东问题

train = fetch_20newsgroups(subset="train",categories = categories)
test = fetch_20newsgroups(subset="test",categories = categories)

#提取训练集测试集
Xtrain = train.data
Xtest = test.data
Ytrain = train.target
Ytest = test.target
#使用TFIDF编码
tfidf=TFIDF().fit(Xtrain)
Xtrain_=tfidf.transform(Xtrain)
Xtest_ = tfidf.transform(Xtest)

name = ["Multinomial","Complement","Bournulli"]
#注意高斯朴素贝叶斯不接受稀疏矩阵
models = [MultinomialNB(),ComplementNB(),BernoulliNB()]

for name,clf in zip(name,models):
    clf.fit(Xtrain_,Ytrain)
    y_pred = clf.predict(Xtest_)
    proba = clf.predict_proba(Xtest_)
    score = clf.score(Xtest_,Ytest)
    print(name)
    #4个不同的标签取值下的布里尔分数
    Bscore = []
    for i in range(len(np.unique(Ytrain))):
        bs = BS(Ytest==i,proba[:,i],pos_label=i)
        Bscore.append(bs)
        print("\tBrier under {}:{:.3f}".format(train.target_names[i],bs))
    print("\tAverage Brier:{:.3f}".format(np.mean(Bscore)))
    print("\tAccuracy:{:.3f}".format(score))
    print("\n")
    
    """ 
        Multinomial
	Brier under rec.sport.hockey:0.857
	Brier under sci.space:0.033
	Brier under talk.politics.guns:0.169
	Brier under talk.politics.mideast:0.178
	Average Brier:0.309
	Accuracy:0.975


Complement
	Brier under rec.sport.hockey:0.804
	Brier under sci.space:0.039
	Brier under talk.politics.guns:0.137
	Brier under talk.politics.mideast:0.160
	Average Brier:0.285
	Accuracy:0.986


Bournulli
	Brier under rec.sport.hockey:0.925
	Brier under sci.space:0.025
	Brier under talk.politics.guns:0.205
	Brier under talk.politics.mideast:0.193
	Average Brier:0.337
	Accuracy:0.902
    """