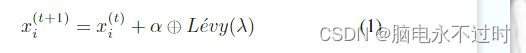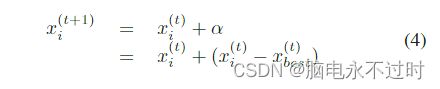用于旅行商问题的离散布谷鸟算法
英文:Discrete Cuckoo Search for Traveling Salesm Problem
摘要
杜鹃搜索(CS)属于一类新颖的自然启发算法,其灵感来源于一些杜鹃物种的专性卵寄生,将它们的卵放在其他寄主鸟类(其他物种)的巢穴中。CS已成功地应用于解决连续优化问题,但其在离散问题中的潜力尚未得到充分的探索。本文在现有CS算法的基础上,构造了一个离散杜鹃搜索(DCS)来求解旅行销售问题(TSP)。研究了两种方案,即离散步长和杜鹃的更新方案。与其他方法相比,DCS在TSP问题上进行了评估。实验结果表明,所提出的算法能够很好地解决一些TSP实例,但对于一些其他实例,它可能会陷入局部最优解。
1. 介绍
旅行销售问题(TSP)被称为传统上难以解决的经典优化问题之一。这个问题在1930年被表述为数学问题,是世界上研究最为深入的问题之一。基本上,在这种情况下,销售人员需要一次访问每个城市,然后从旅行的起点返回城市。该问题的精确解决将涉及算法,这些算法需要寻求所有现有解决方案的可能性,因此该问题也属于非确定性多项式经济完整性(NPComplete)问题([1],[2],[3]),并已证明没有在多项式时间运行的方案或算法来解决TSP[4]。因此,该算法的执行时间经济复杂度将与给定输入的大小成指数关系。关于这一研究领域的全面概述,请参见【5】。
已经开发了许多方法来解决TSP,如启发式搜索[6]、神经计算网络[7]和动态规划[8],但进化计算尤其是元启发式算法显示出解决TSP等全局优化问题的一个非常有前途的方向。许多已发表的求解TSP的方法、Luciana Buriol提出的模因算法(已经开发了许多方法来解决TSP,如启发式搜索[6]、神经计算网络[7]和动态规划[8],但进化计算尤其是元启发式算法显示出解决TSP等全局优化问题的一个非常有前途的方向。许多已发表的求解TSP的方法、Luciana Buriol提出的模因算法(memetic algorithm)[9]、Salmani Niasar提出的离散模糊粒子群优化[10]、Marcin L.Pilat提出的遗传算法与蚁群系统相结合[11]、,使用Li Pei Wong[12]提出的基于频率的修剪改进了蜂群优化,以及Huai Kuang Tsai[13]提出的称为异质选择进化算法(HeSEA)的先进方法。这些研究人员提出了将元启发式算法与局部搜索或其他元启发式方法相结合的方法。在[9]、[10]、[11]和[12]中,研究人员专注于具有数百个城市(节点)的小型TSP。通常,当产生的解非常接近已知的最优解时,方法的精度非常高。在[13]中,研究人员关注了拥有数千个城市的大型TSP。他们提出的称为HeSEA的方法能够解决多达3038个城市的TSP,与已知的最优解相比,偏差为0%。它还解决了13509个城市的TSP,偏差仅为0.74%)[9]、Salmani Niasar提出的离散模糊粒子群优化[10]、Marcin L.Pilat提出的遗传算法与蚁群系统相结合[11]、,使用Li Pei Wong[12]提出的基于频率的修剪改进了蜂群优化,以及Huai Kuang Tsai[13]提出的称为异质选择进化算法(HeSEA)的先进方法。这些研究人员提出了将元启发式算法与局部搜索或其他元启发式方法相结合的方法。在[9]、[10]、[11]和[12]中,研究人员专注于具有数百个城市(节点)的小型TSP。通常,当产生的解非常接近已知的最优解时,方法的精度非常高。在[13]中,研究人员关注了拥有数千个城市的大型TSP。他们提出的称为HeSEA的方法能够解决多达3038个城市的TSP,与已知的最优解相比,偏差为0%。它还解决了13509个城市的TSP,偏差仅为0.74%。
杜鹃搜索(CS)是Xin She Yang和SuashDeb[14]开发的自然启发元启发式算法之一,最初设计用于解决持续优化问题。CS获得的最优解远优于通过高效粒子群优化和遗传算法获得的最佳解[15]。在本研究中,提出了离散CS(DCS)来解决TSP。研究了两种方案,即离散步长和解更新方案。本研究集中于CS的简单形式,不与任何其他方法相结合。这里研究的一些TSP实例是拥有666个城市的小型TSP实例。
二,预备知识
A、levy飞行
在自然界中,动物以随机或准随机的方式寻找食物。一般来说,动物的觅食路径实际上是随机行走,因为下一次移动是基于当前位置/状态和到下一个位置的转移概率。它选择哪一个方向隐含地取决于可以用数学建模的概率。各种研究表明,许多动物和昆虫的飞行行为证明了levy飞行的典型特征[16]。Levy飞行是一种随机行走,其中步长根据重尾heavy-tailed概率分布分布。经过大量步数后,距离随机游动原点的距离趋于稳定分布。
B、布谷鸟算法
自然启发的方法是优化问题最强大的算法之一。CS是一种新颖的自然启发算法,灵感来自一些杜鹃物种的专性卵寄生,将它们的卵放在其他寄主鸟类(其他物种)的巢穴中。一些寄主鸟类可以和入侵的杜鹃发生直接冲突。例如,如果一只寄主鸟发现这些蛋不是自己的,它要么扔掉这些外来蛋,要么干脆放弃自己的巢穴,在其他地方建一个新的巢穴。一些杜鹃物种,如新世界的寄生杜鹃,其进化方式使得雌性寄生杜鹃可以模仿少数选定寄主物种的卵的颜色和图案。这降低了卵子被遗弃的概率,从而提高了它们的繁殖能力[18]。值得一提的是,几只寄主鸟与入侵的杜鹃发生了直接冲突。在这种情况下,如果寄主鸟发现蛋不是自己的,它们要么将蛋扔掉,要么干脆放弃自己的巢穴,在其他地方建立新的巢穴。寄生杜鹃经常选择寄主鸟刚刚产卵的巢穴。一般来说,杜鹃鸟卵孵化的时间略早于寄主卵。一旦第一只杜鹃雏鸟孵化出来,它的第一本能反应就是盲目地将寄主的蛋推出巢穴,从而将寄主蛋赶走。这一行动导致杜鹃雏鸟在其宿主鸟提供的食物中所占份额增加[18]。此外,研究表明,杜鹃雏鸟可以模仿寄主雏鸟的叫声,以获得更多的喂食机会。
通过理想化一些杜鹃的专性繁殖寄生,XinShe Yang和Suash Deb于2009年开发了杜鹃启发算法[15]。CS使用以下表示:巢中的每个蛋代表一个解决方案,而布谷鸟蛋代表一种新的解决方案。目的是使用新的、可能更好的解决方案(杜鹃鸟)来替代巢穴中不太好的解决方案。在最简单的形式中,每个巢有一个蛋。该算法可以扩展到更复杂的情况,其中每个巢都有代表一组解的多个蛋。CS基于三个理想化规则:
1)每只杜鹃一次产一个蛋,然后把蛋倒在一个随机选择的窝里
2) 最好的窝和高质量的蛋将传给下一代
3) 可用寄主巢穴的数量是固定的,杜鹃产卵的概率为Pa∈ (0,1)。在这种情况下,寄主鸟可以摆脱蛋,或者干脆放弃巢穴,建立一个全新的巢穴。
为了简单起见,最后一个假设可以近似为n个巢穴的pa部分被新的巢穴替换,具有新的随机解。对于最大化问题,解的质量或适合度可以简单地与目标函数的值成比例。其他形式的适应度可以以类似于遗传算法中的适应度函数的方式定义。
在原始CS中,在迭代t处,根据以下运动方程更新每个杜鹃的位置:
其中α>0是步长,该步长应与兴趣问题的尺度相关,并可由用户选择。在大多数情况下,α=O(1)。上述方程本质上是随机行走的随机方程。一般来说,随机游走是马尔可夫链,其下一状态/位置仅取决于当前位置(上述等式中的第一项)和转移概率(第二项)。符号⊕ 表示入口乘法[19]。这种入门符号类似于PSO中使用的符号,但在这里,通过Levy飞行的随机行走在探索搜索空间方面更有效,因为从长远来看,它的步长要长得多。利维飞行基本上提供了随机行走,而随机步长是从levy分布中得出的。
其具有无穷的方差和无穷的平均值。在这里,布谷鸟的连续跳跃/步长基本上形成了一个随机行走过程,具有幂律步长分布和重尾。
基于[14]和[19],CS在找到具有高成功率的全局最优值方面非常有效。XinShe Yang的模拟表明,CS在效率和成功率方面都优于PSO和GA[15]。这些事实为研究如何在求解TSP中优化CS提供了启发。挑战在于如何设计杜鹃的更新方案。
三、离散布谷鸟
A、布谷鸟的含义
TSP的解表示是如图1所示的排列表示。在这种情况下,蛋、巢或杜鹃没有区别,因为每个巢对应一个蛋,也代表一只杜鹃。这里,杜鹃代表一种解决方案。在遗传算法中,它就像一条代表个体的染色体。在这种表示法中,数组的一个元素代表一个城市(节点),索引代表一次旅行的顺序。
B、离散步长
在连续优化问题[15]中,步长(α)与所关注问题的规模有关。在大多数情况下,α>0或α=1。对于TSP,杜鹃的步长可以定义为杜鹃与同代最佳杜鹃之间的距离。步长方程现在可以表示为:
任意两个杜鹃i和j之间的距离可以定义为它们之间不同弧的数量。在图2中,杜鹃ii中的三个弧12-7、6-15和5-11在杜鹃j中不存在。因此,杜鹃i和杜鹃j之间的不同弧的数目为三。
C、 基于全局的更新方案
在原始CS中,每只杜鹃都用一个步长α和一个随机步长进行更新,该步长是从称为Levy飞行的Levy分布中提取的。在我们的方法中,我们不使用Levy飞行(Levy飞行=1)。CS更新方程式现在可以用以下公式表示:
对于最佳杜鹃的更新方案,通过使用局部随机游走来围绕最佳解进行开发
其中εt是[0,n/2]中的随机数发生器,具有均匀分布,这实际上成为标准随机游走。其中n是城市总数。从快速查看来看,在解决方案更新方案中,DCS和爬山之间似乎有一些相似之处。但有显著的不同。DCS是一种基于概率的算法,其方式类似于GA和PSo。
D、多重进化
当布谷鸟更新解决方案时,布谷鸟中的现有解决方案将被更改。由于杜鹃的表示是置换表示,所以我们使用反转突变来表示更新方案。通过反转突变,可以保持已形成的路径,从而不会损坏先前形成的良好路径。
DCS中的杜鹃使用进化策略(ES)概念更新解决方案。随机选择的杜鹃将使用反转突变进行m次更新。首先,染色体上的索引将在携带反转突变后随机选择。换句话说,随机选择的杜鹃将有m个新的解决方案。如果杜鹃所产的蛋被寄主鸟发现,那么更糟糕的杜鹃也会使用反转突变进行m次更新。因此,在一代人结束时,将有2m个新的解决方案,n只最好的杜鹃将被选为新的种群。
E、DCS方案
DCS的方案由以下伪代码说明。首先,每只杜鹃随机生成初始解。随机得到一只杜鹃,然后生成多达m次的新解,并用最好的杜鹃做同样的事情。然后,生成随机实数,如果随机数小于Pa,则找到最差的布谷鸟,并从最差的杜鹃鸟中生成m倍的新解。如果随机数小于Pa,那么在迭代结束时将出现(3m+n−1) 杜鹃。如果随机数大于Pa,那么在迭代结束时将出现(2m+n)只杜鹃。在迭代结束时,将根据下一次迭代的目标函数选择n个最佳杜鹃,并且这种情况将持续到达到最大迭代。
F、选择n个最佳杜鹃
这个过程是为下一代挑选n只最好的杜鹃。这个选择过程必须保证在一代人中,没有任何杜鹃有相同的解决方案。因此,可以保持种群的多样性,并有助于以高概率生成良好的解决方案。
四、实验结果
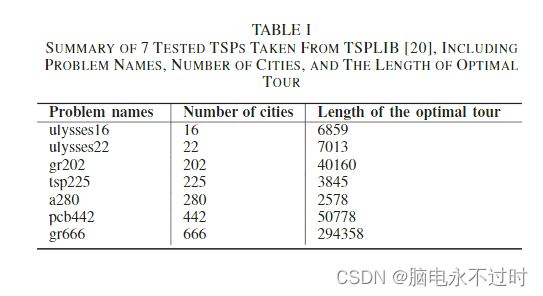
在本研究中,DCS应用于从TSPLIB[20]下载的7个TSP问题。表1列出了问题名称、城市数量和最佳行程长度。在[20]中,TSP实例的类型是欧几里得距离。TSP实例提供了一些城市的坐标。实例名称中的数字表示提供的城市数量。例如,ulysses16提供了16个城市的坐标。问题是,根据欧几里得距离,在每个城市只能参观一次的条件下,参观16个城市的最佳路线是什么。
A、DCS的性能
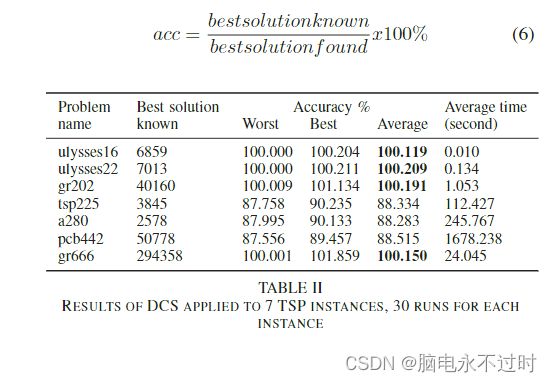
检查DCS以解决7个TSP实例,以查看其性能。在本研究中,DCS使用15只杜鹃的种群大小,进化次数为15。使用这些参数,DCS使用7个TSP实例进行了检验。表2显示了7个实例的最差、最佳和平均精度。通过等式(6)中的公式计算精度。DCS每次运行都能为ulysses16、ulysses22、gr202和gr666提供最佳解决方案。然而,DCS对于tsp225、a280和pcb442这三种情况不是最佳的。
B、 杜鹃种群
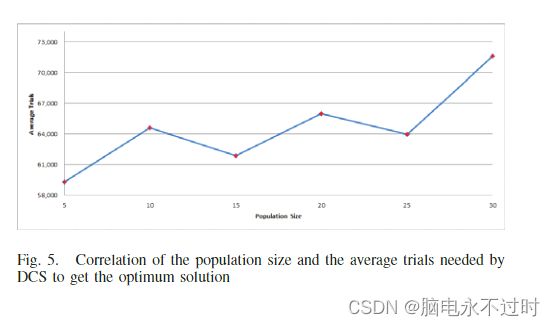
总体规模(n)关键性地决定了计算时间。这里,对问题gr202使用不同的总体规模来测试DCS,以研究其与DCS所需的试验数量的相关性,从而获得最佳解决方案。图5表示了群体规模与达到最佳解决方案的平均试验的相关性(准确率为100%)。平均试验随着人口规模的增加而增加。人口众多并不能保证杜鹃会很快找到最佳的解决方案。根据图5,最佳人口规模为5人。
五、结论
所提出的方法DCS已成功地用于解决TSP。仿真结果表明,该方法对简单TSP具有很好的性能。但是,DCS无法获得复杂TSP的最佳解决方案。理论上,该方法可以与其他技术相结合,如贪婪杜鹃种群的初始化或Lin Kernighan算法,以进一步提高旅游质量