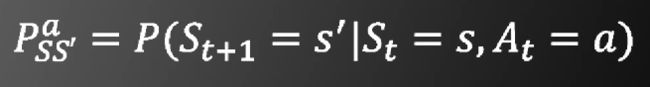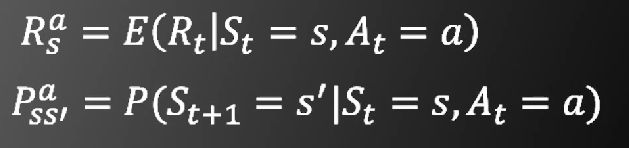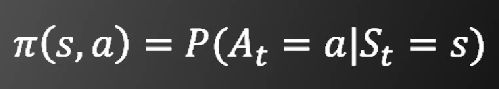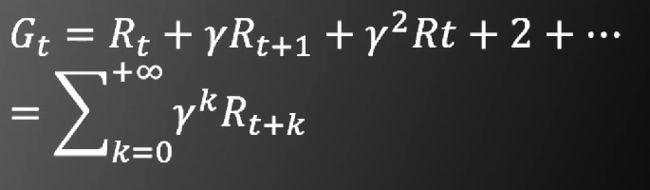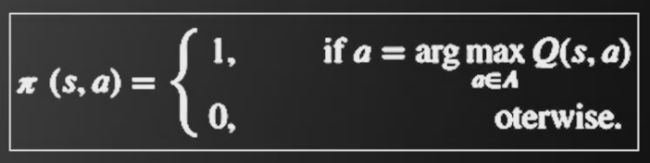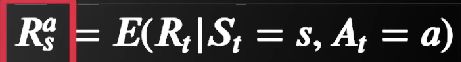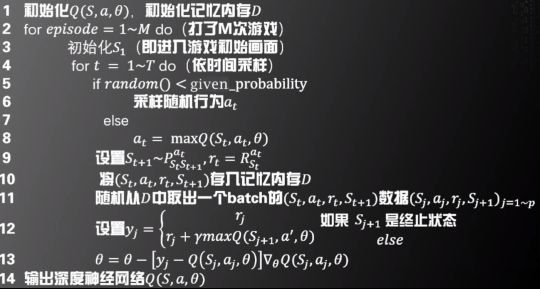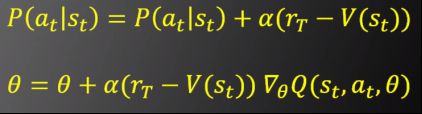【浙江大学机器学习胡浩基】06 强化学习

目录

第一节 Q-Learning和epsion-greedy算法

强化学习与监督学习的区别:

三个假设

1.马尔可夫假设

2.下一个时刻的状态只与这一时刻的状态以及这一时刻的行为有关:

 3.下一个时刻的奖励函数值只与这一时刻的状态及这一时刻的行为有关

 强化学习的过程

 优化目标函数 

 决策机制

定义1:估值函数(Valuel Function) 是衡量某个状态最终能获得多少累计奖励的函数:

定义2:Q函数是衡量某个状态下采取某个行为后，最终能获行得多少累计奖励的函数

 推导过程

 Q-Learning

 epsilon-greedy算法

第二节 深度强化学习

         深度强化学习方向(DEEP REINFORCEMENT LEARNING)

DEEP Q-NETWORKI(DQN)

第三节poicy gradient和actor-critic算法

policy gradient的主要思想

actor-critic算法 

第四节 AphaGo

 AlphaGo原理

AlphaGo Zero 的改进 

---

• 第一节 Q-Learning和epsion-greedy算法

• 强化学习与监督学习的区别:

1.训练数据中没有标签，只有奖励函数(Reward Function)

2.训练数据不是现成给定，而是由行为(Action)获得

3.现在的行为(Action)不仅影响后续训练数据的获得，也影响奖励函数(Reward Function)的取值

4.训练的目的是构建一个“状态->行为”的函数。

状态(State)指目前内部和外部的环境

智能体(Agent)可以通过此函数通函数，决定此时应该采取的行为，最终获得最大的奖励函数值

当然，我们假设状态数和行为数是有限的

• 三个假设

1.马尔可夫假设

2.下一个时刻的状态只与这一时刻的状态以及这一时刻的行为有关:

 

 3.下一个时刻的奖励函数值只与这一时刻的状态及这一时刻的行为有关

 

•  强化学习的过程

在强化学习中已知的函数有

 

需要学习的函数有

 

• 优化目标函数 

增强学习中的待优化目标函数是累积奖励，即一段时间内的奖励函数加权平均值:

这里的gammer是一个衰减项 

•  决策机制

• 定义1:估值函数(Valuel Function) 是衡量某个状态最终能获得多少累计奖励的函数:

• 定义2:Q函数是衡量某个状态下采取某个行为后，最终能获行得多少累计奖励的函数

 

• 推导过程

贝尔曼最优方程(Bellman Optimality Equation)

 

• Q-Learning

这是由于

基于以上定义，可以得出Q-Learning算法如下 

 

获得Q(S,A)后，可用如下式子获得π(s,a)

该算法基本的假设是环境不变，即下面式子的值恒定不变 

但是在实际情况中，这个值是可能发生变化的

为了更好地应对变化，需要在该算法中加入探索和利用(EXPLORATION AND EXPLOITATION)机制

其中

探索表示 稍微偏离目前的最好策略，以便达到搜索更好策略的目的

利用表示 运用目前的最好策略，获取较高的奖赏(Reward)

•  epsilon-greedy算法

以概率epsilon做探索，以概率1-epsilon做利用

具体算法如下

---

• 第二节 深度强化学习

上一节讲到了Q-Learning和epsilon-greedy算法

但是这两个算法存在问题，即状态数和行为数很多时，将会遇到困难。因为以上两个算法需要遍历所有的状态数和行为数，所以状态数和行为数很多时难以求解

深度强化学习方向(DEEP REINFORCEMENT LEARNING)

• DEEP Q-NETWORKI(DQN)

 基本思路:用深度神经网络来模拟 如下图

 即建立一个网络，输入是状态S和行为a，输出是

DQN算法具体流程如下

 

 

---

• 第三节poicy gradient和actor-critic算法

用来解决某一类特定的强化学习任务

这一类任务和前面讲到的强化学习任务有什么区别呢?奖励函数延迟

例如下棋下到最后，才有输和赢;而前面的每一步，虽然有些奖励函数的线索，但与真实输赢的相关性直到最后才能被完全体现。

• policy gradient的主要思想

但是这样会导致算法收敛很慢，而且需要很多数据才能有效。这是因为结果不好，不代表每一个具体过程都不好；结果很好，也不代表每一个具体的过程都很好。这些不准确的因素叠加在一起，就需要大量的数据去平衡，最终使算法收敛

估值函数(VALUE FUNCTION) V(s)

代表在状态s下对最终收益的估计

加入了估值函数后，算法的流程如下

 

• actor-critic算法 

主要思想

具体算法如下 

 

---

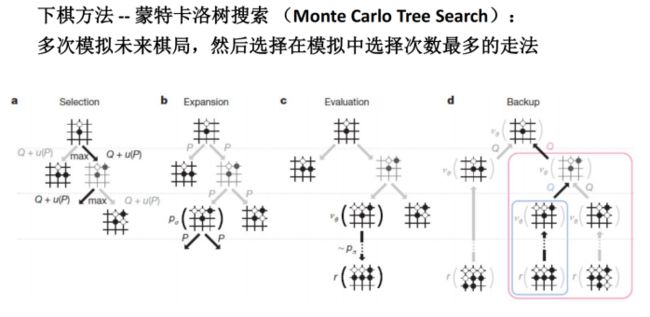
• 第四节 AphaGo

博弈论(GAME THEORY)

一个有限步(N步)完成的零和博弈必有必胜策略

开源代码： https://github.com/Rochester-NRT/RocAlphaGo

相关论文

•  AlphaGo原理

三个深度策略网络 (Policy Networks) 一个深度估值网络(Value Network)

 

 

 

 

 

 

• AlphaGo Zero 的改进