【自然语言处理】【对比学习】SimCSE：基于对比学习的句向量表示

相关博客：
【自然语言处理】【对比学习】SimCSE：基于对比学习的句向量表示
【自然语言处理】BERT-Whitening
【自然语言处理】【Pytorch】从头实现SimCSE
【自然语言处理】【向量检索】面向开发域稠密检索的多视角文档表示学习
【自然语言处理】【向量表示】AugSBERT：改善用于成对句子评分任务的Bi-Encoders的数据增强方法
【自然语言处理】【向量表示】PairSupCon：用于句子表示的成对监督对比学习

一、简介

• 学习通用句嵌入向量是一个NLP的基础问题。本文通过对比学习的方式实现了SOTA句嵌入向量。具体来说，论文提出了称为$\text{SimCSE(Simple Contrastive Sentence Embedding Framework)}$的对比学习框架，可以用于学习通用句嵌入向量。其中$\text{SimCSE}$可以分为“无监督$\text{SimCSE}$”和"有监督$\text{SimCSE}$"。
• 在无监督$\text{SimCSE}$中，仅使用dropout进行数据增强操作。具体来说，将同一个样本输入预训练编码器两次(BERT)，由于每次的dropout是不同的，那么就会生成两个经过dropout后的句向量表示，将这两个样本作为“正样本对”。
• 通过实验发现，使用dropout进行数据增强好于其他常见的数据增强方法，例如：单词删除和替换。可以将dropout看作是最小的数据增强。
• 在有监督$\text{SimCSE}$中，我们基于$\text{NLI}$数据集来构造对比样本，从而实现有监督的对比学习。具体来说，论文将entailment样本作为“正样本对”，并将contradiction样本作为hard“负样本对”。实验表明，$\text{NLI}$数据集对于学习句子表示特别有效。
• 论文进一步分析了两个指标，分别是：正样本对的alignment和表示空间的uniformity。证明了$\text{SimCSE}$能够学习到更好的句子嵌入向量。
• 论文从理论上证明$\text{SimCSE}$改善了uniformity，并将对比学习与近期发现的预训练词向量各向异性联系起来。

二、背景知识

1. 对比学习

【自然语言处理】【对比学习】搞nlp还不懂对比学习，不会吧？快来了解下SimCLR

2. Alignment和Uniformity

Wang等人确定了对比学习的两个关键特性：alignment和uniformity，并提出了衡量这两个特性的评估指标。

2.1 Alignment

给定一个正样本对分布$p_{pos}$，alignment的目标就是计算正样本对嵌入向量的期望距离
$${\ell }_{\text{align}}\triangleq {\mathbb{E}}_{(x,x^{+})\sim p_{pos}}||f(x)-f(x^{+})|{|}^2$$
其中，$f(x)$将样本转换为嵌入向量的编码器。直观来看，alignment越小越好。

2.2 Uniformity

uniformity用于衡量嵌入向量是否有良好的统一分布
$${\ell }_{\text{uniform}}\triangleq \text{log}{\mathbb{E}}_{x,y\sim p_{data}}{e}^{-2||f(x)-f(y)|{|}^2}$$
其中，$p_{data}$表示数据分布。${\ell }_{\text{uniform}}$越小，则两个随机样本的距离也就越大，整个样本的嵌入向量就会越分散。因此，${\ell }_{\text{uniform}}$越小越好。

三、无监督SimCSE

1. 方法

给定一个句子集合$\{x_i{\}}_{i=1}^m$，并且令$x_i^{+}=x_i$。使用独立的dropout作为掩码来进一步获得增强的正样本对。由于在标准的Transformer训练过程中，会有多个dropout掩码。因此，样本的嵌入向量生成表示为${\text{h}}_i^z=f_{\theta }(x_i,z)$，其中$z$是随机的dropout掩码。

$\text{SimCSE}$通过将相同的样本输入的编码器，并应用不同的dropout掩码$z,z^{\prime }$，从而获得相同样本的不同增强样本。最终的对比损失函数为
$${\ell }_i=-\text{log}\frac{e^{sim({\text{h}}_i^{z_i},{\text{h}}_i^{z_i^{\prime }})/\tau }}{{\sum }_{j=1}^N{e}^{sim({\text{h}}_i^{z_i},{\text{h}}_i^{z_j^{\prime }})/\tau }}$$
其中，$N$是随机采样batch的大小。

2. 不同数据增强方式的对比

dropout可以看做是数据增强的最小形式。

我们在$\text{STS-B}$数据集上比较了的dropout数据增强与常见数据增强技术。在这些实验中，语料是从$\text{Wikipedia}$中抽取的，且令$N=512$且$m=10^6$。在表2中可以看到，对比了常见的数据增强技术，例如：crop、word deletion和replacement等。这些数据增强技术的应用可以看着是$\text{h}=f_{\theta }(g(x),z)$，其中$g$是一个在$x$上的离散数据增强操作。

我们的实验发现，即使仅删除一个单词，也是对方法性能有显著影响的。没有任何一种离散数据增强方式由于dropout噪音。

3. dropout进一步实验

这部分的实验如表4所示。

• 为了进一步研究dropout，论文尝试了不同dropout的比例，并发现默认的dropout比率$p=0.1$是效果最好的。
• 在两个极端情况下：$p=0$(没有进行dropout增强)和$\text{Fixed 0.1}$(两个样本使用相同的dropout)，性能会显著下降且结果相似。

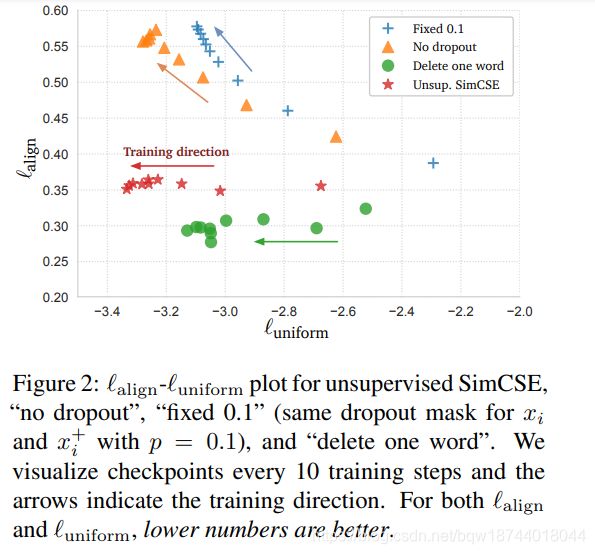
图2中，分别比较了$p=0$和$\text{Fixed 0.1}$两种极端情况，及删除一个单词方式的数据增强与$\text{SimCSE}$在alignment和uniformity上的表现。

• 可以发现所有的方法都能改善uniformity；
• 但是$p=0$和$\text{Fixed 0.1}$情况下的alignment会急剧下降，但是标准的$\text{SimCSE}$的alignment会非常的平稳；
• “删除一个单词”的方式能够改善alignment，但是在uniformity上的效果没有$\text{SimCSE}$好；

4. 其他实验设置的比较

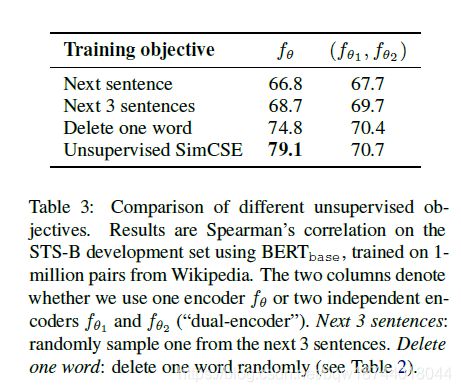
论文比较了$\text{next-sentence}$损失函数和对比损失函数，并比较了单个编码器和2个独立编码器的效果。实验结果如表3所示。

实验表明，对比损失函数显著优于$\text{next-sentences}$，且单个编码器显著优于2个独立的编码器

四、有监督SimCSE

有监督$\text{SimCSE}$主要的目标是利用有监督数据集来改善句嵌入向量表示。由于之前的研究已经证明了有监督自然语言推断(NLI)数据集对于学习句子嵌入向量非常有效。因此，在有监督$\text{SimCSE}$中我们同样使用$\text{NLI}$数据集来构造对比样本。

• $\text{NLI}$数据集中包含三种句子度关系，分别为：包含(entailment)、中立(neutral)、矛盾(contradiction)。

1. 探索有监督数据集

论文在各种句子对数据集上进行了实验，实验结果有：

• 所有的有监督句子对数据集都好于无监督的方法，也就是有监督是有效的；
• 在所有数据集中，使用$\text{NLI(SNLI+MNLI)}$数据集中的entailment构造正样本对效果最好；
• 初步分析认为$\text{NLI}$效果好的原因主要是，entailment样本对的词覆盖显著低于其他数据集；

2. 将contradiction样本对作为“难”负样本对

为了进一步利用$\text{NLI}$数据集，论文将contradiction样本对作为更加难的负样本对。

在$\text{NLI}$数据集中，通常会先给定一个前提(premise)，然后标注者需要写出三个句子，分别是：一个正确的句子(entailment)、一个可能正确的句子(neutral)和一个绝对错误的句子(contradiction)。因此，对于每个前提(premise)，都对应一个entailment句子和一个contradiction句子。

因此，在有监督$\text{SimCSE}$中，将$(x_i,x_i^{+})$扩展至$(x_i,x_i^{+},x_i^{-})$。其中，$x_i$是前提(premise)，$x_i^{+}$和$x_i^{-}$是entailment和contradiction。最终的训练目标${\ell }_i$定义为
$$-\text{log}\frac{e^{sim({\text{h}}_i,{\text{h}}_i^{+})/\tau }}{{\sum }_{j=1}^N(e^{sim({\text{h}}_i,{\text{h}}_j^{+})/\tau }+e^{sim({\text{h}}_i,{\text{h}}_j^{-})/\tau })}$$
实验结果表明，添加这样的“难”负样本对能够进一步改善模型效果，这也是我们最终的有监督$\text{SimCSE}$。

五、与Anisotropy的关系

1. 各向异性问题(anisotropy)

最近的研究表明语言模型的表示具有各向异性(anisotropy)的问题，例如：学习到的嵌入向量出现在向量空间中的一个狭窄圆锥中，这极大的限制了表达能力。Gao等人称这个问题为“表示退化”问题。此外，Wang等人的研究显示词嵌入矩阵的奇异值会急剧衰减。简单来说，除了少数奇异值外，其他奇异值都接近0。

2. 不同的解决方案

• 一种解决方案是：后处理，通过消除主成分、或者将表示空间映射至各向同性(isotropic)分别中。
• 另一种方案是，在训练过程中添加正则约束。

3. 证明对比学习能够解决各向异性问题

对比学习损失函数可以被近似为
$$-\frac{1}{\tau }{\mathbb{E}}_{(x,x^{+})\sim p_{pos}}[f(x{)}^{\top }f(x^{+})]+{\mathbb{E}}_{x\sim p_{data}}[log{\mathbb{E}}_{x^{-}\sim p_{data}}[e^{f(x{)}^{\top }f(x^{-})/\tau }]]\text{\hspace{1em}(1)}$$
其中，公式$(1)$的第一项用于保证正样本对的相似，而第二项则是将负样本对的距离拉开。

当$p_{data}$在有限样本集$\{x_i{\}}_{i=1}^m$上均匀分布且${\text{h}}_i=f(x_i)$，我们可以利用Jensen不等式来推断公式$(1)$中的第二项
$$\begin{array}{rl}& {\mathbb{E}}_{x\sim p_{data}}[log{\mathbb{E}}_{x^{-}\sim p_{data}}[e^{f(x{)}^{\top }f(x^{-})/\tau }]]\\ & =\frac{1}{m}\sum _{i=1}^{m}log\left(\frac{1}{m}\sum _{j=1}^m{e}^{{\text{h}}_i^{\top }{\text{h}}_j/\tau }\right)\\ & \ge \frac{1}{\tau m^2}\sum _{i=1}^m\sum _{j=1}^m{\text{h}}_i^{\top }{\text{h}}_j\end{array}$$
若令$\text{W}$表示样本集$\{x_i{\}}_{i=1}^m$的句嵌入矩阵($\text{W}$的第i行是${\text{h}}_i$)。那么最小化公式$(1)$的第二项，本质上等于由于${\text{WW}}^{\top }$中所有元素之和的上界，因为
$$\text{Sum}({\text{WW}}^{\top })=\sum _{i=1}^m\sum _{j=1}^m{\text{h}}_i^{\top }{\text{h}}_j$$
其中，${\text{h}}_i$是标准化的向量，因此${\text{WW}}^{\top }$的所有对角线元素均为1。

由于Gao等人发现${\text{WW}}^{\top }$在绝大多数情况下，所有的元素都是整数。那么根据Merikoski的结论可以得知$\text{Sum}({\text{WW}}^{\top })$是${\text{WW}}^{\top }$最大特征值的上界。

因此，可以推导出

• 最小化公式$(1)$的第二项等价于最小化$\frac{1}{\tau m^2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\text{h}}_i^{\top }{\text{h}}_j$的上界；
• 等价于最小化$\text{Sum}({\text{WW}}^{\top })$的上界；
• 等价于最小化${\text{WW}}^{\top }$的最大特征值上界；
• 也就是减小${\text{WW}}^{\top }$的最大特征值；

因此，对比损失函数本质上拉平了嵌入空间的奇异值，改善了uniformity。

六、实验

• 有/无监督$\text{SimCSE}$能够极大的改善句嵌入的效果(句向量相似度代码句语义相似性)；
• 虽然改善了句嵌入，但是句嵌入并不能改善下游的迁移任务；
• 使用$\text{[CLS]}$来表示句向量的效果最好；
• 将$\text{MLM}$作为辅助训练目标函数，可以改善模型在下游迁移任务上的效果；