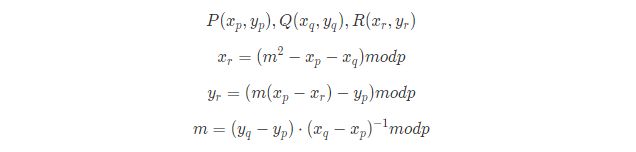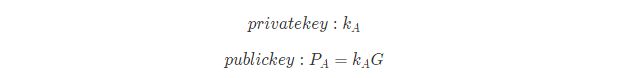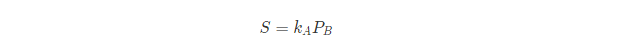java取模运算定律_简述椭圆曲线算法（ECC）

本文主要目的是对椭圆曲线做一个形象的介绍，比较通俗的可以理解与传统的基于取模运算的加密算法如RSA的区别。没有涉及过多密码学运算和数论知识。

如果感兴趣可以参考Elliptic Curve Cryptography: a gentle introduction，比较容易看懂，其中还配置了一个可视化的椭圆曲线工具，本文的配图都是利用该工具生成的。

好了，开始进入主题：Elliptic Curve Cryptography (ECC)

1. 简单概念

Elliptic Curve Cryptography 椭圆加密算法，简称ECC，是基于椭圆曲线数学理论的一种非对称加密算法(公钥加密算法),与RSA这些广为使用的加密算法相比，尽管目前ECC加密算法也应用的很广泛，当其基本的实现原理还是对大多数人来说比较陌生。

特性：与RSA相比可以使用更短的密钥实现与RSA相当或者更高的安全性。

一下方程式表示了椭圆曲线，其中a, b, c, d为系数。

y^2 = ax^3 + bx^2 + cx + d

当a = 1, b = 0, c = -7, d = 10 时，方程表示如下图所示：

y^2 = x^3 - 7x + 10

此时曲线显示如下图蓝线所示：

可以看出椭圆曲线并不是椭圆形的，形状与名称并没有太大联系。

2. 运算法则

2.1 加法

在这里我们取最简单的一种方式来解释椭圆曲线中的加法，其它的特殊方式可以参考 Elliptic Curve Cryptography: a gentle introduction

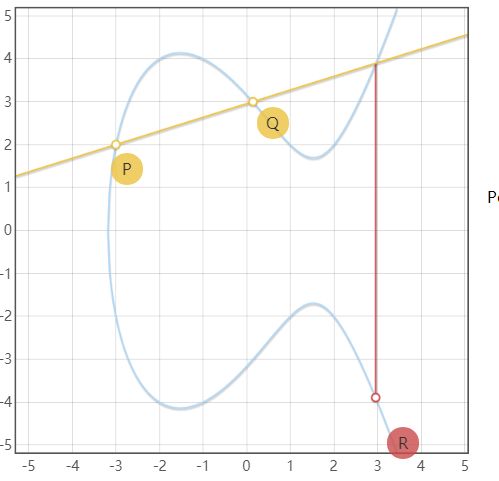
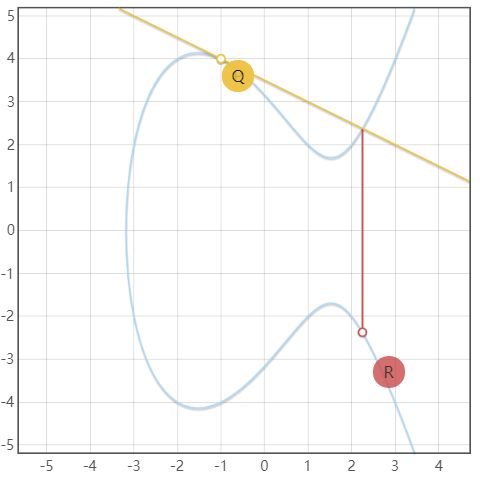
如下图所示，过曲线上两点P和Q画一条直线，与曲线交点关于x轴对称位置的点R，即为P + Q。 R = P + Q

2.2 二倍运算

当2.1中Q = P的时候，可以得到R = 2P。但此时无法用上述方法进行解释。因此在这种情况下，两点重叠的时候，将椭圆曲线在P点的切线，与椭圆曲线的交点关于x轴对称位置的点，定义为R，即2P。如下图所示：

2.3 无穷远点

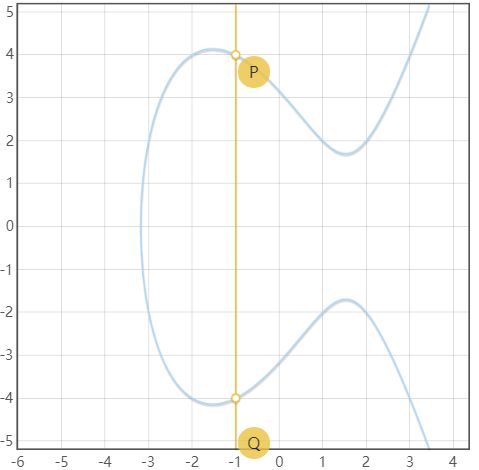
当Q = -P 的时候，此时两点所在直线与x轴垂直，此时不会与曲线有交点，此时定义P + Q = 0 ，其中0称之为无穷远点。

此种情况如下图所示：

综上，当给出椭圆曲线上一点G的时候，根据加法和二倍运算，可以求出2G、3G(拆分为G+2G)、... 、nG。

2.4 乘法

除了定义完加法和二倍运算，接下来定义乘法：

nG = G + G + ... + G

看成n个G相加。

如果按照上面方法应该进行n次加法，这样计算量较大。

另一种较为快速的方法就是先做倍数再做加法，如下面例子所示

151P = 2^7P + 2^4P +2^2P + 2^1P + 2^0P

可以先拿到P

在根据二倍运算获取2P

2P与P相加

2P取二倍运算得到4P

以此类推

这样只是做了简单的倍数运算和加法运算

但是当给出的是nG 和G 的时候如何求出n，是一个困难的问题，这也就是椭圆曲线加密背后的数学难题，详细过程可以参考Elliptic Curve Cryptography: finite fields and discrete logarithms。从一个方向上进行计算十分简单，当逆过来的时候却十分困难，这于大数分解和离散对数问题是一致的。

3. 有限域上的椭圆曲线

在我们上面描述的椭圆曲线中，可以从给出的示例图看出，对应的椭圆曲线都是光滑的曲线，这是基于实数域上的椭圆曲线。但是在实际上的椭圆曲线加密算法当中，用的不是实数域上的椭圆曲线，而是有限域上的椭圆曲线。

所谓有限域指的就是具有有限数量元素的集合，其中一个有限域的例子就是一个集合的整数模p，此时的p指的是一个素数，该有限与用GF(p)代表。

原本实数域上的椭圆曲线定义如下：

{ (x, y) \in(\mathbb{R_p})^2 | y^2 = x^3 + ax +b, 4a^3 +27b^2 \neq 0 } \bigcup {0}

(\mathbb{F_p})^2

有限域上的椭圆曲线定义如下：

{ (x, y) \in(\mathbb{F_p})^2 | y^2 \equiv x^3 + ax +b(mod p), 4a^3 +27b^2 !\equiv 0 (mod p)} \bigcup {0}

其中0代表无穷远点，a和b是

此时的椭圆曲线不再是一条光滑的曲线而是一个有限点集。

当a = 1, b = 1, p = 23的时候，此时有限域上的椭圆曲线如下图所示：

可以看到椭圆曲线不再是“曲线”，而是一堆点集。

此时有限域中的直线也不同于实数域中的实线。在有限域中直线定义为满足下面等式的点的集合。

ax + by + c \equiv 0(mod p)

4.有限域上的计算

在有限域上如何计算 xG：

在有限域GF(p)中给定椭圆曲线上两点P和Q，计算R = P + Q公式及过程如下：

P(x_p,y_p),Q(x_q,y_q), R(x_r,y_r)

x_r = (m^2 -x_p - x_q) mod p

y_r = (m(x_p - x_r)-y_p) mod p

m = (y_q - y_p) \cdot (x_q - x_p)^{-1} mod p

若 P = Q，则有：

m = (3x_p^2+a) \cdot (2y_p)^{-1} mod p

根据以上公式仍然可以跟实数域上一般计算出对应2G、3G、...、nG

5. 椭圆曲线使用原理

椭圆曲线加解密也是属于公钥加密体系的内容，也就是说需要跟RSA这种公钥加密算法一样有对应的公钥和私钥，那这里面的公钥和私钥又是如何得到的？

椭圆曲线加密中需要找到类似于RSA和DH类似的质因子分解或者离散对数求解的数学难题。在前面已经讲到给定椭圆曲线上一点G，那么求出nG是容易的，但是当拥有G和nG的时候计算出n却是困难的，这就是椭圆曲线上的离散对数问题。

先设私钥为k，可以计算出公钥为P = kG，其中G为曲线上一点

5.1 ECC加解密原理

5.1.1 加密选择随机数 r；

对消息进行加密 ( 所谓对消息进行加密即先对消息进行编码映射到曲线上的一点M，再对M进行计算 )，生成密文C，其中密文为一个点对

C = {rG, M + rP}

其中P为公钥

5.1.2 解密原理

先计算出M

M + rP - k(rG)

= M + r(kG) - k(rG) = M

- 再对M进行解密获取原始消息。

其中k 为私钥， P为公钥

### 5.2 ECC签名原理(ECDSA)

假设需要签名消息为M，M对应的hash值为h，一般签名都是对消息的hash值进行操作，而不是对消息本身。公钥加密速度慢，一旦消息过长，对消息本身签名会造成较大的计算和时间开销，一般采用对消息的hash进行签名。

#### 5.2.1 私钥签名

- 取随机数r，计算rG

- 根据r ， h， 私钥k，进行以下计算，其中x为G点横坐标

```math

s = (h + kx) / r生成签名S = {rG, s}

将M，签名S发送给接收方

5.2.2 公钥验签接收方收到消息M，签名S = {rG, s}

根据M计算hash值h

使用发送方公钥P计算hG / s + xP / s

将计算结果与rG进行比较，若相当则验证成功。

hG / s + xP /s

= hG / s + x(kG) / s

= (h + xk)G / s

= (h + xk)G r / (h + kx) = rG

可以注意到由于随机数的存在，所以对于同一条消息，用同一种算法，生成的签名都是不一样的。

5.3 椭圆曲线密钥交换( ECDH )

当通讯双方需要安全地交换信息且即使第三方拿到交换的信息也无法解码。

一般ECDH用来实现交换对称密钥。

流程如下，设通信双方是Alice和Bob

Alice 生成私钥和公钥：

private key : k_A

public key : P_A = k_AG

Bob 生成私钥和公钥：

private key : k_B

public key : P_B = k_BG

Alice和Bob通过非安全通道交换各自的公钥

Alice在收到Bob的公钥后，进行以下计算：

S = k_AP_B

Bob在收到Alice的公钥后，进行以下计算：

S = k_BP_A

可以看到Alice和Bob计算出来的密钥S是相同的，因为有：

S = k_AP_B = k_A(k_BG) = k_B(k_AG) = k_BP_A

此时通信双方拥有共享密钥，就可以通过对称加密来安全交换信息。

有时候会看到ECDHE，其中多出来的“E”主要指“Ephemeral”，即临时，短暂的意思，意味着交换的密钥是作为临时密钥，并非用来做长久密钥的，如TLS

5.4 比较

此处比较主要引自博客

5.4.1 密码强度比较对称密钥

ECC

RSA

80

163

1024

112

233

2240

128

283

3072

192

409

7680

拿表中第一行数据来举例，表示1024-bit的RSA密钥强度、163-bit的ECC密钥强度和80-bit的对称密钥强度相当。

即要达到相同的密钥强度所需要的的密钥长度： 对称 < ECC < RSA

5.4.1 计算性能比较

环境：Intel Xeon CPU E5520 @ 2.27GHz

基础：tommathlib

结果(单位us)：

算法

验证

签名

RSA-1024

12

511

RSA-2048

30

3270

ECDSA-192

590

490

可以看出对于ECDSA来说生成签名和验证签名开销差不多，对于RSA来说，验证签名比生成签名高效。

总的来说：

ECDSA生成签名性能比RSA好；

RSA验证签名性能比ECDSA好；

ECDSA签名算法适合用于签名和验证签名频率相近的场景，如P2P通道建立

RSA签名算法适用于，验证频率高，签名频率低的场景。