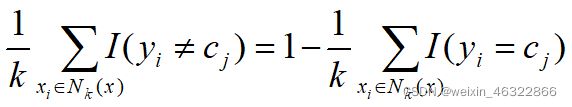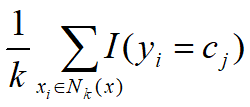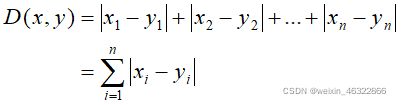数据挖掘经典算法（一）：K近邻（KNN）

目录

一、算法思想

二、算法原理

（1）KNN算法原理

（2）KNN算法三要素

① 分类决策规则

② K值的选择

③ 距离度量

（3）KNN实现方法

 ① 构建KD树

 ② KD树的搜索

 ③ KD树的分类（预测）

 （4）KNN算法之训练样本不平衡情况

 （5）算法优缺点

三、算法实验

 （1）数据收集与处理

 （2）实验及结果

---

一、算法思想

       在讲解K近邻算法之前，我们先通过一个很简单的例子进入主题。在我们日常生活中，我们会遇到很多决策。比如说，我会考虑换什么手机，或者中午吃什么。这个时候我给大家三个方案选择：

1、随便选一个

2、问问周围其他人的选择

3、做一份详细的报告，根据自身的情况量身定制选择方案

       相信大部分人都会选择第二个选项，如果选择选项1，意味着你会承担更高的风险，最后选择了一个非常不靠谱的选项。选择选项3你会发现会花费更多的计算成本在一个不是很重要的事件上。

       在我们选择下一台手机品牌时，我们就会先问其他人在用什么！当我们发现身边其他人，用安卓的大于用苹果的，这时我们下一台手机就会考虑安卓手机，这就是K近邻算法（KNN）。总结上面的例子KNN的思想可以总结为：近朱者赤，近墨者黑。

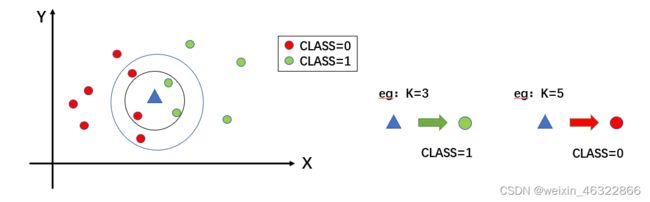
KNN分辨待测样本点类型的方法，如下图。

第一步：先找到待测样本周围最近的已知样本点。

第二步：统计周围已知样本点分布状况。

第三步：将待测样本类别归为优势方。

二、算法原理

（1）KNN算法原理

     KNN算法是选择与输入样本在特征空间内最近邻的k个训练样本并根据一定的决策规则，给出输出结果 。

决策规则：

    分类任务：输出结果为k各训练样本中占大多数的类。

    回归任务：输出结果为k个训练样本值的平均值。

（2）KNN算法三要素

 K值的选择、距离度量和分类决策规则是K近邻算法的三要素。

① 分类决策规则

KNN算法一般是用多数表决方法，即由输入实例的K个邻近的多数类决定输入实例的类。这种思想也是经验风险最小化的结果。

训练样本为(xi , yi)。当输入实例为 x，标记为c，是输入实例x的k近邻训练样本集。

我们定义训练误差率是K近邻训练样本标记与输入标记不一致的比例，误差率表示为：

 因此，要使误差率最小化即经验风险最小，就要使上式右端的

 最大，即K近邻的标记值尽可能的与输入标记一致，所以多数表决规则等价于经验风险最小化。

② K值的选择

       K取值较小时，模型复杂度高，训练误差会减小，泛化能力减弱；K取值较大时，模型复杂度低，训练误差会增大，泛化能力有一定的提高。

       KNN模型的复杂度可以通过对噪声的容忍度来理解，若模型对噪声很敏感，则模型的复杂度高；反之，模型的复杂度低。为了更好理解模型复杂度的含义，我们取一个极端，分析K=1和K=“样本数”的模型复杂度。

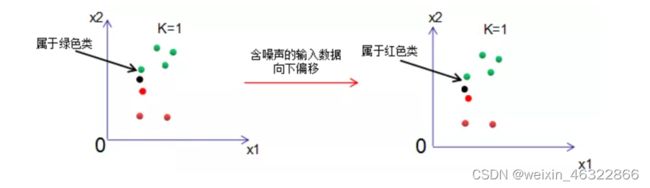
       K=1时，模型输出的结果受噪声的影响很大。

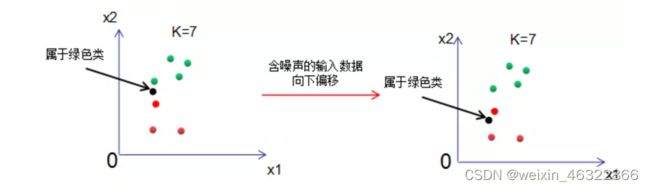
       由下图可知，样本数等于7，当K=7时，不管输入数据的噪声有多大，输出结果都是绿色类，模型对噪声极不敏感，但是模型太过简单，包含的信息太少，也是不可取的。

      通过上面两种极端的K选取结果可知，K值选择应适中，一般来说选择k的值是k = sqrt(N)，其中N代表训练数据集中的样本数，建议采用交叉验证的方法选取合适的K值。

③ 距离度量

KNN算法用距离来度量两个样本间的相似度，常用的距离表示方法：

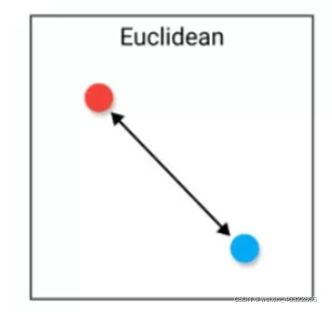
1、欧式距离

 2、曼哈顿距离

（3）KNN实现方法

       实现k近邻法时，主要考虑的问题是如何对训练数据进行快速K近邻搜索。这在特征空间的维数大及训练数据容量大时尤其必要。K近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很大时，计算非常耗时。为了提高KNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

       KD树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。KD树是是一种二叉树，表示对k维空间的一个划分，构造KD树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。KD树的每个结点对应于一个K维超矩形区域。利用KD树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

         KD树的KNN算法实现包括三部分：KD树的构建，KD树的搜索和KD树的分类。

 ① 构建KD树

        KD树实质是二叉树，其划分思想是切分使样本复杂度降低最多的特征。KD树认为特征方差越大，则该特征的复杂度亦越大，优先对该特征进行切分，切分点是所有实例在该特征的中位数。重复该切分步骤，直到切分后无样本则终止切分，终止时的样本为叶节点。

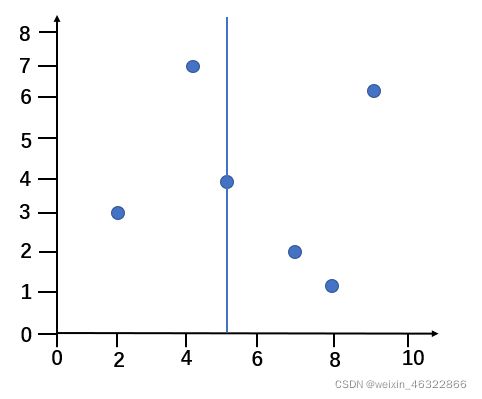
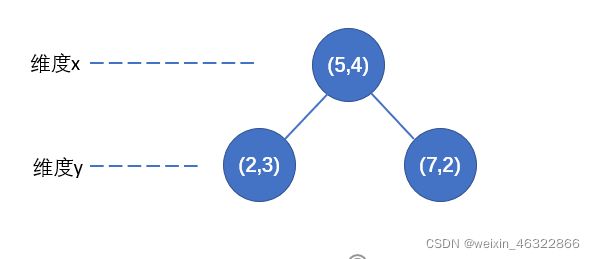
【例】给定一个二维空间的数据集：

 构造KD树的步骤：

1、数据集在维度X与Y上的方差分别为6.9和5.3， 因此首先从X的维度进行划分；

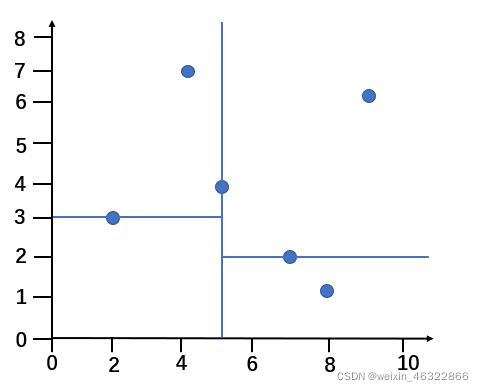
2、数据集在X维度的中位数是5，以平面X=5将空间分为左右两个矩阵；

3、分别对左右两个矩阵的样本在Y维度的中位数进行切分；

4、重复步骤2，3 ，直到无样本，该节点为叶子节点。

数据集在维度x与y上的方差分别为6.9和5.3，因此首先从x的维度进行划分;

       首先按x坐标排序，选中间值x=5做根节点，选出(5,4)，以平面x=5将空间分为左右两个矩形，所有x坐标比5小的都在左边，比5大的都在右边

 分别对左右两个矩形的样本在y维度的中位数进行切分;

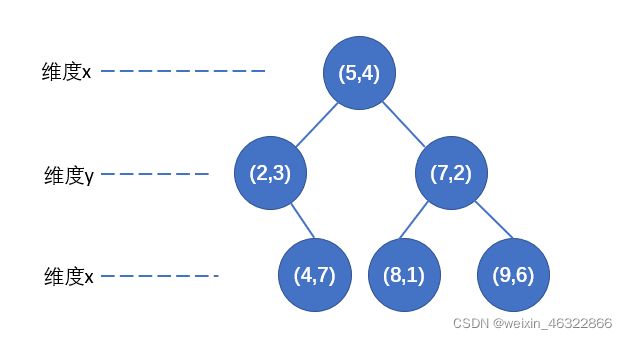
 重复上述两个步骤直到无样本，得到最后的KD树

 ② KD树的搜索

1、将查询数据Q从根结点开始，按照Q与各个结点的比较结果向下访问KD树，直至达到叶子结点。

        其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与m进行比较，若Q(k) < m，则访问左子树，否则访问右子树。达到叶子结点时，计算Q与叶子结点上保存的数据之间的距离，记录下最小距离对应的数据点，记为当前“最近邻点” 和最小距离。

（2）进行回溯操作，该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点，它们之间的距离小于最小距离。

       如果Q与其父结点下的未被访问过的分支之间的距离小于最小距离，则认为该分支中存在离Q更近的数据，进入该结点，进行（1）步骤一样的查找过程，如果找到更近的数据点，则更新为当前的“最近邻点” ，并更新最小距离。如果Q与其父结点下的未被访问过的分支之间的距离大于最小距离，则说明该分支内不存在与Q更近的点。回溯的判断过程是从下往上进行的，直到回溯到根结点时已经不存在与P更近的分支为止。

例如：查询点为(8.5, 6.5) ，比较到子节点(9, 6)：

       通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点(9,6)。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行‘回溯’操作。

 例如：查询点为(8.5, 6.5) ，回溯：

当前最近邻点： (9, 6) ， 最近邻距离： sqrt(0.5)

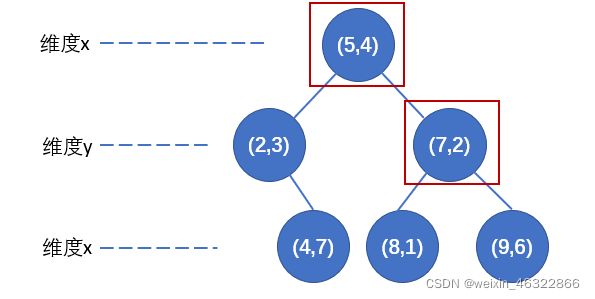
回溯：算法沿搜索路径反向查找是否有距离查询点更近的数据点。此例中先从(5,4)点开始进行二叉查找，然后到达(7,2)，最后到达(9,6)，此时搜索路径中的节点为大于(5,4)和(7,2)，小于(9,6)，首先以(9,6)作为当前最近邻点，计算其到查询点(8.5, 6.5)的距离为0.7071，然后回溯到其父节点(7,2)，并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以(8.5, 6.5)为圆心，以0.7071为半径画圆，发现该圆不和超平面y =2交割，因此不用进入(7,2)节点右子空间中去搜索。

再回溯到(5,4)，以(8.5, 6.5)为圆心，以0.7071为半径画圆更不会与x = 5超平面交割，因此不用进入(5,4)左子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点(9,6)，最近距离为0.7071。

③ KD树的分类（预测）

每一次搜寻与输入样本最近的样本节点，然后忽略该节点，重复同样步骤K次，找到与输入样本最近邻的K个样本 ，投票法确定输出结果。

当维数较大时，直接利用k-d树快速检索的性能急剧下降。假设数据集的维数为D，一般来说要求数据的规模N满足条件：N远大于2的D次方，才能达到高效的搜索。

（4）KNN算法之训练样本不平衡情况

若正负样本处于不平衡状态，运用投票决策的KNN算法判断输入样本的所属类别：

 结果显示输入样本为绿色类 。原因是红色类的个数远远小于绿色样本，导致出现的分类错误 。

解决方法：

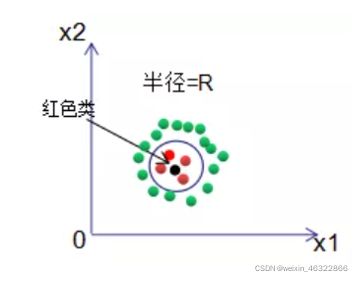
1、若分类决策选择限定半径最近邻法，即以输入样本为圆心，最大半径R的圆内选择出现次数最多的类做为输入样本的类 。如下图，黑色样本的分类结果正确。

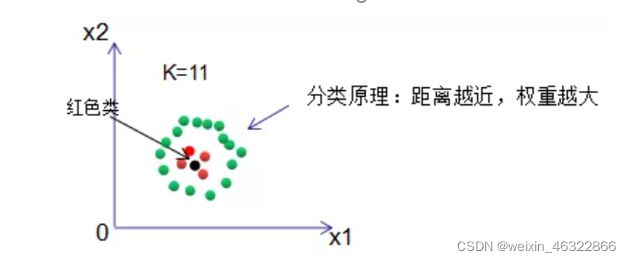
 2、投票法是默认每个样本的权重相等，我们假定权重与距离成反比，即距离越大，对结果的影响越小，那么该样本的权重也越小，反之，权重则越大，根据权重对输入样本进行分类。这种思想与AdaBoost算法相似，分类性能好的弱分类器给予一个大的权重 。

（5）算法优缺点

优点：

1）算法简单，理论成熟，可用于分类和回归。

2）对异常值不敏感。

3）可用于非线性分类。

4）比较适用于容量较大的训练数据，容量较小的训练数据则很容易出现误分类情况。

5）KNN算法原理是根据邻域的K个样本来确定输出类别，因此对于不同类的样本集有交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为合适。

缺点：

1）时间复杂度和空间复杂度高。

2）训练样本不平衡，对稀有类别的预测准确率低。

3）相比决策树模型，KNN模型可解释性不强。

三、算法实验

（1）数据收集与处理

利用爬虫工具，爬取了成都和桂林两地2020年的空气质量数据，经过数据处理分别对两地空气质量进行标签化，最终得到训练集与测试集。

 （2）实验及结果

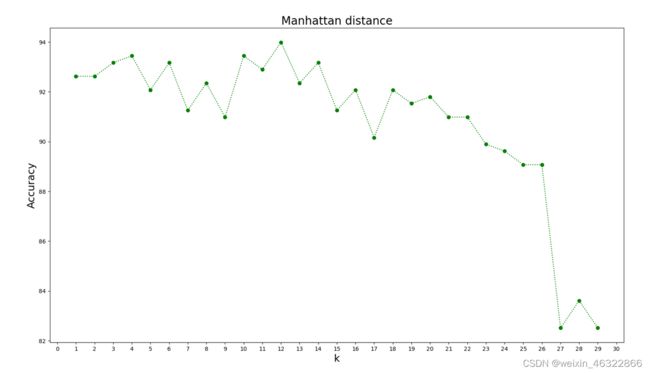
       我们取不同k值(1~30)使用Manhattan距离计算公式来预测测试集中空气质量，根据实验结果，当k=12时，得到的准确率最高；当k值大于20时，准确率会明显下降。

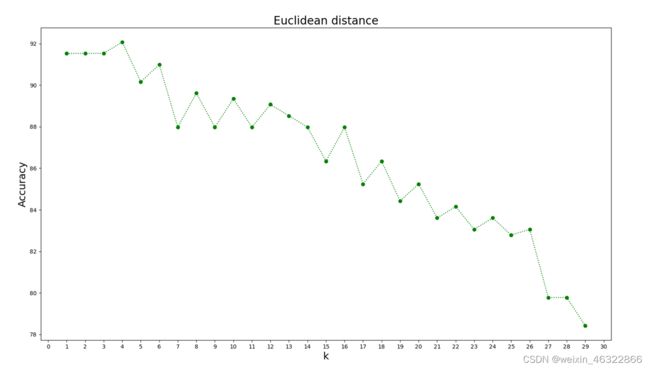
我们同样取不同k值(1~30)使用Euclidean 距离计算公式来预测测试集中空气质量，根据实验结果，当k=4时，得到的准确率最高；当k值大于16时，准确率会明显下降。

结论：k值的选取和距离计算方法对实验结果均有较大的影响，其中k值选取一般不能大于√样本数。