Python计算余弦相似度
余弦相似度常用在文本分类、图片分类等应用中,来计算两个文本或两个图像之间的相似度。
如下图,向量 a = [ x 1 , y 1 ] , b = [ x 2 , y 2 ] \boldsymbol a=[x_1,y_1],\boldsymbol b =[x_2,y_2] a=[x1,y1],b=[x2,y2]
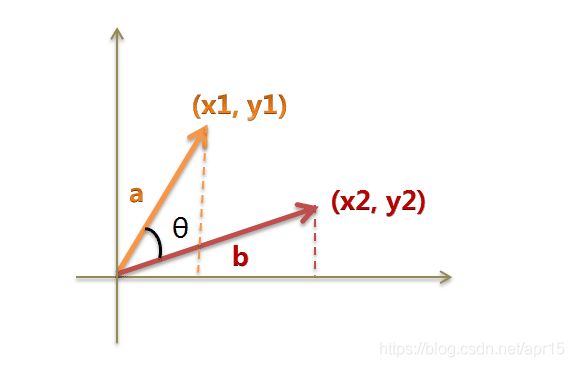 s i m ( a , b ) = c o s θ = a b ∣ a ∣ ∣ b ∣ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 sim(a,b) = cos \theta = \frac {ab}{\mid a \mid \mid b \mid} = \frac {x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}} sim(a,b)=cosθ=∣a∣∣b∣ab=x12+y12x22+y22x1x2+y1y2对于 n n n维向量 A = [ a 1 , a 2 , . . . a n ] , B = [ b 1 , b 2 , . . . b n ] A=[a_1,a_2,...a_n],B=[b_1,b_2,...b_n] A=[a1,a2,...an],B=[b1,b2,...bn],
s i m ( a , b ) = c o s θ = a b ∣ a ∣ ∣ b ∣ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 sim(a,b) = cos \theta = \frac {ab}{\mid a \mid \mid b \mid} = \frac {x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}} sim(a,b)=cosθ=∣a∣∣b∣ab=x12+y12x22+y22x1x2+y1y2对于 n n n维向量 A = [ a 1 , a 2 , . . . a n ] , B = [ b 1 , b 2 , . . . b n ] A=[a_1,a_2,...a_n],B=[b_1,b_2,...b_n] A=[a1,a2,...an],B=[b1,b2,...bn],
s i m ( A , B ) = A B ∣ A ∣ ∣ B ∣ = ∑ i = 1 n A i B i ∑ i = 1 n A i 2 ∑ i = 1 n A i 2 sim(A,B) = \frac {AB}{\mid A \mid \mid B \mid}= \frac {\sum_{i=1}^{n}{A_iB_i}}{\sqrt{\sum_{i=1}^{n}{A_i^2}}\sqrt{\sum_{i=1}^{n}{A_i^2}}} sim(A,B)=∣A∣∣B∣AB=∑i=1nAi2∑i=1nAi2∑i=1nAiBi
余弦相似度的取值范围在-1到1之间。余弦值越接近1,也就是两个向量越相似,完全相同时数值为1;相反反向时为-1;正交或不相关是为0。
求余弦相似度需要用到np.linalg.norm 操作,来求向量的范式,默认是L2范式,等同于求向量的欧式距离。
import numpy as np
t1 = np.array([-0.4,0.8,0.5,-0.2,0.3])
t2 = np.array([-0.5,0.4,-0.2,0.7,-0.1])
def cos_sim(a, b):
a_norm = np.linalg.norm(a)
b_norm = np.linalg.norm(b)
cos = np.dot(a,b)/(a_norm * b_norm)
return cos
print(cos_sim(t1,t2))
输出:0.23612240736068565