机器学习评估指标详细讲解，附python代码

听说点进蝈仔帖子的都喜欢点赞加关注~~
鸣谢：
https://zhuanlan.zhihu.com/p/36305931

分类指标

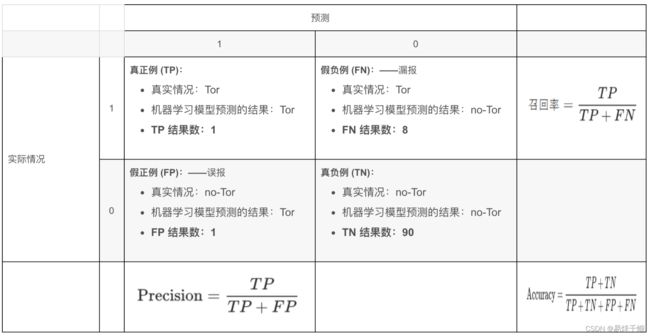
准确率通俗理解就是对于预测的所有数据，预测正确的数据占全部预测数据的比例。


以下符号均与上表一致。

import numpy as np
 
y_true = np.array([0, 1, 1, 0, 1, 0])
y_pred = np.array([1, 1, 1, 0, 0, 1])
 
#true positive
TP = np.sum(np.logical_and(np.equal(y_true,1),np.equal(y_pred,1)))
print(TP)
 
#false positive
FP = np.sum(np.logical_and(np.equal(y_true,0),np.equal(y_pred,1)))
print(FP)
 
#true negative
TN = np.sum(np.logical_and(np.equal(y_true,1),np.equal(y_pred,0)))
print(TN)
 
#false negative
FN = np.sum(np.logical_and(np.equal(y_true,0),np.equal(y_pred,0)))
print(FN)

准确率

准确率是最常用的分类性能指标。
Accuracy = (TP+TN)/(TP+FN+FP+TN)，即正确预测的正反例数 /总数

def get_classification_accuracy(feature_matrix, sentiment, coefficients):
    scores = np.dot(feature_matrix, coefficients)
    apply_threshold = np.vectorize(lambda x: 1. if x > 0  else -1.)
    predictions = apply_threshold(scores)
    
    num_correct = (predictions == sentiment).sum()
    accuracy = num_correct / len(feature_matrix)    
    return accuracy

精确率

精确率容易和准确率被混为一谈。其实，精确率只是针对预测正确的正样本而不是所有预测正确的样本。表现为预测出是正的里面有多少真正是正的。可理解为查准率。
Precision = TP/(TP+FP)，即正确预测的正例数 /预测正例总数
Precision 是分类器预测的正样本中预测正确的比例，取值范围为[0,1]，取值越大，模型预测能力越好。

from sklearn.metrics import precision_score, recall_score, f1_score
import numpy as np
 
y_true = np.array([[0, 1, 1],
                   [0, 1, 0]])
y_pred = np.array([[1, 1, 1],
                   [0, 0, 1]])
 
y_true = np.reshape(y_true, [-1])
y_pred = np.reshape(y_pred, [-1])
 
p = precision_score(y_true, y_pred, average='binary')
r = recall_score(y_true, y_pred, average='binary')
f1score = f1_score(y_true, y_pred, average='binary')
 
print(p)
print(r)
print(f1score)

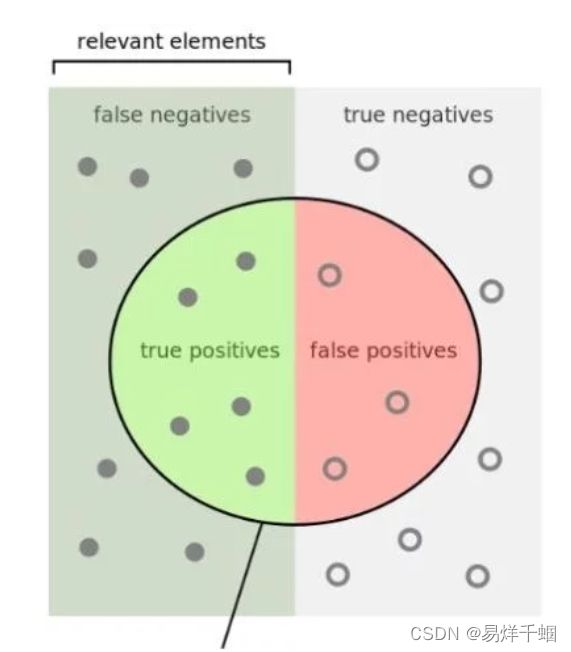
混淆矩阵 Confusion Matrix

这里牵扯到三个方面：真实值，预测值，预测值和真实值之间的关系，其中任意两个方面都可以确定第三个。

通常取预测值和真实值之间的关系、预测值对矩阵进行划分：

True positive (TP)
真实值为Positive，预测正确（预测值为Positive）
True negative (TN)
真实值为Negative，预测正确（预测值为Negative）
False positive (FP)
真实值为Negative，预测错误（预测值为Positive），第一类错误， Type I error。
False negative (FN)
真实值为Positive，预测错误（预测值为 Negative），第二类错误， Type II error。

召回率（查全率）Recall

Recall 是分类器所预测正确的正样本占所有正样本的比例，取值范围为[0,1]，取值越大，模型预测能力越好。

召回率与精确率的关系

ROC

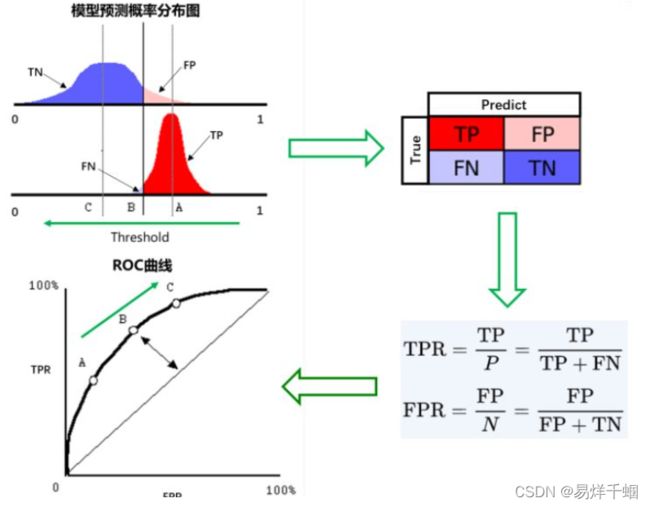
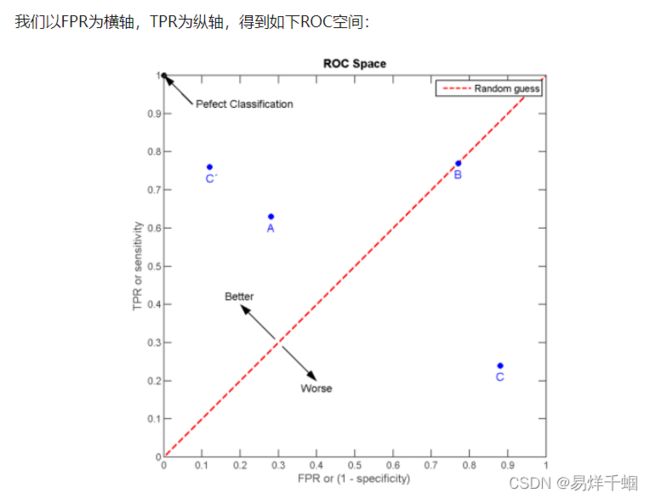
ROC曲线为 FPR 与 TPR 之间的关系曲线，这个组合以 FPR 对 TPR，即是以代价 (costs) 对收益 (benefits)，显然收益越高，代价越低，模型的性能就越好。

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc  ###计算roc和auc
from sklearn import cross_validation
 
# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
 
##变为2分类
X, y = X[y != 2], y[y != 2]
 
# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
 
# shuffle and split training and test sets
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=.3,random_state=0)
 
# Learn to predict each class against the other
svm = svm.SVC(kernel='linear', probability=True,random_state=random_state)
 
###通过decision_function()计算得到的y_score的值，用在roc_curve()函数中
y_score = svm.fit(X_train, y_train).decision_function(X_test)
 
# Compute ROC curve and ROC area for each class
fpr,tpr,threshold = roc_curve(y_test, y_score) ###计算真正率和假正率
roc_auc = auc(fpr,tpr) ###计算auc的值
 
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

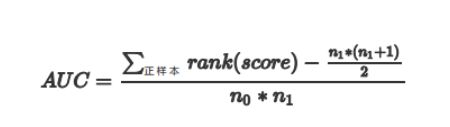
AUC

AUC定义：

AUC 值为 ROC 曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。
AUC = 1，是完美分类器。
0.5 < AUC < 1，优于随机猜测。有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。
注：对于AUC小于 0.5 的模型，我们可以考虑取反（模型预测为positive，那我们就取negtive），这样就可以保证模型的性能不可能比随机猜测差。

def acu_curve(y,prob):
    fpr,tpr,threshold = roc_curve(y,prob) ###计算真正率和假正率
    roc_auc = auc(fpr,tpr) ###计算auc的值
 
    plt.figure()
    lw = 2
    plt.figure(figsize=(10,10))
    plt.plot(fpr, tpr, color='darkorange',
             lw=lw, label='ROC curve (area = %0.3f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
    plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Receiver operating characteristic example')
    plt.legend(loc="lower right")
 
    plt.show()

拟合（回归）

是否预测了正确的数值

为了应对这种状况，sklearn中使用RSS的变体，均方误差MSE（mean squared error）来衡量我们的预测值和真实值的差异。均方误差，本质是在RSS的基础上除以了样本总量，得到了每个样本量上的平均误差。有了平均误差，我们就可以将平均误差和我们的标签的取值范围在一起比较，以此获得一个较为可靠的评估依据。
在sklearn当中，我们有两种方式调用这个评估指标，一种是使用sklearn专用的模型评估模块metrics里的类mean_squared_error，另一种是调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差。cross_val_score的均方误差为负。我们在决策树和随机森林中都提到过，虽然均方误差永远为正，但是sklearn中的参数scoring下，均方误差作为评判标准时，却是计算”负均方误差“（neg_mean_squared_error）。这是因为sklearn在计算模型评估指标的时候，会考虑指标本身的性质，均方误差本身是一种误差，所以被sklearn划分为模型的一种损失(loss)。在sklearn当中，所有的损失都使用负数表示，因此均方误差也被显示为负数了。真正的均方误差MSE的数值，其实就是neg_mean_squared_error去掉负号的数字。

除了MSE，我们还有与MSE类似的MAE（Mean absolute error，绝对均值误差）。其表达的概念与均方误差完全一致，不过在真实标签和预测值之间的差异外我们使用的是L1范式（绝对值）。现实使用中，MSE和MAE选一个来使用就好了。
在sklearn当中，我们使用命令from sklearn.metrics import mean_absolute_error来调用MAE，同时，我们也可以使用交叉验证中的scoring = “neg_mean_absolute_error”，以此在交叉验证时调用MAE。
RSS残差平方和
MSE:均方误差
RMSE:均方根误差
MAE:平均绝对误差

平均绝对误差 MAE
MAE:Mean Absolute Error）平均绝对误差，从图形上看，MAE 就相当于将数据点与拟合之间之间的距离绝对值之和。

from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression
# 已定义X,y
classifier = LinerRegression()
classifier.fit(X, y)

guesses = classifier.predict(X)

error = mean_absolute_error(y, guesses)

均方误差 MSE

MSE:（Mean Squared Error）均方误差，从图形上看，为数据点到拟合直线之间的距离的平方。

from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
# 已定义X,y
classifier = LinearRegression()
classifier.fit(X,y)

guesses = classifier.predict(X)

error = mean_squared_error(y,guesses)

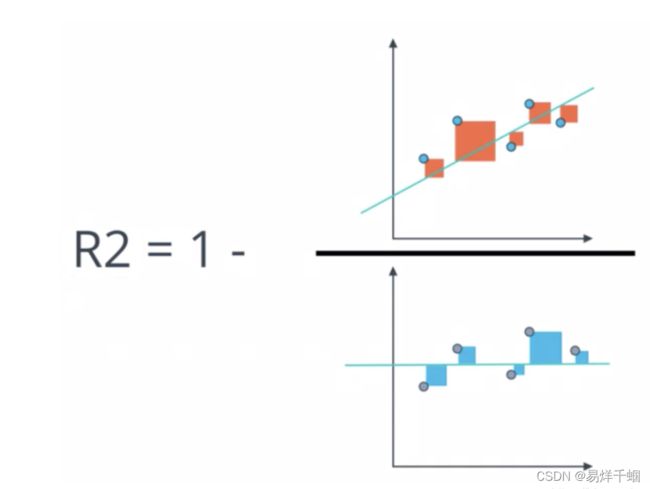
是否拟合到了足够的信息

以上描述的都是评价标准的第一个角度，即：是否预测到了正确的数值。
对于回归类算法而言，只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外，我们还希望我们的模型能够捕捉到数据的”规律“，比如数据的分布规律，单调性等等，而是否捕获了这些信息并无法使用MSE来衡量。比如，对数据进行回归，前端大部分预测的效果很好，但是后面部分的预测结果并不好，这样使用第一种角度考虑预测的结果，其实效果还很好，但是拟合的函数并没有准确的学习到数据的分布和走势。

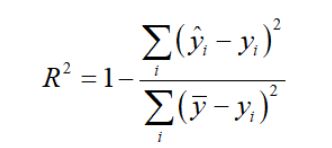
也可以套娃计算得到。

from sklearn.metrics import r2_score

y_true = [1, 2, 4]
y_pred = [1.3, 2.5, 3.7]

r2_score(y_true, y_pred)

解决评估指标鲁棒性问题

我们通常用一下两种方法解决评估指标的鲁棒性问题：

剔除异常值
设定一个相对误差 ，当该值超过一定的阈值时，则认为其是一个异常点，剔除这个异常点，将异常点剔除之 后。再计算平均误差来对模型进行评价。
使用误差的分位数来代替
如利用中位数来代替平均数。例如 MAPE:

MAPE是一个相对误差的中位数，当然也可以使用别的分位数。