图神经网络(CS224w)学习笔记3 Node Embeddings
文章目录
- 章节前言
-
- 为什么要Embedding?
- Embedding的例子
- 本章主要内容
- 一、Node Embeddings: Encoder and Decoder
-
- 1.1 编码器
-
- 1.1.1 “浅”编码 “shallow” encoding:
- 1.2.2 Encoder + Decoder Framework Summary
- 1.3 节点相似的不同定义
- 1.4 Note on Node Embeddings
- 二、Random Walk Approaches for Node Embeddings
-
- 2.1 统一符号表示
- 2.2 随机游走:
-
- 2.2.1 random walk embeddings
- 2.2.2 random walks优点
- 2.3 无监督特征学习
- 2.4 Feature Learning as Optimization
- 2.5 随机游走优化过程:
- 2.6 随机游走算法的总结:
- 2.7 如何执行随机游走
- 2.8 node2vec概述
- 2.9 有偏游走:
-
- 2.9.1 随机游走算法步骤:
- 2.9.2 其他随机游走方法
- 2.10 Summary so far
- 三、Embedding Entire Graphs
-
- 3.1 方式一
- 3.2 方式二
- 3.3 方式三 匿名随机游走(Anonymous walk embeddings)
-
- 3.3.2 New idea:learn walk embeddings
- 3.4 总结
章节前言
首先对上节课所讲的针对于图的传统机器学习进行回顾。关于此内容,上个学习笔记已经记载很多了(不清楚地可以点链接),在此不再叙述。

为什么要Embedding?
Embedding的例子
本章主要内容
本章主要讲了如何使用节点嵌入:聚类、社区发现,节点分类,链接预测(通过concatenate、哈达玛积、取平均、求和、计算距离来得到链接嵌入),图分类(聚合节点嵌入或使用匿名随机游走获得图嵌入)
一、Node Embeddings: Encoder and Decoder
假设我们有一个图G,其中V是顶点集,A是邻接矩阵。
为简单起见:没有使用节点特性或额外信息。

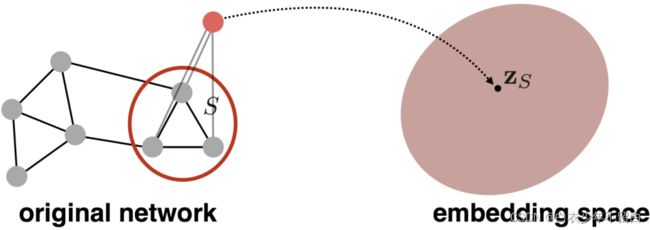
目标是对节点进行编码,使嵌入空间的相似性(例如,点积)近似于图中的相似性。

编码器从节点映射到嵌入:定义一个节点相似函数(即,原始网络中相似度的度量)
Decoder DEC 将embedding对映射为相似度得分
优化编码器参数,使:

1.1 编码器
将每个节点映射到低维向量,这里的d一般是64-1000维。

最简单的编码方法:Encoder只是一个嵌入式查找。

1.1.1 “浅”编码 “shallow” encoding:

上图中,映射矩阵Z每列是一个节点所对应的embedding向量。v是一个其他元素都为0,对应节点位置的元素为1的向量。通过矩阵乘法的方式得到结果。
这种方式就是将每个节点直接映射为一个embedding向量,我们的学习任务就是直接优化这些embedding。
缺点:参数多,很难scale up3到大型图上。
优点:如果获得了Z,各节点就能很快得到embedding。
有很多种方法:如DeepWalk,node2vec等
1.2.2 Encoder + Decoder Framework Summary
- 浅层编码器:嵌入查找
- 优化参数:包含节点嵌入 _ zu对于所有节点∈
- 我们将在第6讲中介绍深层编码器(gnn)
- 解码器:基于节点相似度
- 目的:对相似的节点对(,)最大化 T _^Τ_ zvTzu
1.3 节点相似的不同定义
- 有边
- 共享邻居
- 有相似的structural roles
本节课将学习:随机游走(random walk)定义的节点相似度以及如何为这样的相似性度量优化嵌入
1.4 Note on Node Embeddings
这是学习节点嵌入的无监督/自我监督方式。
- 我们不使用节点标签
- 我们没有利用节点特性
- 目标是直接估计节点的一组坐标(即嵌入),以便保留网络结构的某些方面(由DEC捕获)。
这些嵌入是独立于任务的,因为它们不是为特定的任务而训练的,但可以用于任何任务。
二、Random Walk Approaches for Node Embeddings
2.1 统一符号表示
向量 z u ⃗ \vec{z_u} zu:节点的嵌入(我们的目标)
概率函数 P ( v ∣ z u ⃗ ) P(v|\vec{z_u}) P(v∣zu):从节点开始随机遍历访问节点的(预测)概率。
下面两个分线性函数被用来生成预测概率:

Softmax函数:将K个实值组成的向量变成一个和为1的由K个概率组成的概率向量。
Sigmoid函数:是一个S形状的函数,能够将实值映射成(0,1)区间的值。
2.2 随机游走:
给定一个图 G G G和一个开始节点 v v v,我们随机挑选这个节点的邻居节点 v u i v_{u_i} vui,然后移到这个邻居节点 v u i v_{u_i} vui,以这个邻居节点作为开始点重复这个过程。到达一定次数之后这个过程结束。在整个过程中访问的节点序列就是图上的随机游走。如下图所示:

2.2.1 random walk embeddings
随机游走嵌入: z u T z v \mathbf{z}_{u}^{\mathrm{T}}\mathbf{z}_v zuTzv表示u和v同时出现在图的随机游走过程的概率。
随机游走Embedding的执行步骤:
- 用随机游动策略R估计从节点u开始的随机游走中访问节点v的概率。

- 优化这些embedding来编码随机游走统计参数。用embedding空间中的相似性(这个相似性需要专门的二元函数来计算,如简单的内积cos())来编码节点经过随机游走算法得出来的”相似性“。
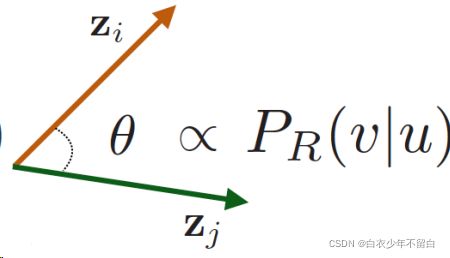
2.2.2 random walks优点
-
表达性强。灵活且随机的节点相似性定义能够整合节点局部和全局的邻居信息。
思想:如果从节点u开始的随机游走过程以高概率访问到节点v,那么节点u 和节点u有“很强的关系“,他们是相似的。 -
高效:在训练过程中不需要考虑所有的节点对,仅仅需要考虑在随机游走过程中出现的节点对。
2.3 无监督特征学习
- 目的:在d维空间中,找到能够保存图节点相似性的节点嵌入。
- 思路:在embedding空间中临近的节点在网络中连接的紧密。
- 给定一个节点u,如何定义节点中连接紧密的节点?
N R ( u ) N_R\left( u \right) NR(u)表示以随机游走策略R取得的节点u的邻居。
2.4 Feature Learning as Optimization
目标是使对每个节点 u u u, N R ( u ) N_R(u) NR(u)的节点和 z ⃗ u \vec{z}_u zu靠近。即 P ( N R ( u ) ∣ z ⃗ u ) P(N_R(u)|\vec{z}_u) P(NR(u)∣zu)值最大。
f : u f:u f:u → R d \mathbb{R}^d Rd : f ( u ) = z ⃗ u f(u)=\vec{z}_u f(u)=zu
Log-likelihood 目标:

对这个目标函数的理解是:对节点 u u u,我们希望其表示向量对其random walk neighborhood N R ( u ) N_R( u ) NR(u) 的节点是predictive的(可以预测到它们的出现)
2.5 随机游走优化过程:
大致思路:
用随机游走策略 R R R以节点 u u u作为起始点执行一个短的且固定长度的随机游走过程。
N R ( u ) N_R\left(u\right) NR(u)表示 u u u的随意游走访问的节点集; N R ( u ) N_R\left( u \right) NR(u) 是一个多重集(multiset),即存在重复值。这符合随机游走过程的,因此很可能对某一个节点访问多次。
优化embedding是通过对给定的节点 u u u预测他的随机游走邻居 N R ( u ) N_R\left( u \right) NR(u)来实现。

等价于

这里上式变成下式仅仅是将集合 写成单个元素点的形式。
Intuition: 优化嵌入 z u z_u zu来最大化似然co-occurrences随机游走。
使用softmax函数来参数化 P ( v ∣ z ⃗ u ) P(v|\vec{z}_u) P(v∣zu),目的是我们希望节点v是所有N个节点中与节点u最相近的,而 ∑ i e x p ( x i ) ≈ max e x p ( x i ) ) \sum_iexp(x_i)\approx \max exp(x_i)) ∑iexp(xi)≈maxexp(xi))即与节点u最相近的占主导。
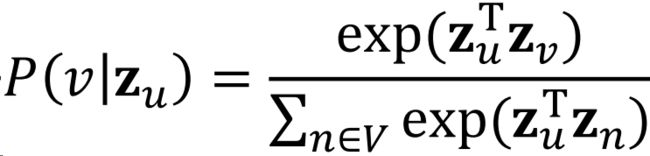
将 P ( v ∣ z ⃗ u ) P(v|\vec{z}_u) P(v∣zu)代入L得:

优化random walk embeddings就是找到embedding z \mathbf{z} z使L最小化

但是计算这个公式代价很大,因为需要内外加总2次所有节点,复杂度达 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2):
我们发现问题就在于用于softmax归一化的这个分母:

为了解决这个分母,我们使用negative sampling的方法:简单来说就是原本我们是用所有节点作为归一化的负样本,现在我们只抽出一部分节点作为负样本,通过公式近似减少计算。

这个随机分布不是uniform random,而是random in a biased way:概率与其度数成比例。
负样本个数k的考虑因素:
- 更高的k会使估计结果更鲁棒robust
- 更高的k会使负样本上的偏差bias更高
- 实践上的k常用值:5-20
在取得目标函数之后采用梯度或随机梯度下降法来解优化函数。梯度下降是使用所有样本来计算梯度,计算时间长,计算量大。随机梯度下降是使用一个样本来计算梯度,时间消耗短,但是梯度计算的随机性大;一般采样mini-batch梯度下降,即梯度和随机梯度的一个折中,主要思想是从样本中抽样一定数量样本进行梯度计算。此外梯度下降使用反向传播算法来更新参数值。
2.6 随机游走算法的总结:
- 对图中每一个节点都执行一次short fix-length 随机游走。
- 经过随机游走计算每个节点的随机游走邻居多重集合 N R ( u ) N_R\left( u \right) NR(u), N R ( u ) N_R\left( u \right) NR(u)存放的是从节点 开始经过随机游走算法得到的重复样点集。
- 用随机梯度下降法优化embedding(使用负样本来简化计算)

2.7 如何执行随机游走
到目前为止,我们讨论了对于给定的随机游走策略,如何优化所需的embedding.但是并没有说明如何执行随机游走算法!最简单的想法:对每一个节点执行定长,无偏随机游走,即DeepWalk from Perozzi et al., 2013,但是这种执行方式好像不太好,有局限性。这有个扩展Perozzi et al. 2014。
2.8 node2vec概述
- 目标:相似的网络邻居经过节点嵌入之后他们在特征空间的坐标也是临近的。
- 我们将这个目标建模为最大似然优化问题,且与后续的预测任务相互独立。
- Key observation: 如果节点有灵活的网络邻域概念 N R ( u ) N_R(u) NR(u),那么将会对更加丰富的节点嵌入。
- 开发2阶有偏随机游走策略 来生成节点 u u u的网络邻域. N R ( u ) N_R(u) NR(u)。参考Grover et al. 2016。
2.9 有偏游走:
思路:使用灵活、有偏能够平衡网络中的局部和全局概念。
下面说明两个经典的定义节点 u u u的网络邻域 N R ( u ) N_R\left( u \right) NR(u)的算法,即广度优先搜索和深度优先搜索:

两种方法的特点:
- BFS:关注节点邻居的微观结构
- DFS:关注节点邻居的宏观结构

下面介绍对于BFS和DFS两个重要的参数: - return parameter p p p :返回上一个节点的概率
- in-out parameter q q q:向外走(DFS)VS向内走(BFS)相比于DFS,选择BFS的概率
参数应用:使用有偏的2阶随机游走研究网络邻居。如下图
随机游走在边 ( S 1 , W ) \left( S_1,W \right) (S1,W)上穿梭,现在从 S 1 S_1 S1回到 W W W
从内部看, W W W的邻居节点只能是 S 1 , S 2 , S 3 S_1, S_2, S_3 S1,S2,S3, 且 W W W到 S 1 , S 2 S_1, S_2 S1,S2,的距离相等,到 S 3 S_3 S3的距离远于 S 1 S_1 S1。

Key idea: 记住游走过程的上一个节点。
随机游走在 ( S 1 , W ) \left( S_1,W \right) (S1,W)上游荡,现在在W节点处,下一步怎么走?(其中p,q是前面提到的模型转换概率)答:使用BFS和DFS算法

BFS和DFS算法在随机游走的性质是什么?参数 p , q p,q p,q应该怎么选择?
- BFS选择较小的 . 我的理解是因此BFS在随机游走中主要关注邻居的微观结构,不偏向于走的太远,所以更可能走重复的路径。
- DFS选择较小的. 我的理解是因为DFS在随机游走中主要关注邻居的宏观结构,希望走的很深,很远,所以要避免走重复的路径,尽可能去距出发节点较远的点。
2.9.1 随机游走算法步骤:
- 计算随机游走的两个概率参数 p , q p,q p,q。
- 对每一个节点模拟 r r r次长度为 l l l随机游走。
- 用随机梯度下降法优化ndoe2vec目标函数。
上述算法的特点:
- 线性时间复杂度。
- 所有的3个步骤都可以独立并行计算。
2.9.2 其他随机游走方法
2.10 Summary so far
- 节点嵌入:使embedding的向量距离能够反应原网络中的节点相似度。
- 衡量节点相似度的指标
2.1Naïve:连接两个节点时类似
2.2邻域重叠(在第2讲中已涉及)
2.3随机漫步方法(今天讨论) - 需要根据具体情况来选择算法。Node2vec在节点分类方面表现较好,而其他方法在链路预测方面表现较好 (Goyal and Ferrara, 2017 survey)。random walk approaches整体上更有效。一般来说:必须选择与应用程序匹配的节点相似度定义。
三、Embedding Entire Graphs
任务目标:嵌入子图或整个图 G G G,得到表示向量 z G \mathbf{z}_G zG 。
 任务:
任务:
- 分类有毒和无毒的分子
- 识别异常图。
也可以视为对节点的一个子集的嵌入。
3.1 方式一
最简单(但有效)的方法:使用上面的节点嵌入方式得到所有的节点嵌入;然后对所有的节点嵌入求合或者求平均(被Duvenaud et al., 2016用来做分子分类):

3.2 方式二
引入一个虚拟节点然后执行一个标准的图节点嵌入,将求得的虚拟节点嵌入作为整个图的嵌入(Li et al., 2016提出的一种通用的子图嵌入技术)。
3.3 方式三 匿名随机游走(Anonymous walk embeddings)
来自于Anonymous Walk Embeddings, ICML 2018
匿名游走中的状态对应于我们在随机漫步中第一次访问该节点的索引。

这种做法会使具体哪些节点被游走到这件事不可知(因此匿名)

note:Random walk2表示了同样的匿名随机游走结果。
匿名随机游走的个数随walk长度指数级增长:


匿名游走的简单使用:
- 设置随机游走的路径长度为l=3 。
- 按照上面的图表得到,随机游走的内容最多为5,因此我们可以都得一个5维的向量。
- Z G [ i ] \boldsymbol{Z}_G[i] ZG[i]表示 w i w_i wi在整个匿名游走的过程出现的概率。
随机游走的采样 - 抽样匿名游走:独立的生成集合数量为m 的随机walks。
- 将图表示成这个集合上的概率分布。
那就存在一个关键问题:我们应该采样多少次,即随机游走数量m 应该为多少?

3.3.2 New idea:learn walk embeddings
不同于简单的将游走发生的次数作为不同游走的表示,这节学习匿名游走 w i w_i wi的嵌入 z i z_i zi。
学习图嵌入 Z G Z_G ZG的同时学习所有匿名游走的嵌入 z i z_i zi , Z = { z i : i = 1... η } Z=\left\{ z_i:i=1...\eta \right\} Z={zi:i=1...η},其中 η \eta η表示采样随机游走的个数。
根据Anonymous Walk Embeddings, ICML 2018提供的思路,要想要嵌入walks要解决预测walks的任务,即给出一定数量某个节点的walks,然后利用这些walks预测下一步的walk。
步骤如下:
-
以节点u 原点执行T次长度为l 的随机游走得到 N R ( u ) = { w 1 u , w 2 u . . . w T u } N_R(u)=\left\{ w_{1}^{u},w_{2}^{u}...w_{T}^{u} \right\} NR(u)={w1u,w2u...wTu}。

-
利用采样得到的采样点,预测在 Δ s i z e \varDelta size Δsize窗口内发生的walks(例如,给定 w 1 , w 3 , Δ s i z e = 1 w_1, w_3, \varDelta size=1 w1,w3,Δsize=1预测 w 2 w_2 w2)
-
估计匿名游走 w i w_i wi的嵌入 z i z_i zi, η \eta η是所有可能的游走嵌入数目。

这里面有些部分我也是似懂非懂的,等我细细看完论文后,再回来补一下吧。
3.4 总结
我们讨论了图嵌入的3个概念:
- 方法1:嵌入节点并对其求和/取平均值
- 方法2:创建跨(子)图的超级节点,然后嵌入该节点
- 方法3:匿名随机游走嵌入
Idea 1:对匿名游走进行抽样,并用每一次匿名游走发生的次数的比例表示这个图。
Idea 2:嵌入匿名行走,连接它们的嵌入得到一个图嵌入