Functional Mechanism: Regression Analysis under Differential Privacy

Functional Mechanism: Regression Analysis under Differential Privacy

1. 摘要

差分隐私是一种能在保护隐私的同时发布敏感数据的方法。

目前，已经提出了很多种方法将差分隐私应用到回归分析中。但是，这些方法要么只能在某些非标准类型的回归中使用，

要么就无法达到足够的精度。

于是，为了解决上面的两个问题，作者提出了函数机制，并将它应用到了线性回归和 logistic 回归上。

那么函数机制有什么特别之处呢？现有的方法都是直接扰动最终的结果，而函数机制是在目标函数上进行扰动。

2. 介绍

2.1 函数机制的设计难点

1. 扰动目标函数比扰动标量要论难的多
2. 直接在目标函数的系数上加人噪声很容易导致注入了过量的噪声，从而导致函数无法收敛
3. 部分目标函数被扰动后可能失效，比如产生了无界的结果，或者多个局部最优。

2.2 函数机制的优点

• 对于线性回归和 logistic 回归，无论训练集的规模是多少，加入的噪声量是恒定的。
• 在 $ϵ$ - differential privacy上就能实现，不需要使用松弛化项 $\delta$

3. 准备工作

3.1 线性回归

线性回归假设目标值和特征之间线性相关，即可以通过多个特征来预测目标值。线性回归可以由以下公式表示：
$$y=\omega x+b（线性回归的一般表示）$$
其中，$\omega$ 是权重，b是偏移量。

线性回归的一个经典例子就是房价预测，使用占地面积，地段，房龄等特征来预测房价

线性回归使用均方误差来做损失函数，用梯度下降法来不断修正参数，使得预测结果变得越来越精确。

线性回归损失函数为 $L(\omega ,b)=\frac{1}{n}{\sum }_{i=1}^n(\omega x_i+b-y_i{)}^2$

线性回归的核心思路就是通过梯度下降求解损失函数最小时的 ${\omega }^{\ast }和b^{\ast }$
$$({\omega }^{\ast },b^{\ast })=argmin(\omega ,b)\sum _{i=1}^n(\omega x_i+b-y_i{)}^2$$

3.2 Logistic 回归

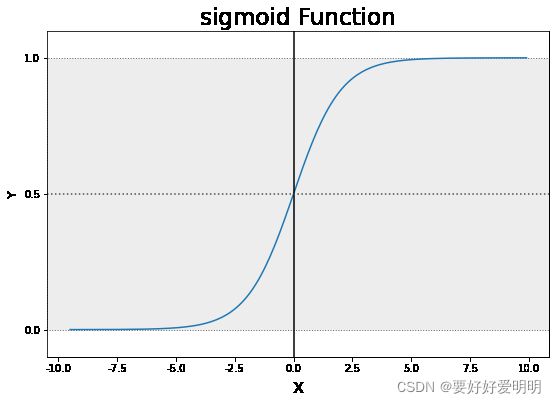
Logistic 回归常用于分类问题。它使用sigmoid函数将原函数转化成一个值在 $(0,1)$ 之间的分布。例如，我们可以将预测值大于 $0.5$ 的个体分为一类，小于等于 $0.5$ 的个体分为第二类。Logistic 的一般公式为：$y=\frac{e^{\omega x}}{1+e^{\omega x}}$

和线性回归不同的是，Logistic 回归的损失函数为对数损失函数。公式表示如下：
$$L(\omega ,b)=-[ylogy+(1-y)log(1-y)]$$
该损失函数可用分段函数表示为
$$L(\omega ,b)=\{\begin{array}{c}-log(y)y=1\\ -log(1-y)y=0\end{array}$$

Logistic 回归通过最小化损失函数来实现更精准的分类。

3.3 $ϵ$- Differential Privacy

差分隐私使查询随机化，让攻击者无法判断某条记录是否在数据集中。

如果一个随机化算法 $\mathcal{A}$ 满足 $\epsilon $- Differential Privacy，那么 $A$ 在任意两个相邻数据集 $D1$ 和 $D2$ 上的输出满足：
$$Pr[\mathcal{A}(D_1)=O]\le e^{ϵ}\cdot Pr[\mathcal{A}(D_2)=O]$$
其中 $O$ 表示输出的结果 ，$Pr$ 表示概率。

$ϵ$为隐私保护强度，$ϵ$越大，数据可用性越高，隐私保护强度越低。反之亦然。

3.4 拉普拉斯机制

实现差分隐私最简单的方式就是将拉普拉斯噪声注入到查询的结果中。

设查询为 $f(x)$ ，扰动后的查询为 $F(x)$ ，那么 $F(x)=f(x)+Lap(\frac{s}{ϵ})$

其中，$Lap(\frac{s}{ϵ})$ 是满足拉普拉斯分布的噪声。

$s$ 为全局敏感度，设 $D1$ 和 $D2$ 是两个相差只有一条记录的兄弟数据集，$Q$ 为查询函数。$s$ 等于任意两个兄弟数据集查询结果的$L_1$范数的最大值：
$$s=max||Q(D_1)-Q(D2)|{|}_1$$

3.5 符号定义

符号	描述
$D$	包含 n 条记录的数据集
$t_i=(x_i,y_i)$	数据集 D 中的第 i 条记录
$d$	特征向量 $x_i$ 的特征数
$\omega$	回归模型的权重向量
$f(t_i,\omega )$	回归模型的损失函数
$f_D(\omega )$	$f_D(\omega )={\sum }_{t_i\in D}f(t_i,\omega )$ | 对所有记录的损失函数求和
${\omega }^{\ast }$	${\omega }^{\ast }=argmi{n}_{\omega }{f}_D(\omega )$
${\bar{f}}_D(\omega )$	扰动后的$f_D(\omega )$
$\bar{\omega }$	${\bar{f}}_D(\omega )$ 最小时对应的权重$\omega$
$f_D(\omega )$	对 $f_D(\omega )$ 泰勒展开后得到的损失函数
$\omega$	$f_D(\omega )$ 最小时对应的权重$\omega$
$f_D(\omega )$	取泰勒展开式中的低次项构成的渐进函数
$\omega$	$f_D(\omega )$ 最小时对应的权重$\omega$
$\varphi$	$\omega$ 中的各个分量运算得到的结果（与二项展开式有关）如$({\omega }_1{)}^3\cdot {\omega }^2$
${\Phi }_j$	所有幂为 $j$ 的 $\varphi$ 对应的集合
${\lambda }_{{\varphi }_{t_i}}$	第 $i$ 条记录对应的 $\varphi$ 的多项式系数（这里有多个，因为 $\varphi$的幂有多个）

3.6 部分说明

• 设 $D$ 包含 $n$ 条记录 $t_1,t_2,...t_n$ ，每条记录包含 $n+1$ 个属性，$X_1,X_2...X_d,Y$。

  假设不失一般性， $\sqrt{{\sum }_{j=1}^d{x}_{ij}^2}\le 1$ （第 $i$ 条记录的特征的 L2 范数小于等于 1 ）

  这里我觉得是因为对数据做了规范化处理（均值为0，方差为1）

• 为了方便进行讨论，论文所有的属性都是二值属性，即 0 或 1 。如果有多值，比如婚姻状况，有未婚，已婚，丧偶三种。则将这个三值属性转换成两个二值属性，即是否已婚，是否丧偶。

4.理论部分

4.1 函数机制

直接在目标函数上进行扰动，极具挑战。这主要是因为权重 $\omega$ 的全局敏感度分析起来十分困难 。

根据 $Stone-Weierstrass$ 定理，任何连续可微分的函数 $f(x)$ 可以由一个多项式 $A{x}^n+B{x}^n-1...+K{x}^1+b{x}^0$来表示。

这样，在将原函数转换成多项式形式后。就可以在多项式系数上加入噪声，而不是在权重 $\omega$ 上加入噪声。

在回归问题中，对于训练集中的一条记录，目标函数为 $f(t_i,\omega )$ 。这里的 $\omega$ 就可以看作是 $f(x)$ 中的 $x$ 。

向量 $\omega$ 中包含 $d$ 个值 ${\omega }_1,{\omega }_2...{\omega }_d$，令 $\varphi$ 为 $\omega$ 中的各个分量幂运算得到的结果（这里与二项式定理有关）。

${\Phi }_j$ 为所有幂为 $j$ 的 $\varphi$ 对应的集合，公式表达如下：
$${\Phi }_j=\left\{\begin{array}{c}{\omega }_1^{c_1}{\omega }_2^{c_2}...{\omega }_d^{c_d}|{\sum }_{l=1}^d{c}_l=j\end{array}\right\}$$
例如，${\Phi }_0=\left\{\begin{array}{c}1\end{array}\right\}$ ，${\Phi }_1=\left\{\begin{array}{c}{\omega }_1,{\omega }_2...,{\omega }_d\end{array}\right\}$ ，${\Phi }_2=\left\{\begin{array}{c}{\omega }_i\cdot {\omega }_j|i,j\in [1,d]\end{array}\right\}$ 。

这里其实就是对 $\omega$ 求幂，${\omega }^0=1$ ，${\omega }^1=\left\{\begin{array}{c}{\omega }_1,{\omega }_2...,{\omega }_d\end{array}\right\}$，${\omega }^2=\left\{\begin{array}{c}{\omega }_i\cdot {\omega }_j|i,j\in [1,d]\end{array}\right\}$

设 $J$ 为多项式的最高次幂，$J\in [0,\infty ]$ ，${\lambda }_{{\varphi }_{t_i}}为多项式系数$， $f(t_i,\omega )$ 为可以由多项式表示为：
$$f(t_i,w)=\sum _{j=0}^J\sum _{\varphi \in {\Phi }_j}{\lambda }_{{\varphi }_{t_i}}\varphi (\omega )$$
因为函数机制是在多项式系数上加入拉普拉斯噪声，所以我们需要求解多项式系数的全局敏感度 $s$

对于兄弟数据集 $D$ 和 $D^{\prime }$，它们的目标函数可以由如下多项式表示：
$$\begin{gathered} f(t_i,\omega )=\sum _{j=0}^J\sum _{\varphi \in {\Phi }_j}\sum _{t_i\in D}{\lambda }_{{\varphi }_{t_i}}\varphi (\omega )， \\ f(t_i,\omega )=\sum _{j=0}^J\sum _{\varphi \in {\Phi }_j}\sum _{t_i\in D_1}{\lambda }_{{\varphi }_{t_i}}\varphi (\omega ). \end{gathered}$$
对它们的多项式作差，可得如下不等式：
$$\sum _{j=0}^J\sum _{\varphi \in {\Phi }_j}||\sum _{t_i\in D}{\lambda }_{{\varphi }_{t_i}}-\sum _{t_i^{\prime }\in D^{\prime }}{\lambda }_{{\varphi }_{t_i^{\prime }}}|{|}_1\le 2\underset{t}{\max }\sum _{j=1}^J\sum _{\varphi \in {\Phi }_j}||{\lambda }_{{\varphi }_t}|{|}_1$$
根据上述，可以得到函数机制的算法流程：

4.2 泰勒展开式

泰勒展开是用一个多项式函数 $g(x)$ 来仿造原函数 $f(x)$ 的方法，使这两个函数在某一点的初始值相等，$1$ 阶导数相等，$2$ 阶导数相等，… $n$ 阶导数相等。泰勒展开式在点 $x_0$ 处的表达式如下：
$$g(x)=g(x_0)+\frac{f^1(x_0)}{1!}x+\frac{f^2(x_0)}{2!}{x}^2+......\frac{f^n(x_0)}{n!}{x}^n$$
知乎上有个很好的帖子来理解泰勒展开式：怎样更好的理解并记忆泰勒展开式?

4.3 将函数机制应用到线性回归上

前面说到，函数机制用多项式来渐进目标函数，而线性回归的损失函数本身就是多项式，所以可以直接在损失函数的多项式系数上加噪声。

线性回归的目标函数:
$$\begin{gathered} f_D(\omega )=\sum _{t_i\in D}(y_i-x_i^T\omega {)}^2= \\ \sum _{t_i\in D}(y_i{)}^2-\sum _{j=1}^d\left(2\sum _{t_i\in D}{y}_i{x}_{ij}\right){\omega }_j+\sum _{1\le j,l\le d}\left(\sum _{t_i\in D}{x}_{ij}{x}_{il}\right){\omega }_j{\omega }_l \end{gathered}$$
全局敏感度求解如下：
$$\Delta =2\underset{t=(x,y)}{\max }\sum _{j=1}^J\sum _{\varphi \in {\Phi }_J}||{\lambda }_{{\varphi }_t}|{|}_1\le 2\underset{t=(x,y)}{\max }\left(y^2+2\sum _{j=1}^{d}y{x}_{(j)}+\sum _{1\le j,l\le d}{x}_{(j)}{x}_{(l)}\right)\le 2(1+2d+d^2)$$
$\because y\in [-1,1]\to max(y^2)=1,max(y{x}_j)=1$

将求解得到的全局敏感度 $\Delta$ 带入到算法1中即可求解。

4.4 将函数机制应用到 Logistic 回归上

$Logistic$ 回归的损失函数本身不是多项式，需要使用泰勒展开式构造一个多项式。

Logistic 回归的损失函数为：$f_D(w)=-[ylog{x}_i^T\omega +(1-y)log(1-x_i^T\omega )]$

论文证明在 Logistic 回归中泰勒展开到二阶就能保证构造的多项式函数相对于原函数损失只有 $\approx 0.015$

我们将 Logistic 回归的损失函数用泰勒在 $0$ 处展开到二阶（后面一项本身是多项式不需要展开）
$$f_D(\omega )=\sum _{i=1}^n\sum _{k=0}^2\frac{f_1^{(k)}(0)}{k!}{\left(x_i^T\omega \right)}^k-\left(\sum _{i=1}^n{y}_i{x}_i^T\right)\omega$$
对应的全局敏感度 $\Delta$ 为
$$\begin{gathered} \Delta =2\underset{t=(x,y)}{\max }\left(\frac{f_1^{(1)}(0)}{1!}\sum _{j=1}^d{x}_{(j)}+\frac{f_1^{(2)}(0)}{2!}\sum _{j,l}{x}_{(j)}{x}_{(l)}+y\sum _{j=1}^d{x}_{(j)}\right) \\ \le 2(\frac{d}{2}+\frac{d^2}{8}+d)=\frac{d^2}{4}+3d \end{gathered}$$
将 $\Delta$ 带入到算法1中即可求解

5. 避免注入的噪声使损失函数无法收敛

使用函数机制 $Logistic$ 回归中注入噪声，可能会导致损失函数无法收敛。

我们在对 $Logistic$ 进行低阶泰勒展开后，得到的是一个二阶多项式。

为了方便描述，我们令这个式子为$A{x}^2+bx+c$. 当 $A>0$ 时，损失函数为一个开口向上的抛物线。

如果加入对多项式系数扰动后，$A<0$ 那么损失函数就变成了一个开口向下的抛物线，那么就导致损失函数无法收敛到最小值处。

所以在 $Logistc$ 回归中需要保证多项式的二次项系数加噪后仍然为正。

论文中给出的一个解决方式是：如果发现 $A<0$ 了，重新运行函数机制，直到它扰动后为正。

6. 实验

作者将自己的算法与$DPME$，$Filter-Priority$，Truncated 以及不加差分隐私的算法进行了对比，结果证明函数机制造成的性能损失更小，训练时间更短，基本上是完胜其他几个算法（在我的论文里，你们是无法战胜我的）。

原作者使用的matlab进行实验且代码未公开，具体性能需要复现后才能知道。