基于深度学习的自然语言处理复习笔记 第五章
神经网络训练
与线性模型类似,神经网络也是可微分的参数化函数,它使用了基于梯度的优化算法来进行训练。非线性神经网络的目标函数并不是凸函数,因此使用基于梯度的优化方法可能会陷入局部极小。但是,基于梯度的优化方法在实际应用中仍然取得了良好的效果。
梯度计算是神经网络训练的核心。神经网络梯度计算的数学原理与线性模型,都是简单地利用微分地链式法则来进行计算。但是,对于复杂地网络来说,这个过程可能比较费力并且容易出错。幸运的是,梯度能够通过反向传播算法被有效和自动地计算得出。反向传播算法是一种使用链式法则来计算复杂式梯度的方法,期间可以缓存中间结果。更一般的说,反向传播算法是反向模式自动微分算法的特殊情况。接下来的部分描述了在计算图背景下的自动反向求微分模式。其余的章节主要致力于讲解在实践中训练神经网络的实用技巧。
5.1 计算图的抽象概念
虽然人们可以手工计算网络中各种参数的梯度,并在代码中实现他们,但这个过程繁琐且容易出错。对于大部分应用来说,优先考虑使用自动化工具来实现梯度计算。计算图的概念可以使我们轻松构建任意的网络,由它们的输入(前向传播)计算预测的输出,以及通过标量损失(反向传播)计算参数的梯度。
计算题是任意数学表达式的一种图表达结构。它是一个有向无环图(DAG),其中结点对应于数学运算或者变量,边对应于节点间计算值的流。图形结构在不同的组件之间根据依赖关系定义计算的顺序。计算图是一个DAG,而不是一棵树,一个操作的结果可以作为多个连续操作的输入。
由于神经网络本质上是一个数学表达式,因此它可以表示为计算图。例如,图5.1a代表了一个具有一个隐层和一个softmax输出变量层的MLP的计算图。在我们的符号中,椭圆代表数学运算或函数,而阴影矩形结点代表了参数。
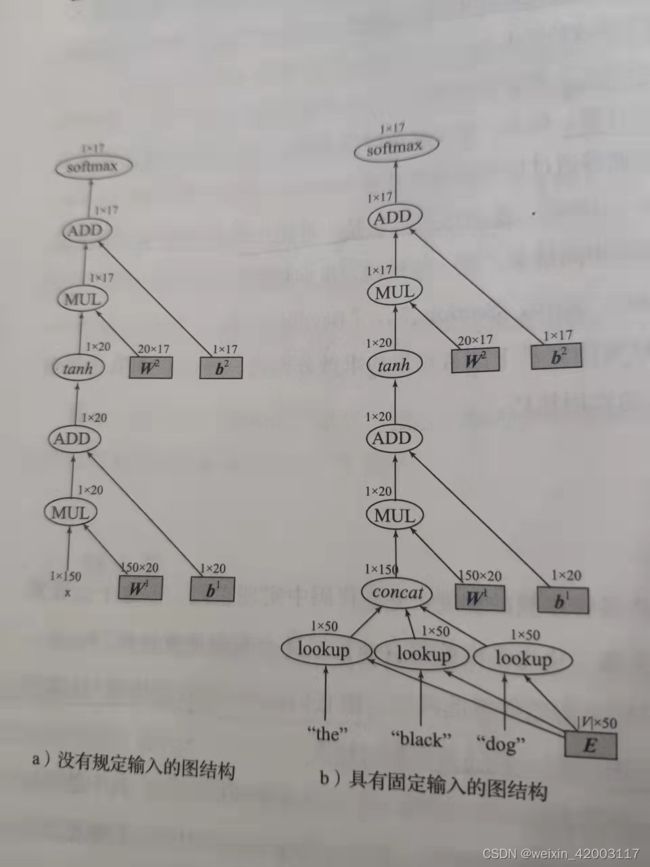
网络输入被视为常量,在图中绘制时不存在周围结点。输入和参数结点没有输入弧,输出结点没有传出弧。每个输出结点是一个矩阵,其维度标示在结点上方。
这个图是不完全的,没有指定输入,我们就不能得到输出,图5.1b显示了一个MLP的完全图,以三个单词作为输入,预测第三个单词的词性分布,这个图结构可以用来预测,但是不能用来训练,这时因为图的输出是一个向量(不是一个标量),并且该图没有考虑正确结果或是损失项。
一旦计算图建立完成,前向计算(计算输出结果)或反向计算(计算梯度)就可以直接运行了,计算过程如下所示。图的结构看起来可能令人畏惧,但是实际上可以通过使用专用软件库和API简单的实现。
5.1.1 前向计算
前向传递计算了图中结点的输出。由于每个结点的输出只依赖于它本身和传入的边,所以容易通过遍历拓扑顺序来计算所有结点的输出,并在给定前驱时,计算每个结点的输出。
更正式的讲,在有N个结点的图中,我们根据它们的拓扑顺序讲每个结点与下标i相关联。令f[i]为结点i的计算函数。令Π[i]作为结点i的父节点,让Π1 [i]={j|i∈Π[j]}作为结点i的子节点(这些为f[i]的参数),令v[i]为结点i的输出,也就是说,f[i]是作用于参数为Π2 [i]时的输出值。对于变量和输入结点来说,f[i]是一个常量函数并且Π3 [i]为空。计算图的前向过程计算出了所有结点的输出v[i],其中i∈【1,N】。
5.1.2 反向计算
反向传播过程开始于设置一个损失结点N,该结点拥有1*1的标量输出,然后进行前向传播计算直到到达结点N,根据节点值,反向传播过程计算了该结点参数的梯度。反向传播算法本质上就是使用链式求导法则。
5.1.3 软件
5.1.4 实现流程
使用计算图抽象概念和计算图结构,算法给出了一个网络训练算法的伪代码:
1、定义网络的参数
2、for iteration = 1 to T do
3、 for 数据集中的训练样本(x[i] , y[i] )
4、 loss_node <----build_ computation_graph(x[i], y[i],parameters)
5、loss_node.forward()
6、gradients <—loss_node().backward()
7、parameters<–update_parameters(parameters,gradients)
8、 return parameters
这里,build_computation_graph是一个用户自定义的函数,给定输入,输出和网络结构的情况下,它生成对应的计算图,返回单个损失结点。update_parameters是优化器特定的更新规则。流程指定为每个训练实例创建一个新的图形。这适用于在训练样例中变动的网络结构,例如循环神经网络和递归神经网络。对于固定结构的网络,如MLP创建一个基本计算图,只改变实例的输入和预期输出可能会更有效。
5.1.5 网络构成
只要网络的输出是向量,通过使一个网络的输出成为另一个网络的输入,那么创建任意网络是很简单的。计算图概念使这种能力变得具体:计算图中的每一个结点本身可以是一个具有指定输出结点的计算图。然后,可以设计任意深层复杂网络,并能轻松的评估和训练它们,这得益于自动的前向传播和梯度计算。这使得定义和训练循环神经网络和递归神经网络变得简单,也使得结构化输出和多目标训练的网络定义和训练变得简单。
5.2 实践经验
一旦进行梯度计算的时候,网络会使用SGD方法或者其他梯度的优化算法进行训练。由于被优化的函数并不是凸函数,所以很长一段时间神经网络的训练被称为黑科技,几乎没什么人能做到。事实上,许多参数影响着优化过程,所以必须注意调整这些参数。
5.2.1 优化算法的选择
虽然SGD算法效果很好,但是它收敛速度慢。由于大多数神经网络软件框架提供了这些算法的实现,所以很容易尝试不同的方法。我们发现,在训练更大的网络时,使用Adam算法非常有效,而且相对来说,对学习率的选择也是比较健壮的。
5.2.2 初始化
目标函数的非凸性意味着优化过程可能陷入局部极小或鞍点,从不同的初始点开始(比如,参数的不同随机值)可能产生不同的结果。因此,我们建议尝试几次从不同的随机初始化开始训练,选择其中一个在开发集上最好的结果。由于对不同的网络结构和数据集来说,不同的随机种子会导致最后结果的偏差,因此结果事先无法预料到。
随机数的大小对网络训练的成功与否具有非常大的影响。根据Glorot 和 Bengio,一个有效的方案叫做xavier初始化,其建议权重矩阵W∈R^ [d[in]]*^ [d[out]]以如下公式初始化:
W~U【- \sqrt{6}/\sqrt{d[in]+d[out]},+\sqrt{6}/\sqrt{d[in]+d[out]}】。其中U[a,b]是范围[a,b]的一个均匀采样。这个建议是基于tanh激活函数的性质提出的,在很多场景下都表现较好,也是很多人默认首先的初始化方法。
当使用relu非线性激活函数时,应该从均值为0,方差为\sqrt{2/d[in]]}的高斯分布采样进行权值初始化。,发现在图像分类任务中,这种初始化方法效果好于xavier方法,特别是在网络较深的时候。
5.2.3 重启与集成
在训练复杂网络时,不同的随机初始化可能会 导致不同的结果,表现出不同的精度,所以,如果计算资源允许,运行训练过程多次是比较明智的,每次都进行随机初始化,并在开发集中选择最好的一个。这种方法叫做随机重启。随机种子造成模型的平均准确率不同是比较有趣的,对分析过程稳定性也是一种暗示。
虽然初始化模型的时候,调整随机化种子比较烦人,但对于执行相同的任务,它还提供了一个简单的方法来获得不同的模型,即灵活使用模型集成。一旦有了多个模型,我们可以根据模型的集成而不是单个模型来预测(例如,通过不同模型的多数投票,或者将输出向量进行平均化作为集成模型的输出)。利用集成经常可以提高预测精度,但是代价是必须多次运行预测步骤(每个模型进行一次)。
5.2.4 梯度爆炸与梯度消失
在深层网络中,因为梯度通过计算图反向传播回来,错误梯度是非常常见的,要么梯度消失(变得非常接近0)要么梯度爆炸(变得非常高)。在更深的网络中,这个问题变得更加严重,尤其是在递归和循环神经网络中。处理梯度消失问题仍然是一个开放的研究问题。解决方法是有网络层变浅,逐步训练使用Batch-normalization方法(对每一个Minibatch,让网络中的输入归一化均值为0且单位方差的分布),或者使用特定的结构去帮助梯度流动(例如,循环神经网络的LSTM和GRU结构)。处理梯度爆炸有一个简单但是高效的办法,如果它们的范数超过给定的阈值,就裁剪掉。g^代表网络中所有参数的梯度,| g^ |为它的L2范数。Pascanu等人建议如果|g ^|>threshold,则令g ^为threshold/|g ^|。
5.2.5 饱和神经元与死神经元
带有tanh与sigmoid激活函数的网络层往往容易饱和——造成该层的输出都接近于1,这是激活函数的上界。饱和神经元具有很小的梯度,所以应该避免。带有relu激活函数的网络层不会饱和,但是会坏死——大部分甚至所有的值为负值,因此对于所有的输入来说都裁剪为0,从而导致该层梯度全为0。如果你的网络没有训练好,检查网络层的饱和神经元和死神经元是明智的。饱和神经元是由于值太大的输入层引起的,可以通过更改初始值,缩放输入值的范围和改变学习率来控制。死神经元是由于进入网络层的负值引起的,减小学习率将缓解这种现象。对于饱和层来说,另一种选择是归一激活函数后的饱和值,例如使用g(h)=tanh(h) / |tan(h)|而不是g(h)=tanh(h)。归一化是对抗饱和神经元的有效方法,但是在梯度计算过程中代价较大。一个相关的技巧为batch normalization,对每一层激活函数后的值进行归一化,在每个Mini-batch中均值为0,方差为1.在计算机视觉中,batch normalization已经成为深层网络训练一个关键的组成部分,这篇文章还提到,在NLP应用中,它并没有那么受欢迎。
5.2.6 随机打乱
网络读入训练样本的顺序是很重要的。上面提到的SGD算法在每轮迭代中随机选取一个样例,在实践中,大多数实现都以随机顺序训练样本,基本上都是执行随机抽样。
5.2.7 学习率
学习率的选择是重要的,太大的学习率会阻止网络收敛到一个有效的解,太小的学习率则需要长时间来收敛。一个经验法则是,实验应该从范围[0,1]内尝试初始学习率,比如0.001,0.01,0.1,1。观测网络的loss值,一旦loss值在开发集上停止改动,则降低学习率。学习率速率可以看作minibatch数量的函数。一个常见的表示是将初始速率除以迭代次数。Leon Bottou建议使用\eta[t]=\eta [0] (1+\eta [0]λt)[-1]作为学习率的表达式,其中\eta [0]为初始的学习率,\eta [t]为第t个训练样本的学习率,λ为额外的超参数。他还建议在运行整个数据集之前,通过少量数据决定一个较好的\eta [0]。
5.2.8 minibatch
在每个训练样本(minibatch大小为1)或者每K个训练样本结束后更新参数。大的minibatch训练对有些问题是有益的。在计算抽象图时,每K个训练样例创建一个计算图,然后将k个损失节点连接到一个计算平均值的结点,它的输出作为minibatch的损失。专门的计算架构如GPU对大的minibatch数据训练也有帮助,通过矩阵运算来取代矩阵向量运算。这部分内容超出了本书的范围。
-1 ↩︎
-1 ↩︎
-1 ↩︎