分类准确度
1、分类准确度和混淆矩阵
1.1 分类准确度存在的问题
假如有一个癌症预测系统,输入体检信息,可以判断是否有癌症,准确度为99.9%,这个系统是好还是坏?
如果癌症产生的概率本来就只有0.1%,那么即使不采用此预测系统,对于任何输入的体检信息,都预测所有人都是健康的,即可达到99.9%的准确率。如果癌症产生的概率本来就只有0.01%,预测所有人都是健康的概率可达99.99%,比预测系统的准确率还要高,这种情况下,准确率99.9%的预测系统是失败的。
由此可以得出结论:对于极度偏斜(Skewed Data)的数据,只使用分类准确度是远远不够的。
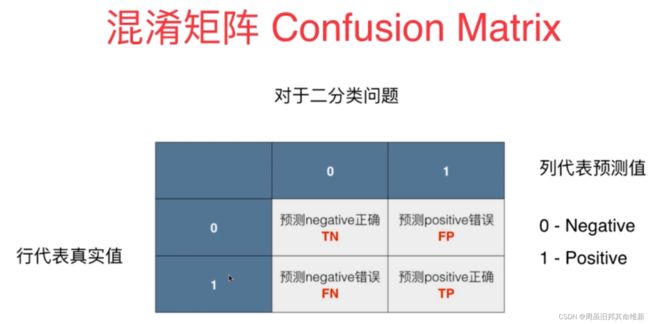
1.2 混淆矩阵
1.3 代码实现混淆矩阵
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
# 模型准确度
print(log_reg.score(X_test, y_test))
y_predict = log_reg.predict(X_test)
def TN(y_true, y_predict):
return np.sum((y_true == 0) & (y_predict == 0))
def FP(y_true, y_predict):
return np.sum((y_true == 0) & (y_predict == 1))
def FN(y_true, y_predict):
return np.sum((y_true == 1) & (y_predict == 0))
def TP(y_true, y_predict):
return np.sum((y_true == 1) & (y_predict == 1))
# 混淆矩阵
def confusion_matrix(y_true, y_predict):
return np.array([
[TN(y_true, y_predict), FP(y_true, y_predict)],
[FN(y_true, y_predict), TP(y_true, y_predict)]
])
print(confusion_matrix(y_test, y_predict))
# 精准率
def precision_score(y_true, y_predict):
tp = TP(y_true, y_predict)
fp = FP(y_true, y_predict)
try:
return tp / (tp + fp)
except:
return 0.0
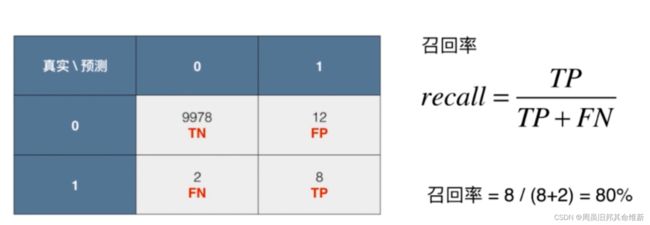
# 召回率
def recall_score(y_true, y_predict):
tp = TP(y_true,y_predict)
fn = FN(y_true,y_predict)
try:
return tp / (tp + fn)
except:
return 0.0
print(precision_score(y_test, y_predict))
print(recall_score(y_test,y_predict))
sklearn中的混淆矩阵:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
y_predict = log_reg.predict(X_test)
print(confusion_matrix(y_test, y_predict))
print(precision_score(y_test,y_predict))
print(recall_score(y_test,y_predict))
# 调和平均值,见2.1
print(f1_score(y_test,y_predict))
2、精准率和召回率的平衡
2.1 调和平均值
精准率和召回率是此消彼长的,即精准率高了,召回率就下降,在一些场景下要兼顾精准率和召回率,就有 F1 score。
F1值是来综合评估精确率和召回率,当精确率和召回率都高时,F1也会高
代码实现:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
# 获得数据的预测得分值
decision_scores = log_reg.decision_function(X=X_test)
# print(decision_scores)
# 分值大于5则预测事件发生
y_predict_d = np.array(decision_scores > 5, dtype=int)
print(confusion_matrix(y_test,y_predict_d))
print(precision_score(y_test,y_predict_d))
print(recall_score(y_test,y_predict_d))
# 分值大于-5则预测事件发生
y_predict_d = np.array(decision_scores > -5, dtype=int)
print(confusion_matrix(y_test,y_predict_d))
print(precision_score(y_test,y_predict_d))
print(recall_score(y_test,y_predict_d))
2.2 precision_recall曲线
使用sklearn绘制精准率召回率曲线(也叫PR曲线):
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_recall_curve
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
# 获得数据的预测得分值
decision_scores = log_reg.decision_function(X=X_test)
precission, recall, thresholds = precision_recall_curve(y_test, decision_scores)
plt.plot(thresholds, precission[:-1])
plt.plot(thresholds, recall[:-1])
plt.show()
如果A模型的PR曲线整体在B模型的外面,则说明A模型优于B模型。也可以说模型的PR曲线和X、Y轴包含的面积越大,则模型越好。
2.3 ROC曲线
ROC曲线描述的是TPR 和 FPR 之间的关系。
TPR = 召回率 = TP/(TP+FN)
TPR即预测为1且预测正确,占真实值为1的百分比
FPR = FP/(TN + FP)
FPR即预测为1且预测错误,占真实值为0的百分比
代码实现:
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
# 获得数据的预测得分值
decision_scores = log_reg.decision_function(X=X_test)
fpr, tpr, thresholds = roc_curve(y_test, decision_scores)
plt.plot(fpr, tpr)
plt.show()
# roc_auc_score即roc_curve的面积
print(roc_auc_score(y_test, decision_scores))
roc_auc_score对极度偏斜的数据不敏感,极度偏斜的数据还是需要看精准率和召回率,roc_auc_score主要用来比较模型的好坏,面积更大表明模型更好。
3、多分类问题中的混淆矩阵
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_score
from sklearn.metrics import confusion_matrix
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.8)
log_reg = LogisticRegression()
log_reg.fit(X=X_train, y=y_train)
print(log_reg.score(X_test,y_test))
y_predict = log_reg.predict(X_test)
print(precision_score(y_test,y_predict,average="micro"))
# 多分类(手写数字识别)中的混淆矩阵第i行表示真实值是数字几,第j列表示预测值是数字几
print(confusion_matrix(y_test,y_predict))