numpy实现周志华机器学习 9.5 密度聚类（DBSCAN算法）

本文主要参考周志华《机器学习》的9.6章节，对密度聚类做简单介绍，并使用numpy对具有代表性的DBSCAN密度聚类算法进行实现。
1、何为密度聚类？
密度聚类顾名思义是一种基于密度的聚类方法，

此类算法假设聚类结构能通过样本分布的紧密程度确定，通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。 ----《机器学习》

可能看到上述的解释，大家还无法理解什么是密度聚类。不要着急，看完下面的DBSCAN算法，你就明白了。
2、DBSCAN算法
DBSCAN是其中的一种著名算法。理解DBSCAN算法之前，要理解一个重要概念，即密度可达。理解这个概念，我们可以想象古代的驿站送信，每一个驿站我们可以当做是一个元素，马匹到了一个驿站之后，换驿站中的另外的马匹继续送信。如果首都在长安，我们就把长安作为核心对象，长安的信件可以送到的地方，就是这个核心对象密度可达的集合。在聚类中我们就把其视作一类。

大概知道了这个算法的核心思想之后，我们要考虑怎么数学抽象，怎么编程实现？该算法用两个参数（ε，minPts）来确定了一个领域的概念。ε可以理解为每匹马可以跑的里程就是ε，定义了领域的半径，minPts定义了邻域内的最小元素数目。为什么要有一个minPts呢？试想，如果没有这个限制，那么每一个元素都可以是一个领域。

根据领域的概念，密度可达即为:$$对X_i与X_j，若存在样本序列P_1,P_2,...,P_n，$$$$其中P_1=x_i,P_n=x_j且P_i+1在以P_i为核心对象的领域中，则称x_j有x_i密度可达$$

如果上面讲的不是很懂，可以先看看下面的算法伪代码：

3、算法的总结和优缺点
算法的思路是：

1. 先找到所有的核心对象
2. 每一个核心对象找到其密度可达的样本。

优点：去除掉了噪音的影响
劣势：邻域和minpts的参数选择

numpy 实现：

import numpy as np
def distance(a, b, p):
    return np.sum((a - b) ** p) ** (1 / p)


class DBSCAN(object):
    def __init__(self, epsilon, minPts):
        """
        初始化超参数
        :param epsilon: epsilon is the min distance 确定领域的最小距离
        :param minPts: minPts is the min elements. 确定领域的最少元素数目
        """
        self.minPts = minPts
        self.eps = epsilon
        self.X = None
        self.ker = None
        self.k = None
        self.gama = None
        self.omega = None
        self.num = None
        self.dim = None
        self.distMatrix = None
        self.labels = None

    def _update_omega(self):
        """
        确定核心对象的omega集合，
        :return:
        """
        for j1 in range(self.num):
            count = 0
            for j2 in range(self.num):
                dist = distance(self.X[j1, :], self.X[j2, :], 2)
                self.distMatrix[j1, j2] = dist    # 生成距离矩阵
                if dist <= self.eps:
                    count += 1
            if count >= self.minPts:
                self.omega[j1] = 1   # 核心对象的标签设置为1

    def _find_nodes(self):
        """
        找到所有核心对象的密度可达的节点，并将其作为一个聚类簇
        :return:
        """
        while np.sum(self.omega) > 0:         # 当核心对象的数目不为0时，执行下面代码
            index = np.argwhere(self.omega == 1)
            rand = np.random.choice(index.shape[0])
            obj_index = index[rand]        # 随机选择的核心对象的样本编号
            Q = [obj_index]                # 初试化队列Q,只包含随机选择的一个核心对象
            self.gama[obj_index] = -1      # 将未访问的样本集合中的上一步选择的对象的编号设置为-1，表示已选择
            while len(Q) > 0:  # 当初始化队列Q不为空，执行以下代码
                q = Q[0]
                Q = Q[1:]   # 从Q中取出第一个样本q
                dists = self.distMatrix[q, :]
                count = np.argwhere(dists <= self.eps).shape[0]  # 找到该样本的领域中的元素个数
                # print(np.argwhere(dists <= self.eps))
                # print(count)
                # print("*"*19)
                if count >= self.minPts:   # 如果该样本满足领域的个数限制，执行下面代码
                    self.omega[q] = 0
                    delta = []
                    for i in np.argwhere(dists < self.eps):
                        # print(i[-1])
                        if i[-1] in self.gama:
                            Q.append(i[-1])            # 将该样本领域中的元素与未标记的样本取交集，并添加到Q队列中
                            self.gama[i[-1]] = -1      # 将交集中的元素标记为已经访问
            self.labels[self.gama == -1] = self.k  # 生成聚类簇，类编号为k，类中的元素为第一次随机选择的和新对象，所有密度可达的元素
            self.gama[self.gama == -1] = -2   # 将本次循环中访问对象的标签设为-2，表示已访问并且分类。
            self.k += 1  # 类编号+1
            # break

    def fit(self, X):
        # 初始化参数
        self.X = X
        self.k = 1                  # 类编号
        self.num = X.shape[0]       # 样本数
        self.omega = np.zeros(self.num)  # 核心对象的集合
        self.gama = np.arange(0, X.shape[0])  # 未访问的样本集合
        self.distMatrix = np.zeros((self.num, self.num))  # 距离矩阵
        self.labels = np.zeros(X.shape[0])  #类标签
        # 初始化核心对象集合
        self._update_omega()
        # print(np.sum(self.omega))
        # 根据密度可达划分聚类簇
        self._find_nodes()


if __name__ == '__main__':
    import matplotlib.pyplot as plt
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    # Generate some data
    from sklearn.datasets.samples_generator import make_blobs

    X, y_true = make_blobs(n_samples=400, centers=4,
                           cluster_std=0.60, random_state=0)
    X = X[:, ::-1]  # flip axes for better plotting
    
    fig, axs = plt.subplots(1,2)
    model = DBSCAN(0.6, 10,)
    model.fit(X, )
    my_label = model.labels
    ax1 = axs[0]
    ax1.scatter(X[:, 0], X[:, 1], c=my_label, s=40, cmap='viridis')
    ax1.set_title("My DBSCAN")
    
    from sklearn.cluster import DBSCAN
    db = DBSCAN(eps=0.6, min_samples=10).fit(X)
    ax2 = axs[1]
    ax2.scatter(X[:, 0], X[:, 1], c=db.labels_, s=40, cmap='viridis')
    ax2.set_title("scipy DBSCAN")
    plt.show()

运行结果：

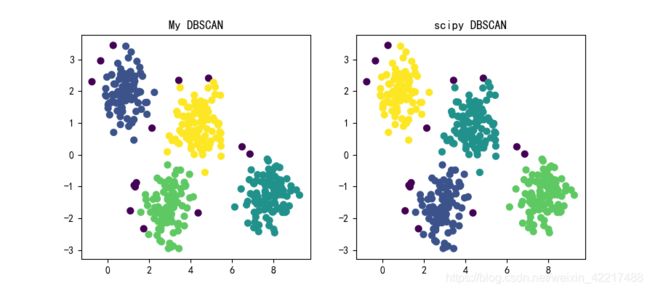
其中紫色的点是每一个核心对象密度不可达的元素，可以视为噪音。可以看到，就结果方面，和scipy库中的效果相差不多。

tips：第一次写文章，哪里写得不好，大家多多包涵。如果哪里有疑问，欢迎留言。此外，我将继续有间断用numpy实现周志华《机器学习》的算法，欢迎大家关注。