二分查找及例题

---

二分查找的板子

这两个板子要牢牢的记住形成肌肉反射

def search(l ,r):
	while l < r:
		mid = (l+r) // 2
		if (check(mid)): r = mid
		else: l = mid + 1
	return r

def search(l, r):
	while l < r:
		mid = (l+r+1) // 2
		if (check(mid)): l = mid
		else: r = mid - 1
	return l
		

看 check(mid）的逻辑定用哪个板子, 我们假定return r 的是模板1，return l的是模板2（本篇文章下面都这样称呼）

704.二分查找

题目链接
比如用板子写这道题，如果check(mid) 的逻辑是 nums[mid] >= target,
我们应该在左区间找，r = mid，因此是用模板1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums)-1
        while l < r:
            mid = (l+r) // 2
            if nums[mid] > target: r = mid
            else: l = mid + 1
        return r if nums[r] == target else -1

如果 check(mid) 的逻辑是 nums[mid] > target，应该在左区间找，但是 r = mid -1吧，target肯定取不了r，因此是模板2

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums)-1
        while l < r:
            mid = (l+r+1) // 2
            if nums[mid] > target: r = mid-1
            else: l = mid
        return l if nums[l] == target else -1

367.有效的完全平方数

题目链接
这完全就是套板子就行

def isPerfectSquare(self, num: int) -> bool:
        l, r = 0, num
        while l < r:
            mid = (l+r) // 2
            if mid**2 >= num: r = mid
            else: l = mid+1
        return True if r**2 == num else False

69. x的平方根(板子2的逻辑)

题目链接
这道题我们可以用枚举整数来查找，如果这道题用板子1，写出来就是有问题的，为什么呢？
错误代码逻辑

def mySqrt(self, x: int) -> int:
        l, r = 0, x
        while l < r:
            mid = (l+r) // 2
            if mid**2 >= x: r = mid
            else: l = mid + 1
        return r

这样写是有问题的，因为我们这道题的答案是小于等于目标的，如果说我们check(mid),判成 if mid2 >= x: r = mid, 我们找到的值会是大于等于目标值里最小的，比如输入8，找出3，我们反正是不能太大
我们应该要找小于等于目标值里最大的**，所以要从[mid, …]里找
所以check()要写成， if mid ** 2 <= x: l = mid
要用板子2才能过

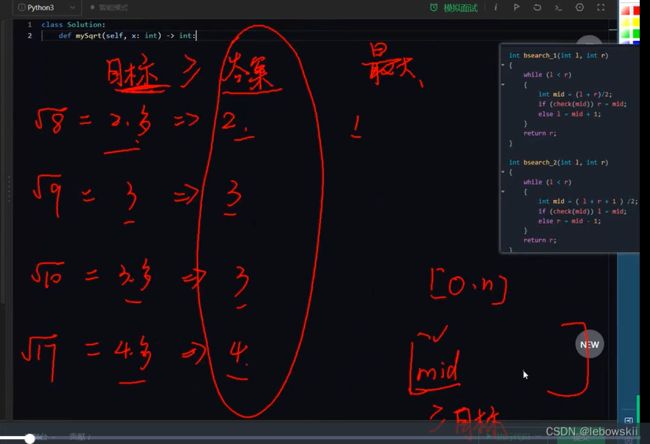
正确代码逻辑

def mySqrt(self, x: int) -> int:
        l, r = 0, x
        while l < r:
            mid = (l+r+1) // 2
            if mid**2 <= x: l = mid
            else: r = mid - 1
        return l

35.搜索插入位置

题目链接
洛克哥说，一定要对大于等于的最小，小于等于的最大这种感觉敏感起来，一般都是二分，可能我现在实力还没有体会吧

那么这道题，其实找的是什么呢？找的是，大于等于target的最小下标，那我r =mid, 是不是模板1啊 […mid], 直接套，不用改动, 但是初始化 r = len(nums), 要扩容，因为如果加在队尾的话，这样直接就是对的了

def searchInsert(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums)
        while l < r:
            mid = (l+r) // 2
            if nums[mid] >= target: r = mid
            else: l = mid + 1
        return r

如果是模板2的话，找的是什么，找的是小于等于target的最大下标，由于找的是小于等于的，所以如果没有target需要插入的话，返回的是 l + 1, 并且还要特判加载首部

def searchInsert(self, nums: List[int], target: int) -> int:
        if target <= nums[0]: return 0
        l, r = 0, len(nums)-1
        while l < r:
            mid = (l+r+1) // 2
            if nums[mid] <= target: l = mid
            else: r = mid - 1
        return l if nums[l] == target else l+1

这种因为是找的是 小于等于target 的，插入时要返回 l +1，所以一开始不用扩容
例如 nums = [1,3,5,6], target = 2
模板2等于说找的是 1 对应的下标，但是模板1找的是3对应的下标，所以不用特判

278. 第一个错误的版本

题目链接
直接就是遇到错误了，我们从[…mid]中找，直接套用模板1 二分查找

744.寻找比目标字母大的最小字母

题目链接
找的是比目标字母大的 最小字母，那么是不是check mid满足条件比目标值大，然后从左区间找
直接套用模板1
但是注意如果target大于区间右边界，要循环到区间首部

 def nextGreatestLetter(self, letters: List[str], target: str) -> str:
        if target >= letters[-1]: return letters[0]
        l, r = 0, len(letters)-1
        while l < r:
            mid = (l+r) // 2
            if letters[mid] > target: r = mid
            else: l = mid+1
        return letters[r]

162.寻找峰值

题目链接
这道题怎么用二分查找呢？我其实有些迷惑, 而且题意直接要求用logn的算法来解，那不是直接就是二分么
看了代码好像有点明白了，这个题里的数算是有序的，从小到大，遇到峰值，然后降序，那么找到大于等于nums[i+1], 我们左区间找

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l < r:
            mid = (l + r) // 2
            if nums[mid] >= nums[mid+1]:
                r = mid
            else: l = mid + 1
        return r

875.爱吃香蕉的珂珂

题目链接
珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数。

示例 1：
输入：piles = [3,6,7,11], h = 8
输出：4
示例 2：
输入：piles = [30,11,23,4,20], h = 5
输出：30
示例 3：
输入：piles = [30,11,23,4,20], h = 6
输出：23

提示：
1 <= piles.length <= 10^4
piles.length <= h <= 10^9
1 <= piles[i] <= 10^9

思路

这个题也是一种二分，但它不是在数组上二分，而是在答案上（在这道题里就是吃香蕉的速度上）二分，就是二分去找k

比如一个数组 [3, 6, 7, 11], h = 4, 我以 k = 8去吃， 需要5个小时，所以不符合要求，所以 我以 k=7, 是不是更不符合要求了， 所以我们应该从 [mid …]去找，这就是二分的感觉了

用二分去找k

如果说我们check(mid) 是可以在h小时内吃完的，那么我们从[…mid]去找，找能够满足条件的最小值, 那是不是应该从左区间找小的
只不过这个check需要我们自己去写一下，遍历一下，看看以x速度能否在h小时内吃完

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        def check(x):
            cnt = 0
            for pile in piles:
                cnt += pile // x
                if pile % x != 0: cnt += 1
            return cnt <= h
        
        l, r = 1, max(piles)
        while l < r:
            mid = (l+r) // 2
            if check(mid): r = mid
            else: l = mid + 1
        return l

410.分割数组的最大值 (困难)

题目链接
各自的最大值最小，触发关键词，应该是用二分的题，但是怎么用二分呢？在什么区间上二分呢？

应该是在0到sum(nums),这个区间上，找一个尽量小的（模板1）

但是我们在二分的时候 if check(mid), 让这个mid 是 m个 子数组和 的最大值

这个if check(mid, nums, k)的逻辑确实难。所以这道题才是困难吧

def splitArray(self, nums: List[int], k: int) -> int:
        def check(x, nums, k):
            cnt, cur = 1, 0
            for i in range(len(nums)):
                if cur + nums[i] <= x: cur += nums[i]
                else:
                    if nums[i] > x: return False
                    cur = nums[i]
                    cnt += 1
            return cnt <= k
        
        sum_ = sum(nums)
        l, r = 0, sum_
        while(l < r):
            mid = (l + r) // 2
            if check(mid, nums, k): r = mid
            else: l = mid + 1
        return r

34.在排序树组查找元素第一个和最后一个位置

题目链接
第一个字母肯定是大于等于target的最小的，最后一个肯定是小于等于target的最大的，分别对应模板1和模板2，直接套就行了

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if nums == []: return [-1, -1]
        res = []
        
        l, r = 0, len(nums)-1
        while l < r:
            mid = (l+r) // 2
            if nums[mid] >= target: r = mid
            else: l = mid+1
        if nums[r] == target: res.append(r)
        else: return [-1,-1]
        
        l, r = 0, len(nums)-1
        while l < r:
            mid = (l+r+1) // 2
            if nums[mid] <= target: l = mid
            else: r = mid - 1
        res.append(l) 
        return res 

436.寻找右区间（较难）

题目链接
题目大意 这题迫切需要一个语文课代表翻译一下题目。

题目给了一个数组 intervals，其中的每个元素都是一个区间。

当区间 BB 的起点 大于等于 区间 AA 的终点，我们就说区间 BB 在区间 AA 的右侧。

让我们求每个区间的右侧第一个区间（右侧的区间中，起点最小的那个）。

如果还不好理解，请看下面两张图。
示例二 intervals = [[3,4],[2,3],[1,2]]

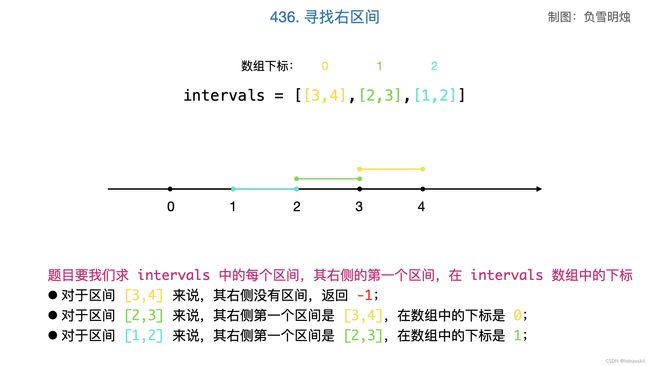
示例三 intervals = [[1,4],[2,3],[3,4]]

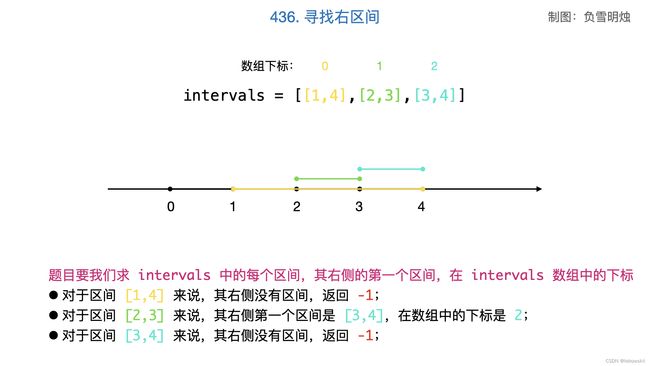
等于说，找到大于等于区间右端的最小右区间
难点：
1.如果用二分，肯定要有序，冥冥之中感觉肯定要以每段左端点排序
但是排序之后，遍历的时候，如何往结果里加入原来区间在intervals中的位置？
2.二分模板的选择，找到大于等于当前interval的右端点的最小左端点，并且把它所在的idx放进结果里，那么找不到的话，怎么处理才能让结果里呈现-1？

思路：
1.先对 interval进行排序（左端点），为了能够在结果集里呈现原来顺序的idx，需要把原始的元祖加一个idx,这样排序之后原序也能找到

2.排序之后，对每个区间interval遍历，进行二分查找，l, r分别是 0， len(intervals), 找的是大于等于当前interval的右端点的最小左端点的所在下标r, 用的是模板1

3.找到之后，要改变的是原序位置映射在res中的下标的值，如果找到的intervals[r][0] >=intervals[i][1] 则改变原序位置在res中的值，改为原序中第一个右区间的下标，否则找不到这样的最小右区间，-1

class Solution:
    def findRightInterval(self, intervals: List[List[int]]) -> List[int]:
        for i, interval in enumerate(intervals):
            interval.append(i)
        intervals.sort()
        res = [-1]* len(intervals)
        for i in range(len(intervals)):
            l, r = 0, len(intervals)-1
            while l < r:
                mid = (l+r) // 2
                if intervals[mid][0] >= intervals[i][1]: r = mid
                else: l = mid+1
            res[intervals[i][2]] = intervals[r][2] if intervals[r][0] >=intervals[i][1] else -1
        return res

力扣官方给的代码更容易理解

def findRightInterval(self, intervals: List[List[int]]) -> List[int]:
        for i, interval in enumerate(intervals):
            interval.append(i)
        intervals.sort()

        n = len(intervals)
        ans = [-1] * n
        for _, end, id in intervals:
            i = bisect_left(intervals, [end])
            if i < n:
                ans[id] = intervals[i][2]
        return ans

网易笔试题 (和410分割数组最大值一个套路)

题目描述

小易是养猪大户,尤其喜欢黑猪,小易养的这些猪都有一个特点,只要他们靠太近就会不开心,从而影响感，所以人小易需要把他们分开饲养。现在小易有N间猪舍和M头猪,猪舍排在一条直线上,第间猪舍在Xi的位置,每1个猪舍只能容纳1头猪。
为了提高猪的品质,小易决定把每头猪都放在离其它猪尽可能远的猪舍。也就是要最大化最近的两头猪之间的距离。
当然,为了节约成本,我们不能建太多猪舍,但又不能让猪靠太近，所以我们要让两头猪之间的最小距离尽可能的大，那么,这个最大的最小距离是多少呢?

输入描述:
输入包括多行。
第一行用空格分隔的两个整数n和M: 1< m < n < 100000
第二行为N个用空格隔开的整数。表示位置Xi，1<=XI<=100000
输入
5 3
1 9 8 4 2
输出
3

说明
把猪放在1，4，8这样最小距离是3。

题解

触发关键词，最小距离尽可能大，那么二分模板使用第二个

n, m = map(int, input().split())
nums = list(map(int, input().split()))
nums.sort()

class solution:
    def check(self,x):
        cnt, pre = 1, nums[0]
        for i in range(1,n):
            if nums[i] - pre >= x:
                cnt += 1
                pre = nums[i]
        return cnt >= m

    def search(self,nums):
        l, r = 0, nums[n-1] - nums[0]
        while l < r:
            mid = (l + r + 1) // 2
            if self.check(mid): l = mid
            else: r = mid -1
        return r

a = solution()
print(a.search(nums))

题目描述：
餐厅同时有多份餐食必须在H小时内送到顾客手中。餐厅的第i个餐食的大小为size[i]，每一小时餐厅会按照下单顺序，按照体积大小给外卖配送员的外卖箱中放置餐食，装载的体积不会超过该箱子的最大容积。每一小时能送完一趟回餐厅继续装载配送，返回能在H小时内运送外卖的最低运载能力。已知1≤H≤size.length≤10000,1≤size[i]≤100
输入描述
size=[1,2,3,4,5,6,7,8,9,10],H=3
要想在三小时内送完，则箱子的容积最小为21，具体如下：
第一小时：1,2,3,4,5,6
第二小时：7,8
第三小时：9,10
输出描述
21
样例输入
1,2,3,4,5,6,7,8,9,10 3
样例输出
21

1235.规划兼职工作

题目链接