代码验证约瑟夫环百科词条中的故事(Python)——约瑟夫斯的故事、数学家加帕斯讲的故事,体验算法模板的奇妙。
Python 官网:https://www.python.org/
-
Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅是基础那么简单……
- My CSDN主页、My HOT博、My Python 学习个人备忘录
- 好文力荐、 老齐教室
自学并不是什么神秘的东西,一个人一辈子自学的时间总是比在学校学习的时间长,没有老师的时候总是比有老师的时候多。
—— 华罗庚
这是我参加“14天阅读挑战赛”第二周第3篇
点击查看“14天阅读挑战赛”详情
前面发布的学习笔记《Py递归解“约瑟夫”的一种变形问题》,其实也是可以用for来实现的。
代码
def j(n):
'''用for循环解“约瑟夫环”一种变形问题。\n 约瑟夫环的一种变形。我们考虑的问题是开始时有n个人,记为1到n,站成一个圆圈。每一步,每第2个人将被去除,直到只剩下一个人为止。我们把剩下的人记为J(n),用程序求出1≤n≤16的J(n)。'''
persons = list(range(1, n+1))
k = [0] # 确定第一个被删除人的位置。
while len(set(persons)) > 2:
# print(persons) #调试用语句。
for i in range(len(persons)):
if len(set(persons)) == 2:
break
if k[0] != 0 and persons[i] != 0:
#print(persons[i], end=', ')
persons[i] = 0
k[0] = 0
else:
k[0] = 1
persons = list(set(persons))
if 0 in persons:
persons.remove(0)
# input(persons) # 调试用语句。
return persons[0]
运行代码输出:
/sdcard/qpython $ python 1234.py
用for循环解“约瑟夫环”一种变形问题。
约瑟夫环的一种变形。我们考虑的问题是开始时有n 个人,记为1到n,站成一个圆圈。每一步,每第2个人将 被去除,直到只剩下一个人为止。我们把剩下的人记为J(n),用程序求出1≤n≤16的J(n)。
去除人位置顺序:
当队列为 1人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为 2人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为 3人时,约瑟夫环最后剩下的是第 3人。
去除人位置顺序:
当队列为 4人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为 5人时,约瑟夫环最后剩下的是第 5人。
去除人位置顺序:
当队列为 6人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为 7人时,约瑟夫环最后剩下的是第 7人。
去除人位置顺序:
当队列为 8人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为 9人时,约瑟夫环最后剩下的是第 9人。
去除人位置顺序:
当队列为10人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为11人时,约瑟夫环最后剩下的是第11人。
去除人位置顺序:
当队列为12人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为13人时,约瑟夫环最后剩下的是第13人。
去除人位置顺序:
当队列为14人时,约瑟夫环最后剩下的是第 1人。
去除人位置顺序:
当队列为15人时,约瑟夫环最后剩下的是第15人。
去除人位置顺序:
当队列为16人时,约瑟夫环最后剩下的是第 1人。循环用时0.001482秒。~~~~~~~~~~~~~~ 2022-10-27 18:14:56 ~~~~~~~~~~~~~~~
Josephus(约瑟夫斯)的故事(点此跳转“约瑟夫环”百科词条)
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。
然而Josephus和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。
问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
代码
def josephus_story(n=41, k=1, m=3):
''' Josephus的故事:\n 据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。\n 然而Josephus和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。\n 问题是,Josephus and his friend,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。'''
persons = list(range(1, n+1))
def eliminate(k, m):
''' 从第k人开始,步长为m淘汰人。'''
if len(persons) == 2:
return
k += m -1
while len(persons) < k:
k -= len(persons)
print(persons.pop(k-1), end=', ')
eliminate(k, m)
eliminate(k, m)
return persons
数字家Gapas(加帕斯)讲的故事(点此跳转“约瑟夫环”百科词条)
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:
30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。
递归代码
def gapas_story(n=30, k=1, m=9):
'''数学家Gapas(加帕斯)讲的故事:\n 17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:\n 30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。'''
persons = list(range(1, n+1)) # 用1~n的数组表示30人的队列。
def resursive_work(k, m):
''' 递归算法工作函数。'''
if len(persons) == 15: # 终止递归。
return
k += m-1 # 非教徒位置计算。
while k > len(persons):
k -= len(persons) # while 循环处理大于列表长度的情况。
print(persons.pop(k-1), end=', ') # k 位置的人在列表中下标为 k-1 。
resursive_work(k, m) # 递归调用。
resursive_work(k, m) # 调用函数开始递推。
return(', '.join(map(str, persons))) # 返回教徒应处位置。
循环代码
def gapas_story(n=30, k=1, m=9):
'''数学家Gapas(加帕斯)讲的故事:\n 17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:\n 30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。'''
persons = list(range(1, n+1)) # 用1~n的数组表示30人的队列位置。
while len(persons) > 15:
k += m-1 # 定位非教徒。
while k > len(persons):
k -= len(persons) # while 处理 k 大于列表长度。
print(persons.pop(k-1), end=', ') # 推非教徒下水。
return ', '.join(map(str, persons)) # 返回教徒应处位置列表。
标准“约瑟夫环”问题(点此跳转百科词条)
约瑟夫环(约瑟夫问题)是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。通常解决这类问题时我们把编号从0~n-1,最后 结果+1即为原问题的解。
代码
def standard_joseph(n, k, m):
''' 标准约瑟夫环:\n 约瑟夫环(约瑟夫问题)是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。通常解决这类问题时我们把编号从0~n-1,最后 结果+1即为原问题的解。 '''
persons = list(range(1, n+1)) # 列表1~n代表人的初始站队位置。
k += m-1 # 第一个淘汰的人的位置。
def resursive_cook(k, m):
''' 递归工作函数 '''
if persons == []: # 人全部淘汰,
return
if k <= len(persons):
print(persons.pop(k-1), end=', ')
k += m-1 # 下一个被淘汰的人位置。
else:
while k > (width := len(persons)):
k -= width
resursive_cook(k, m) # 递归调用。
resursive_cook(k, m)
mypycolor完整源码(源码较长,点此跳过源码)
#!/sur/bin/nve python
# coding: utf-8
'''
Author:梦幻精灵_cq
date:2022-10-27
'''
from time import localtime, time, sleep
# 打印颜色设置字符。
blue = '\033[34;5m'
red = '\033[91;5m'
green = '\033[92;5m'
gray = '\033[90m'
offall = '\033[0m'
def j(n):
'''用for循环解“约瑟夫环”一种变形问题。\n 约瑟夫环的一种变形。我们考虑的问题是开始时有n个人,记为1到n,站成一个圆圈。每一步,每第2个人将被去除,直到只剩下一个人为止。我们把剩下的人记为J(n),用程序求出1≤n≤16的J(n)。'''
persons = list(range(1, n+1))
k = [0] # 确定第一个被删除人的位置。
while len(set(persons)) > 2:
# print(persons) #调试用语句。
for i in range(len(persons)):
if len(set(persons)) == 2:
break
if k[0] != 0 and persons[i] != 0:
#print(persons[i], end=', ')
persons[i] = 0
k[0] = 0
else:
k[0] = 1
persons = list(set(persons))
if 0 in persons:
persons.remove(0)
# input(persons) # 调试用语句。
return persons[0]
def j_resursive(n, k=1, m=2):
''' 递归模板解析约瑟夫环的一种变形。\n 约瑟夫环的一种变形。我们考虑的问题是开始时有n个人,记为1到n,站成一个圆圈。每一步,每第2个人将被去除,直到只剩下一个人为止。我们把剩下的人记为J(n),用程序求出1≤n≤16的J(n)。'''
persons = list(range(1, n+1)) # 用1~n来设置n个人的最初站位。
k += m-1 # 第一个被删除人的位置
def resursive_cook(k, m):
''' 递归删除人 '''
while k <= len(persons):
print(persons.pop(k-1), end=', ')
k += m-1 # 从下一个人开始数数。
else:
k -= len(persons)
if len(persons) > 1: # 只剩下一个人,递归结束。
resursive_cook(k, m)
else:
return
resursive_cook(k, m) # 递归删除人。
#input(persons) # 调试用语句。
return persons[0] #返回最后剩下的人。
if __name__ == '__main__':
print(f"\n{gray}{j.__doc__}{offall}\n")
t0 = time()
for i in range(1, 17):
print('\n去除人位置顺序:', end='')
print(f"\n当队列为{blue}{i:2}{offall}人时,约瑟夫环最后剩下的是第{green}{j(i):2}{offall}人。")
print(f"\n{'':>17}循环用时{green}{time()-t0:2.6f}{offall}秒。")
y, M, d, h, m, s = localtime()[:6]
input(f"{'~'*14} {blue}{y}-{M:02}-{d:02}{offall} {green}{h:02}:{m:02}:{s:02}{offall} {'~'*15}")
def gapas_story(n=30, k=1, m=9):
'''数学家Gapas(加帕斯)讲的故事:\n 17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:\n 30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。'''
persons = list(range(1, n+1)) # 用1~n的数组表示30人的队列。
def resursive_work(k, m):
''' 递归算法工作函数。'''
if len(persons) == 15: # 终止递归。
return
k += m-1 # 非教徒位置计算。
while k > len(persons):
k -= len(persons) # while 循环处理大于列表长度的情况。
print(persons.pop(k-1), end=', ') # k 位置的人在列表中下标为 k-1 。
resursive_work(k, m) # 递归调用。
resursive_work(k, m) # 调用函数开始递推。
return(', '.join(map(str, persons))) # 返回教徒应处位置。
if __name__ == '__main__':
print(f"\n{gray}{standard_joseph.__doc__}{offall}\n\n{green}{' resursive 递归解 '.center(47,'~')}{offall}")
t0 = time()
print(f"\n{blue}非教徒下水顺序:{offall}")
print(f"\n\n{blue}教徒应处的位置:\n{green}{gapas_story()}{offall}\n")
print(f"\n{'':>14}程序耗时{green}{time()-t0:10.6f}{offall} 秒。")
y, M, d, h, m, s = localtime()[:6]
input(f"{'~'*14} {blue}{y}-{M:02}-{d:02}{offall} {green}{h:02}:{m:02}:{s:02}{offall} {'~'*15}")
def josephus_story(n=41, k=1, m=3):
''' Josephus的故事:\n 据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。\n 然而Josephus和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。\n 问题是,Josephus and his friend,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。'''
persons = list(range(1, n+1))
def eliminate(k, m):
''' 从第k人开始,步长为m淘汰人。'''
if len(persons) == 2:
return
k += m -1
while len(persons) < k:
k -= len(persons)
print(persons.pop(k-1), end=', ')
eliminate(k, m)
eliminate(k, m)
return persons
if __name__ == '__main__':
print(f"\n{gray}{josephus_story.__doc__}{offall}")
t0 = time()
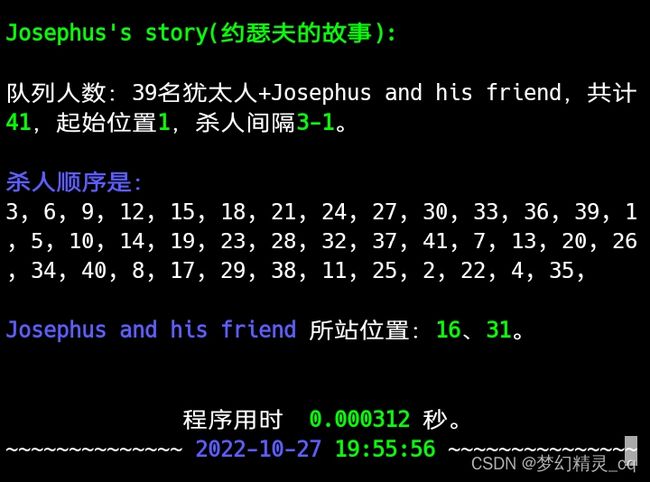
print(f"\n{green}Josephus's story(约瑟夫的故事): {offall}\n\n队列人数:39名犹太人+Josephus and his friend,共计{green}41{offall},起始位置{green}1{offall},杀人间隔{green}3-1{offall}。\n\n{blue}杀人顺序是:{offall}")
persons = josephus_story()
print(f"\n\n{blue}Josephus and his friend{offall} 所站位置:{green}{persons[0]}{offall}、{green}{persons[1]}{offall}。\n")
print(f"\n{'':>14}程序用时{green}{time()-t0:10.6f}{offall} 秒。")
y, M, d, h, m, s = localtime()[:6]
input(f"{'~'*14} {blue}{y}-{M:02}-{d:02}{offall} {green}{h:02}:{m:02}:{s:02}{offall} {'~'*15}")
def gapas_story(n=30, k=1, m=3):
'''数学家Gapas(加帕斯)讲的故事:\n 17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:\n 30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。'''
persons = list(range(1, n+1)) # 用1~n的数组表示30人的队列位置。
while len(persons) > 15:
k += m-1 # 定位非教徒。
while k > len(persons):
k -= len(persons) # while 处理 k 大于列表长度。
print(persons.pop(k-1), end=', ') # 推非教徒下水。
return ', '.join(map(str, persons)) # 返回教徒应处位置列表。
if __name__ == '__main__':
print(f"\n{gray}{gapas_story.__doc__}{offall}\n\n{green}{' While 循环解 '.center(47,'~')}{offall}")
t0 = time()
print(f"\n{blue}非教徒下水顺序:{offall}")
print(f"\n\n{blue}教徒应处的位置:\n{green}{gapas_story()}{offall}\n")
print(f"\n{'':>14}程序耗时{green}{time()-t0:10.6f}{offall} 秒。")
y, M, d, h, m, s = localtime()[:6]
input(f"{'~'*14} {blue}{y}-{M:02}-{d:02}{offall} {green}{h:02}:{m:02}:{s:02}{offall} {'~'*15}")
def standard_joseph(n, k, m):
''' 标准约瑟夫环:\n 约瑟夫环(约瑟夫问题)是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。通常解决这类问题时我们把编号从0~n-1,最后 结果+1即为原问题的解。 '''
persons = list(range(1, n+1)) # 列表1~n代表人的初始站队位置。
k += m-1 # 第一个淘汰的人的位置。
def resursive_cook(k, m):
''' 递归工作函数 '''
if persons == []: # 人全部淘汰,
return
if k <= len(persons):
print(persons.pop(k-1), end=', ')
k += m-1 # 下一个被淘汰的人位置。
else:
while k > (width := len(persons)):
k -= width
resursive_cook(k, m) # 递归调用。
resursive_cook(k, m)
if __name__ == '__main__':
print(f"\n{gray}{standard_joseph.__doc__}{offall}\n\n{green}{' 标准约瑟夫环 '.center(44,'~')}{offall}")
while True:
try:
n, k, m = map(int, input(f"{'':>8}{blue}输入({green}如 41 1 3{offall}):").split())
break
except Exception as error:
print(f"{red}{' 输入错误!':~^45}{offall}", end='\r')
sleep(0.3)
print(' '*50, end='\r')
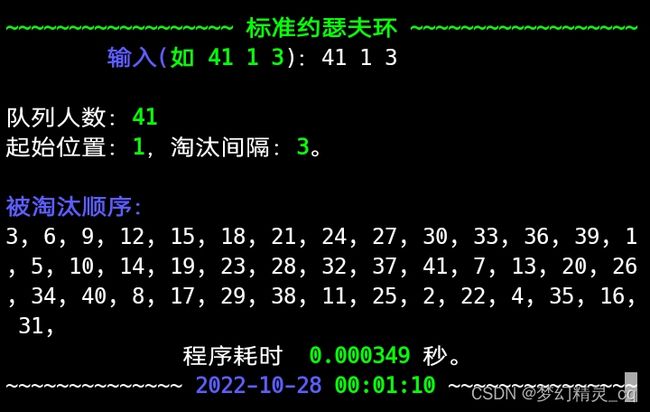
print(f"\n队列人数:{green}{n}{offall}\n起始位置:{green}{k}{offall},淘汰间隔:{green}{m}{offall}。")
t0 = time()
print(f"\n{blue}被淘汰顺序:{offall}")
standard_joseph(n, k, m)
print(f"\n{'':>14}程序耗时{green}{time()-t0:10.6f}{offall} 秒。")
y, M, d, h, m, s = localtime()[:6]
input(f"{'~'*14} {blue}{y}-{M:02}-{d:02}{offall} {green}{h:02}:{m:02}:{s:02}{offall} {'~'*15}")
__上一篇:__ “判断两个长度不同(数位不等)的整数能否顺序拼接成最大的一个整数”算法诞生记
__下一篇:__
我的HOT博:
- New:给定字符串提取姓名(字符串、list、re“零宽断言”)(1051阅读)
- New:我的 Python.color() (Python 色彩打印控制)(1125阅读)
- New:python清屏(1290阅读)
- 回车符、换行符和回车换行符(1322阅读)
- Linux 脚本文件第一行的特殊注释符(井号和感叹号组合)的含义(1171阅读)
- pandas 数据类型之 Series(1224阅读)
- 聊天消息敏感词屏蔽系统(字符串替换 str.replace(str1, *) )(1270阅读)
- 练习:银行复利计算(用 for 循环解一道初中小题)(1188阅读)
- pandas 数据类型之 DataFrame(2136阅读)
- :班里有人和我同生日难吗?(蒙特卡洛随机模拟法)(2180阅读)
- Python字符串居中显示(2359阅读)
- 练习:求偶数和、阈值分割和求差( list 对象的两个基础小题)(1665阅读)
- 用 pandas 解一道小题(2007阅读)
- 可迭代对象和四个函数(1083阅读)
- “快乐数”判断(1252阅读)
- 罗马数字转换器(构造元素取模)(2159阅读)
- Hot:罗马数字(转换器|罗生成器)(4750阅读)
- Hot:让QQ群昵称色变的代码(36654阅读)
- Hot:斐波那契数列(递归| for )(4071阅读)
- 柱状图中最大矩形(1663阅读)
- 排序数组元素的重复起止(1258阅读)
- 电话拨号键盘字母组合(1402阅读)
- 密码强度检测器(1986阅读)
- 求列表平衡点(1837阅读)
- Hot: 字符串统计(4308阅读)
- Hot:尼姆游戏(聪明版首发)(3493阅读)尼姆游戏(优化版)(1175阅读)
推荐条件 点阅破千
回目录

精品文章:
- 好文力荐:《python 完全自学教程》齐伟书稿免费连载
- OPP三大特性:封装中的property
- 通过内置对象理解python'
- 正则表达式
- python中“*”的作用
- Python 完全自学手册
- 海象运算符
- Python中的 `!=`与`is not`不同
- 学习编程的正确方法
来源:老齐教室
回目录
Python 入门指南【Python 3.6.3】
好文力荐:
-
全栈领域优质创作者——寒佬(还是国内某高校学生)好文:《非技术文—关于英语和如何正确的提问》,“英语”和“会提问”是学习的两大利器。
-
【8大编程语言的适用领域】先别着急选语言学编程,先看它们能干嘛
-
靠谱程序员的好习惯
CSDN实用技巧博文:
- 8个好用到爆的Python实用技巧
- python忽略警告
- Python代码编写规范
- Python的docstring规范(说明文档的规范写法)