机器学习第七章之K近邻算法

当有多种类别数据时，我们常常面临着将新加入的数据进行分门别类的问题。比如根据口味色泽划分新的葡萄酒的类别，根据内容形式划分新上映电影的类别，根据过往人脸特征进行人脸识别。我们可以采用机器学习中非常经典的K近邻算法来解决这些问题，这一章节将讲解K近邻分类算法的原理和代码实现，同时将介绍手写数字识别模型的案例来巩固所学知识点。

7.1 K近邻算法

K近邻算法 (K-Nearest Neighbor, 也简称KNN算法) 是非常经典的机器学习算法，这一节主要介绍一下K近邻算法的基本原理，并通过简单案例来讲解如何通过Python来实现K近邻算法。

7.1.1 K近邻算法的原理介绍

K近邻算法的原理非常简单：对于一个新的数据而言，K近邻算法的目的就是在已有数据中寻找与它最相似的K个数据，或者说“离它最近”的K个数据，如果这K个点大多数属于某一个类别，则该样本也属于这个类别。

以上图为例，假设五角星和三角形分别代表两类不同的电影，一类是爱情片，一类是动作片。此时加入一个新样本正方形，此时需要判断该电影的类别。当选择以离新样本最近的3个近邻点时(K=3)为判断依据时，这3个点由1个五角星和2个三角形组成，由少数服从多数原则，可以认为新样本属于三角形的类别，即新样本是一部动作片。同理，当选择离新样本最近的5个近邻点时(K=5)为判断依据时，离新样本最近的5个点由3个五角星和2个三角形组成，由少数服从多数原则，认为新样本属于五角星的类别，即新样本是一部爱情片。
明白了K的含义后，我们来解释下如何来判断两个数据的相似度，或者说两个数据的距离，这里采用最为常见欧氏距离来定义向量空间内2个点的距离，对于二维空间而言，样本A的两个特征值为(X1,Y1)，而样本B的两个特征值为(X2,Y2)，那么两个样本的距离公式如下：

这个其实就是常见的两点间距离公式，如下图所示，其适合于特征变量只有两个的情况下。

实际应用中，数据的特征通常有n个，此时可将该距离公式推广到n维空间，如n维向量空间下A点坐标为(X1,X2,X3,…Xn)，B点坐标为(Y1,Y2,Y3,…,Yn)，那么A、B两点间的欧氏距离为：

7.1.2 K近邻算法的计算步骤及代码实现

在讲解如何利用代码实现之前，我们先用一个简单的数学案例讲解下kNN算法的步骤。
1.读取数据
这里以一个简单的例子来讲解一下K近邻算法的基本原理：如何判断葡萄酒的种类。为方便演示，我们只选取了2个特征变量来对葡萄酒进行分类，实际生活中，用来评判葡萄酒的指标要多得多。此处假设可以根据酒精含量和苹果酸含量将葡萄酒分为2类。

import pandas as pd
df = pd.read_excel('葡萄酒.xlsx')

此时的df如下表所示，为方便演示，该数据集只有5个原始样本数据。

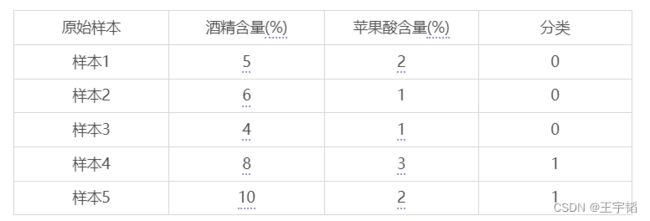
其中酒精含量代表葡萄酒中酒精的含量高低，苹果酸含量代表葡萄酒中苹果酸的含量高低，分类取值为0代表葡萄酒A，分类取值为1代表葡萄酒B。
现在需要使用K近邻算法对一个新样本进行分类，该新样本的特征数据如下所示，那么这个新样本是属于葡萄酒A呢，还是属于葡萄酒B呢？

2.计算距离
此时我们可以利用距离公式来计算新样本与已有样本之间的距离，也即不同样本间的相似度，例如我们可以计算新样本与样本1的距离，公式如下：

同理可以计算新样本与其他原始样本的距离，如下表所示：

3.根据K值判定类别
获得了各个原始样本与新样本的距离后，我们就可以将其根据距离由近到远进行排序，如下表所示：

此时如果令K值等于1，也就是以离新样本距离最近的原始样本的种类作为新样本的种类，那么新样本离样本2最近，那么新样本的分类为0，也就是葡萄酒A。
如果令K值等于2，虽然有两个分类，但是它会优先选择2个分类结果中离它最近的那个。
如果令K值等于3，那么就是以离新样本最近的3个原始样本的多数样本的种类为判断依据，此时最近的3个原始样本是样本2、样本1、样本4，它们中以分类0居多，所以判定新样本的分类为0，也就是葡萄酒A。

4.K近邻算法的代码实现
上面讲解了K近邻算法基本运算步骤，而其实这些运算步骤在Python中已经有相关的库给封装好了，直接进行调用即可。
首先把原始数据进行特征变量和目标变量的切分从而方便之后进行模型的训练，代码如下：

X_train = df[['酒精含量(%)','苹果酸含量(%)']]
y_train = df['分类']  

然后就可以直接调用Python已经开发好的相关库来进行K进邻算法的运算了，代码如下：

from sklearn.neighbors import KNeighborsClassifier as KNN
knn = KNN(n_neighbors=3)  
knn.fit(X_train, y_train)

其中第一行代码为引用的Scikit-Learn库中的KNN模型；第二行代码设置KNN模型中的临近参数n_neighbors，也就是上面提到过的K值，这里设置其值为3，也就选取最近的三个样本，如果不设置的话则取默认值5；第三行代码就是进行模型训练了。
模型训练完之后就可以来进行预测了，代码如下：

X_test = [[7, 1]]  # X_test为测试集特征变量
answer = knn.predict(X_test)  

第一行代码中的X_test就是新样本的特征变量：7%的酒精含量及1%的苹果酸含量，注意这里要写成二维数组的形式，不然模型会报错；第二行就是对目标变量进行预测了，得到的是一个一维数组，此时得到的预测结果answer如下所示，和之前通过数学运算的方法获得结果一致。

[0]

感兴趣的读者可以在测试数据中再传入一个新样本，比如我们传入一个和样本4（类别1）一样的样本（8%的酒精度，3%的苹果酸含量），代码如下：

X_test = [[7, 1], [8, 3]]  # 这里能帮助理解为什么要写成二维数组的样式
answer = knn.predict(X_test)  

此时得到的预测结果answer如下所示，可以看到第二个和样本4一样的新样本的确被预测为和样本4一样的类别，也即类别1了。

[0 1]

补充知识点：K近邻算法回归模型
K近邻算法除了可以做分类分析，也可以做回归分析，分别对应的模型为K近邻算法分类模型（KNeighborsClassifier）及K近邻算法回归模型（KNeighborsRegressor）。
KNeighborsClassifier将待预测样本点最近邻的k个训练样本点中出现次数最多的分类作为待预测样本点的分类；
KNeighborsRegressor将待预测样本点最近邻的k个训练样本点的平均值作为待预测样本点的回归值。
K近邻算法回归模型的引入方式：

from sklearn.neighbors import KNeighborsRegressor

在Jupyter Notebook编辑器中，在引入该库后，可以通过如下代码获取官方讲解内容：

KNeighborsRegressor?

K近邻算法回归模型简单代码演示如下所示：

from sklearn.neighbors import KNeighborsRegressor
X = [[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]]
y = [1, 2, 3, 4, 5]

model = KNeighborsRegressor(n_neighbors=2)
model.fit(X, y)

print(model.predict([[5, 5]]))

其中X是特征变量，其共有2个特征；y是目标变量；第5行引入模型，并设置超参数n_neighbors(K值)为2；第6行通过fit()函数训练模型；最后1行通过predict()函数进行预测，预测结果如下：

[2.5]

7.2 数据预处理之数据归一化

这一节主要讲解一个数据预处理的一个技巧：数据归一化（也称数据标准化）。数据归一化的目的是为了消除不同特征变量量纲相差较大的影响。例如下表所示，我们把上节的酒精含量都放大10倍仅作教学演示，苹果酸含量保持不变，此时两者的量纲级别相差就较大了。

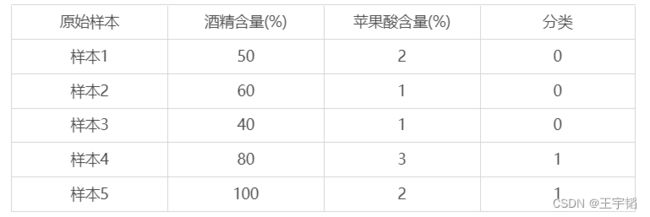
此时如果直接使用K近邻算法来进行建模，那么酒精含量在模型中的重要性将远远超过苹果酸的含量，这样会丧失苹果酸含量这一特征变量的作用，而且结果也会有较大误差。举例说明，对于一个新的样本，其酒精含量为70%，苹果酸含量为1%，此时它与样本1的距离公式为：

可以看到此时的距离几乎就是由酒精含量主导，苹果酸含量由于量纲相差较大，几乎不发挥作用，那么此时如果不进行数据数据预处理，会导致预测结果有失偏颇。
因此当不同特征变量之间量纲相差较大且在建模时相互影响的时候，我们通常会对数据进行预处理，这里的手段叫作数据归一化。常见的数据归一化的方法有min-max标准化(也称离差标准化)以及Z-score标准化(也称均值归一化)。

7.2.1 min-max标准化

min-max标准化（Min-Max Normalization）也称离差标准化，它利用原始数据的最大最小值把原始数据转换到[0,1]区间内，转换函数如下：

其中x、分别为转换前、后的值，max、min分别为样本的最大值和最小值。
例如一个样本集中最大值为100，最小值为40，此时x为50，那么归一化后的值如下所示：

还是以之前的葡萄酒的案例为例，我们来对它里面的数据进行归一化处理。

import pandas as pd
df = pd.read_excel('葡萄酒2.xlsx')
X = df[['酒精含量(%)','苹果酸含量(%)']]
y = df['分类']

这里只需要对特征变量X进行归一化处理，目标变量y无需处理，在Python中可以直接调用min-max标准化的相关模块，代码如下：

from sklearn.preprocessing import MinMaxScaler
X_new = MinMaxScaler().fit_transform(X)

其中第一行引入相关模块：MinMaxScaler；第二行通过fit_transform()函数对原始数据进行归一化转换。此时数据归一化后的特征变量X_new如下所示：

[[0.16666667 0.5       ]
 [0.33333333 0.        ]
 [0.         0.        ]
 [0.66666667 1.        ]
 [1.         0.5       ]]

其中第一列为酒精含量归一化后的值，第二列为苹果酸含量归一化后的值，可以看到它们都属于[0,1]了。在实际应用中，通常将所有数据都归一化后，再进行训练集和测试集划分。

7.2.2 Z-score标准化

Z-score标准化(mean normaliztion)也称均值归一化，通过原始数据的均值（mean）和标准差（standard deviation）对数据进行归一化。归一化后的数据符合标准正态分布，即均值为0，标准差为1。转化函数为：

其中x、分别为转换前、后的值，mean为原数据的均值，std为原数据的标准差。
同样在Python中有现成的模块可以对数据进行均值归一化处理，代码如下：

from sklearn.preprocessing import StandardScaler
X_new = StandardScaler().fit_transform(X)

其中第一行引入相关模块：StandardScaler；第二行通过fit_transform()函数对原始数据进行归一化转换。此时数据归一化后的特征变量X_new如下所示：

[[-0.74278135  0.26726124]
 [-0.27854301 -1.06904497]
 [-1.2070197  -1.06904497]
 [ 0.64993368  1.60356745]
 [ 1.57841037  0.26726124]]

其中第一列为酒精含量均值归一化后的值，第二列为苹果酸含量均值归一化后的值，此时它们均值为0，标准差为1的正太分布。
总结来说，数据归一化的代码并不复杂，仅仅2-3行的代码就能帮忙避免很多问题，因此对于一些量纲相差较大的特征变量，实战中通常先进行数据归一化后再进行训练集和测试集划分。
除了K近邻算法模型，还有些模型也是基于距离的，所以量纲对模型影响较大，就需要归一化数据，例如支持向量机模型、K-means聚类分析，PCA主成分分析等。此外对于一些线性模型，例如第三章的线性回归模型和第四章的逻辑回归模型有时也需要进行数据归一化处理。
注意对于树模型而言，则无需做归一化处理，因为数值缩放不影响分裂点位置，对树模型的结构不造成影响。因此决策树模型，以及基于决策树模型的随机森林模型、Adaboost模型、GBDT模型、Xgboost模型、LightGBM模）通常都不需要进行数据归一化处理，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率。
其实有时如果你不知道是否要做归一化，那么可以归一化试试看（也就2、3行代码的事），看看模型预测准确度是否有提升，如果提升较明显的话则推荐使用归一化处理方式，笔者验证过（10.3.4小节补充知识点有演示），在树模型相关的机器学习模型中，进行数据归一化对预测结果不会产生影响。

7.3 案例实战 - 手写数字识别模型

这一节我们将以一个较为经典的手写数字识别模型来讲解如何在实战中应用K近邻算法。

7.3.1 案例背景

图像识别是机器学习领域一个非常重要的应用场景，像现在非常火的人脸识别就是基于机器学习的相关算法，这里首先介绍一个较为简单的图像识别的案例：手写数字识别模型，在之后的章节讲解完PCA主成分分析后，我们将再介绍人脸识别的代码实现，两者的原理其实都有共通之处，所以这里学完手写数字识别模型后，会对人脸识别也会有个初步的了解。

7.3.2 手写数字识别原理

手写数字识别的本质就是把如下图所示的手写数字图片转换成计算机能够处理的数字。

1.图像二值化
如下图所示，我们将图片格式的数字4转换成由0和1组成的“新的数字4”了。这是一个32x32大小的矩阵，数字1代表有颜色的地方，数字0代表无颜色的地方，这样就完成了手写数字识别的最关键的第一步：将图片转为计算机能识别的内容：数字0和1，这个也叫作图像二值化。

备注：关于如何实现这样图像二值化的效果，将在这一节补充知识点进行讲解。

2.二维数组转换为一维数组
经过图像二值化的处理之后，我们获得了一个二维的数组(32x32的0-1矩阵)，为了方便进行机器学习建模，还需要对这个二维数组进行一个简单处理：在上图二维数组中，第一行之后依次拼接第二行的32个数字，第三行的32个数字……直至第32行的32个数字，这时候便得到一个1x1024的一维数组，如下所示：

这样便把一个图片格式的数字4转换成一个有1024个元素的一维数组格式了，对于不同的数字我们也可以进行类似的处理。对于这样的一维数组格式，就可以计算不同手写数字之间的距离，或者说这些手写数字的相似度了，从而进行手写字体识别了。
备注：关于如何将32x32的二维数组转换成1x1024的一维数组可以参考本节补充知识点。

3.距离计算
手写数字图片处理后形成了32x32的0-1矩阵，将32x32的矩阵变形为1x1024的行向量后，两张图片所对应的行向量间的欧氏距离可以反映两张图片的相似度。因此我们可以利用K近邻算法模型计算新样本与原始训练集中各个样本的欧氏距离，取新样本的k个近邻点，并以大多数近邻点所在的类别作为新样本的分类。
举个例子，对于一个样本手写数字4，它转换成如下的1x1024的行向量：

对于另一个手写数字x，其转换后的1x1024行向量如下，假设其只有中间的一个数字不同：

那么手写数字x与样本手写数字4的距离就如下所示：

利用类似的原理，对于一个新样本，我们可以计算它与每个不同样本数字之间的距离，从而根据与其距离最近的k个临近点判别其属于哪个类别，即哪个数字。

7.3.3 手写数字识别编程实现

根据上面的识别原理，这里的数据集为1934个处理好的手写数字0-9的1x1024矩阵。如下图所示，其中每一行对应一个手写数字，第一列“对应数字”为对应的手写数字，其余每一列为该手写数字对应的1x1024矩阵中的每一个数字。

1.读取数据
首先通过pandas库读取数据，代码如下：

import pandas as pd
df = pd.read_excel('手写字体识别.xlsx')

此时获取数据前5行如下所示：

其中第一列“对应数字”为目标变量y，其余1024列为特征变量X，我们的目的就是利用这些数据，搭建手写数字识别模型。

2.提取特征变量和目标变量
通过如下代码将特征变量和目标变量单独提取出来，代码如下：

X = df.drop(columns='对应数字') 
y = df['对应数字']  

这里通过drop()函数删除“对应数字”这一列，将剩下的数据作为特征变量赋值给变量X。然后通过提取“对应数字”这一列作为目标变量y。
这里所有样本的1x1024矩阵元素都由0，1构成，所以不需要再归一化处理样本数据。如果在其他场景下中出现数量级相差较大的特征变量，便还需要对数据进行归一化处理，如下所示：

from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)

3.划分训练集和测试集
通过和之前章节类似的代码划分训练集和测试集数据：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)

这里的test_size选择为0.2，也即20%的数据划分为测试集数据。random_state的数字123没有特殊含义，可以换成别的数字，它只是相当于一个种子参数，使得这样每次划分数据的时候，划分的训练集和测试集内容都是一致的。

4.模型搭建
划分完训练集和测试集数据后，我们使用K近邻算法分类器进行模型搭建，代码如下：

from sklearn.neighbors import KNeighborsClassifier as KNN
knn = KNN(n_neighbors=5) 
knn.fit(X_train, y_train)

第一行代码从Scikit-Learn库引入K近邻分类器（KNeighborsClassifier），并简写为KNN。
第二行代码将KNN分类器赋值给knn变量，并设置n_neighbors为默认值5，表示k近邻算法中选择5个近邻点来决定新样本的分类。
第三行代码通过fit()方法来进行模型的训练，其中传入的参数正是上一步骤所获得的训练集数据X_train,y_train。

5.模型预测 - 预测数据结果
通过如下代码即可预测测试集数据。

y_pred = knn.predict(X_test)

预测的y_pred如下所示，这里通过print(y_pred[0:100])打印了前100个预测数据：

通过和之前章节类似的代码，我们可以将预测值和实际值进行对比：

a = pd.DataFrame()  # 创建一个空DataFrame 
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)

将此时的a打印输出如下：

此时前5组数据的预测准确度为100%，通过如下代码可以查看所有测试集的预测准确度：

from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)

此时获得的模型准确度评分score为0.979，也就是说模型的预测准确度达到了97.9%。
除了用accuracy_score()函数来获取模型评分外，其实Scikit-Learn库的K近邻分类器自带模型评分功能，代码如下：

score = knn.score(X_test, y_test)

这里的knn为上面训练好的模型，它会自动根据X_test的值计算出预测值去和真实值进行比对，从而获得预测准确度评分，这里同样可以得到评分score为0.979。
如果想进行参数调优，如上面采取的参数n_neighbors为默认值5，如果想看换成别的数是否更优，可以模仿之前讲解决策树模型时候的交叉验证和网格搜索来进行参数调优，代码如下：

from sklearn.model_selection import GridSearchCV
parameters = {'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8]}  # 候选参数
knn = KNN()
grid_search = GridSearchCV(knn, parameters, cv=5)  # 5折交叉验证
grid_search.fit(X_train, y_train)  # 以准确度为基础进行网格搜索，寻找最优参数
grid_search.best_params_['n_neighbors']  # 获取最优参数

7.3.4 补充知识点：图像识别原理详解

对于计算机而言 ，它是没有办法直接识别一张图片的，我们需要通过一些预处理的手段把图片转换成计算机能够识别的内容，比如说数字0和1。这里便来讲解Python如何来把一张图片进行简单处理变成计算机可以识别的内容。

1.图片大小调整及显示
第三方图像处理库Pillow库是Python一款功能强大的图像处理库，简单好用，使用人数众多，如果没有该库的话，可以通过“pip install pillow”进行安装，简单演示代码如下：

from PIL import Image
img = Image.open('数字4.png')
img = img.resize((32,32))
img.show()

我们首先从引入Pillow库中的Image模块来处理图像。其中open()函数可以打开后缀为jpg，png等的图片；resize()函数可以调整图像大小，这里调整为32*32像素的数字4；show()函数可以显示图片，结果如下：

2.图片灰度处理
此时获得的是一个彩色的数字4，我们需要对其进行灰度处理，将其变成黑白颜色，方便之后好将其转换成数字0和1，代码如下：

img = img.convert('L')

其中代码img.convert(‘L’)是对原图进行灰度处理，显示结果如下：

3.图片二值化处理
获得黑白颜色的数字4后，下面就是关键的图像二值化处理了，代码如下：

import numpy as np
img_new = img.point(lambda x: 0 if x > 128 else 1)
arr = np.array(img_new)

第一行代码引入numpy库为之后的将图像转为二维数组做准备；
第二行代码中point()函数可以操控每一个像素点，point()函数中传入的内容为之前讲pandas库时讲过的lambda匿名函数，其含义为对色彩数值大于128的像素点赋值为0，反之赋值为1。这是因为图像在进行灰度处理后，色彩由0-255的数字表示，其中0代表黑色，255代表白色，所以这里以128为阈值进行划分，即原来偏白色的区域赋值为0，原来偏黑色的区域赋值为1。这样我们便完成了将颜色转换成数字的工作了。
第三行代码通过numpy.array()函数将刚刚已经转成数字的3232像素的图片转为32行32列的二维数组，并赋值给变量arr。
此时可以直接将arr通过print()函数打印出来，不过因为其行列较多，可能显示不全，所以我们通过如下代码打印它的每一行，其中arr.shape反映的是数组的行数和列数，arr.shape[0]表示行数(arr.shape[1]则表示列数)，这样通过for循环就可以打印每行内容了。

for i in range(arr.shape[0]):
    print(arr[i])

显示结果如下，可以看到此时的数字4就是由0和1两个数字组成的了。

4.二维数组转一维数组
上面获得的是一个3232的二维数组，还不利于数据建模，所以我们还需要通过reshape(1, -1)方法将其转换成一行(若reshape(-1,1)则转为一列），也即11024的一维数组，代码如下：

arr_new = arr.reshape(1, -1)

此时便实现了将一个彩色图片转换成如下的一维数组了：

我们可以打印arr_new或通过arr_new.shape查看此时的数据行列数，代码如下：

print(arr_new.shape)

结果如下，显示的的确是1行，1024列。

(1, 1024)

此时我们可以把这个处理过的图片“数字4”传入到我们上面训练好的knn模型中，代码如下：

answer = knn.predict(arr_new) 
print('图片中的数字为：' + str(answer[0]))

因为获取到answer是一个一维数组（类似列表），所以通过answer[0]提取其中的元素，因为数字不能进行字符串拼接，所以这里通过str()函数转换后进行字符串拼接，运行结果如下，结果的确预测为数字4。

图片中的数字为：4

了解了这些内容后便可以做一个有趣的实验了，我们可以用粗一点的笔手写一个数字，然后拍照，传入到如下代码23行的图片上传位置，亲自试试我们之前模型。这里汇总下完整代码：

# 主要分为三步，第一步训练模型，第二步处理图片，第三步导入模型并预测
# 1.训练模型
# 1.1 读取数据
import pandas as pd
df = pd.read_excel('手写字体识别.xlsx')

# 1.2 提取特征变量和目标变量
X = df.drop(columns='对应数字') 
y = df['对应数字']   

# 1.3 划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)

# 1.4 训练模型
from sklearn.neighbors import KNeighborsClassifier as KNN
knn = KNN(n_neighbors=5) 
knn.fit(X_train, y_train)  # 自此手写字体识别模型便搭建好了

# 2.处理图片
# 2.1 图片读取 & 大小调整 & 灰度处理
from PIL import Image
img = Image.open('测试图片.png')  # 这里传入手写的图片，注意写对文件路径
img = img.resize((32,32))
img = img.convert('L')

# 2.2 图片二值化处理 & 二维数据转一维数据
import numpy as np
img_new = img.point(lambda x: 0 if x > 128 else 1)
arr = np.array(img_new)
arr_new = arr.reshape(1, -1)

# 3.预测手写数字
answer = knn.predict(arr_new) 
print('图片中的数字为：' + str(answer[0]))

这里第23行代码用的测试图片如下所示：

最终获得的结果如下所示，与实际相符。

图片中的数字为：1

总体来说，K近邻算法是一个非常经典的机器学习算法，其原理清晰简单，容易理解，不过它也有些缺点，比如样本量较大时，计算量大，拟合速度较慢。而本章学习的手写数字识别模型其实也是图像识别模型中的一个简单应用，是为之后更精彩的图像识别模型打好基础。

点击下载。

7.4课程相关资源

笔者获取方式：微信号获取

添加如下微信：huaxz001 。

笔者网站：www.huaxiaozhi.com

王宇韬相关课程可通过：
京东链接：[https://search.jd.com/Search?keyword=王宇韬]，搜索“王宇韬”，在淘宝、当当也可购买。加入学习交流群，可以添加如下微信：huaxz001（请注明缘由）。

各类课程可在网易云、51CTO搜索王宇韬，进行查看。