求解车辆路径问题的强化学习方法
1 文章信息
《Reinforcement Learning for Solving the Vehicle Routing Problem》是32nd Conference on Neural Information Processing Systems (NeurIPS 2018)上的一篇文章。
2 摘要
我们提出了一种利用强化学习方法解决车辆路径问题(VRP)的端到端框架。在这种方法中,我们训练一个单一的模型,它仅通过观察奖励信号和遵循可行性规则,为从给定分布中采样的问题实例找到接近最优的解决方案。我们的模型表现为一个参数化的随机策略,通过应用策略梯度算法优化其参数,训练过的模型实时生成一系列连续动作的解,而不需要为每个新问题实例重新训练。在容量限制VRP上,我们的方法在中等规模问题实例的求解质量上优于经典的启发式和谷歌的OR-Tools,且计算时间相当(经过训练后)。我们将演示我们的方法如何处理分批交货的问题,并探讨这种交付对解决方案质量的影响。我们提出的框架可以应用于VRP的其他变体,如随机VRP,并有潜力更广泛地应用于组合优化问题。
3 介绍
车辆路径问题(VRP)是应用数学和计算机科学中研究了几十年的组合优化问题。VRP是一个计算困难的问题,许多精确和启发式算法已经被提出,但提供快速和可靠的解仍然是一项具有挑战性的任务。在VRP的最简单形式中,一辆容量有限的车辆负责向多个客户节点运送物品;当物品送完时,它必须返回仓库去取其他的物品。目标是优化一组路线,所有的起点和终点都在一个给定的节点(称为仓库),以获得可能的最大奖励,奖励通常是车辆总距离或平均服务时间的负数。即使只有几百个客户节点,这个问题在计算上也很难得到最优解。
在这项工作中,我们开发了一个框架,具有使用强化学习解决各种组合优化问题的能力,并展示如何应用它来解决VRP。为此,我们考虑问题的马尔可夫决策过程(MDP)的表述,其中最优解可以被视为一系列决策。
我们不是专注于为每个问题实例训练一个单独的模型,而是提出了一个结构,它可以很好地处理从给定分布中采样的任何问题。这意味着,如果我们生成一个新的VRP实例,该实例具有与我们在训练期间使用的相同的节点数量和车辆容量,以及相同的位置和需求分布,那么经过训练的策略将很好地工作,我们可以立即解决问题,而无需为每个新实例重新训练。只要我们逼近问题的生成分布,这个框架就可以被应用。可以将训练过的模型视为一个黑盒启发式(或元算法),它在合理的时间内生成高质量的解。
我们的模型由一个循环神经网络(RNN)解码器和一个注意力机制组成。在每个时间步中,静态元素的嵌入作为RNN解码器的输入,RNN的输出和动态元素的嵌入被送到一个注意力机制中,该注意力机制在下一个决策点可选择的可行目的地上形成分布。
4 模型
在本节中,我们正式定义了具有给定输入集合X={xi, i=1,…,M}的一般组合优化问题的问题和我们提出的框架。我们允许每个输入的某些元素在解码步骤之间更改,事实上,在许多问题中,例如VRP,就是这样的情况。动态元素可能是解码过程本身的工件,也可能是由环境强加的。例如,在VRP中,随着车辆访问客户节点,其余的客户需求会随时间变化;或者,我们可以考虑一个变量,即新客户的到来或随着时间的推移调整他们的需求值,这与车辆决策无关。形式上,我们用一系列元组{xit= (si, dit), t=0,1,…}来表示每个输入xi,其中si和dit分别是输入的静态和动态元素,它们本身也可以是元组。我们可以将xit看作描述时间t时输入i状态的特征向量。例如,在VRP中,xit给出了客户i的概况,其中si对应于客户i位置的二维坐标,dit是其在时间t时的需求。我们将用Xt表示固定时间t时所有输入状态的集合。
我们从任意输入X0开始,用指针y0指向该输入。在每个解码时间t (t=0,1,…)处,yt+1指向其中一个可用输入Xt,它决定了解码器下一步的输入;此过程将继续进行,直到满足终止条件。终止条件是问题特定的,表明所生成序列满足可行性约束。例如,在本文考虑的VRP中,终止条件是没有更多的需求需要满足。这个过程将生成一个长度为T的序列,Y={yt, T=0,…, T},可能有与输入长度M不同的序列长度。这是由于,例如,车辆可能需要多次返回仓库补充物品。我们还使用符号Yt表示到t时刻的解码序列,即Yt={y0,…,yt}。我们感兴趣的是找到一个随机策略π,它生成的序列Y在满足问题约束的同时,使损失目标最小化。最优策略π*生成最优解的概率为1。我们的目标是使π尽可能接近π*。与Sutskever类似,我们使用概率链式法则将序列Y产生的概率P (Y |X0)分解,如下所示:
是用状态转移函数f对问题表示进行递归更新。(1)右侧的每一个分量都通过注意力机制计算,即
![]()
其中g是一个输出输入大小的向量的仿射函数,ht是RNN解码器的状态,它汇总了之前解码步骤y0,…,yt的信息。
注释1:该模型既可以处理经典静态环境中的组合优化问题,也可以处理动态变化环境中的组合优化问题。在静态组合优化中,X0完全定义了我们要解决的问题。例如,在VRP中,X0包括所有客户位置以及他们的需求,以及仓库位置;然后,根据车辆目的地及其负载更新剩余的需求。考虑到这一点,通常存在一个定义良好的马尔可夫转移函数f,如(2)所定义,它足以更新决策点之间的动态。然而,我们的模型也可以应用于状态转移函数未知和/或受外部噪声影响的问题,因为训练没有明确地使用转移函数。然而,知道这个转换函数有助于模拟训练算法与之交互的环境。
4.1 指针网络的局限性
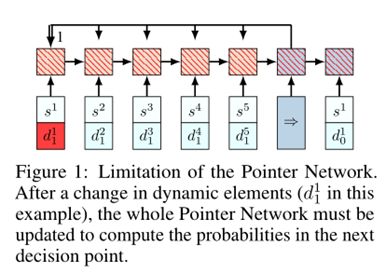
虽然Bello等人提出的框架在诸如背包问题和TSP等问题上工作良好,但它不适用于系统表示随时间变化的更复杂的组合优化问题,如VRP。Bello等人向RNN编码器输入一个随机序列。图1用一个例子说明了为什么在编码器中使用RNN是有限制的。假设在第一个决策步骤,该策略将车辆发送给客户1,其需求得到满足,即d10≠d11。然后在第二个决策步骤中,我们需要使用新的d11信息重新计算整个网络,以选择下一个客户。动态元素使网络的转发变得复杂,因为当输入发生变化时,编码器/解码器应该进行更新。在反向传播积累梯度的过程中,情况更加糟糕,因为我们需要记住动态元素什么时候发生了变化。为了解决这个问题,我们要求模型对输入序列保持不变,以便改变任意两个输入的顺序都不会影响网络。
4.2 提出的神经网络模型
我们认为RNN编码器为编码器增加了额外的复杂性,但实际上不是必要的,通过省略它可以使该方法更加通用。只有当输入传递顺序信息时才需要RNN;例如,在文本翻译中,为了使译文准确,必须捕捉词语的组合及其相对位置。但这里的问题是,当输入集中没有有意义的顺序时,为什么我们需要在编码器中有它们来解决组合优化问题?例如,在VRP中,输入是一组具有各自需求的无序客户位置,其顺序没有意义;任何随机排列都包含与原始输入相同的信息。因此,在我们的模型中,我们简单地忽略了编码器RNN,直接使用嵌入的输入而不是RNN的隐藏状态。通过这种修改,许多计算的复杂性消失了,而不降低模型的效率。
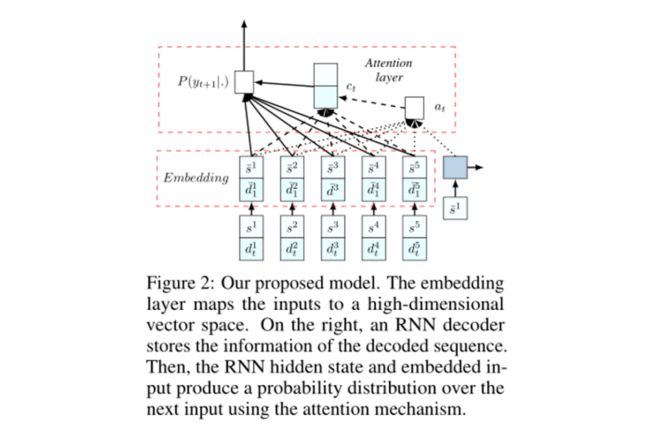
如图2所示,我们的模型主要由两个部分组成。第一个是一组将输入映射到D维向量空间的嵌入。我们可能有多个嵌入对应于输入的不同元素,但它们在输入之间是共享的。我们模型的第二个部分是一个解码器,它在每个解码步骤都指向一个输入。我们使用RNN对解码器网络进行建模。注意,我们只将静态元素作为输入提供给解码器网络。动态元素也可以作为解码器的输入,但我们在VRP上的实验并没有表明这样做有任何改进,所以动态元素只在注意层中使用,接下来将介绍。
4.3 注意力机制
注意力机制是一种可微结构,用于寻址输入的不同部分。图2说明了我们方法中使用的注意力机制。在解码器的第i步,我们利用一个基于上下文的注意力机制,它使用一个可变长度的对齐向量at从输入中提取相关信息。at指定每个输入数据点在接下来的解码步骤t中可能有多大的相关性。
设xit¯=(si¯, dit¯)为嵌入的输入i,ht∈RD为解码第t步时RNN单元的内存状态,则计算对齐向量at为
![]()
这里的“;”表示两个向量的拼接。我们通过结合上下文向量ct计算条件概率,计算为
用嵌入式输入,然后用softmax函数将值归一化,如下所示
![]()
在(4)-(6)中,va、vc、Wa和Wc是可训练变量。
4.4 训练方法
为了训练网络,我们使用了众所周知的策略梯度方法。为了使用这些方法,我们用参数θ来参数化随机策略π。策略梯度方法使用相对于策略参数的期望回报梯度的估计来迭代改进策略。原则上,策略梯度算法包含两个网络:(i)预测在任何给定决策步骤下一个行动的概率分布的actor网络,(ii)估计来自给定状态的任何问题实例的奖励的critic网络。
让我们考虑一组用M表示的问题,以及它们的概率分布,用ΦM表示。在训练过程中,根据分布ΦM生成问题实例。我们还在推理中使用相同的分布来生成测试示例。
使用REINFORCE算法求解VRP 算法3对REINFORCE算法进行了总结。我们有两个分别与actor和critic相关的权重向量为θ和φ的神经网络。我们从M中抽取N个样本问题,用蒙特卡罗模拟得到了关于当前策略πθ的可行序列。我们采用上标n来表示第n个实例的变量。在所有N个问题的解码终止后,我们在步骤14中计算相应的奖励和策略梯度来更新行动者网络。在这一步中,V (Xn0;φ)为实例问题n的奖励近似,使用critic网络中计算。我们还在第15步中更新了critic网络,以减少期望奖励与蒙特卡洛转出过程中观测奖励之间的差异。
5 数值实验
我们的数值实验表明,我们的框架比为VRP设计的著名的经典启发式算法的性能要好得多,而且在最差结果仍然相对接近最优结果的意义上,它是鲁棒的。将我们的方法与OR-Tools VRP引擎 (这是最好的开源VRP求解器之一)进行比较,我们观察到一个显著的改进;在拥有50和100个客户点的VRP实例中,我们的方法在大约61%的实例中提供了更短的行程。我们在这项研究中观察到的另一个有趣的现象是,通过允许多个车辆提供单个节点的需求,我们基于RL的框架找到了比需要单一交付的解决方案更好的策略。我们获得了这种吸引人的特性,即所谓的分批交货,不需要任何手工工程,也没有额外的成本。
Attention
欢迎关注公众号《当交通遇上机器学习》!如果你和我一样是轨道交通、道路交通、城市规划相关领域的,可以加微信:Dr_JinleiZhang,备注“进群”,加入交通大数据交流群!希望我们共同进步!