机器学习（算法篇）——K-近邻算法

K-近邻算法简介

K-近邻算法(KNN)概念

K Nearest Neighbor算法又叫KNN算法，这个算法是机器学习里面一个比较经典的算法， 总体来说KNN算法是相对比较容易理解的算法。

定义:
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

距离公式：

两个样本的距离可以通过如下公式计算，又叫欧式距离 。

实现流程

(1）计算已知类别数据集中的点与当前点之间的距离

(2）按距离递增次序排序

(3）选取与当前点距离最小的k个点

(4）统计前k个点所在的类别出现的频率

(5）返回前k个点出现频率最高的类别作为当前点的预测分类

k近邻算法api初步使用

机器学习流程：

1.获取数据集
2.数据基本处理
3.特征工程
4.机器学习
5.模型评估

Scikit-learn工具介绍

Scikit-learn简介：

Python语言的机器学习工具
Scikit-learn包括许多知名的机器学习算法的实现
Scikit-learn文档完善，容易上手，丰富的API
目前稳定版本0.19.1

安装：

pip3 install scikit-learn==0.19.1

安装好之后可以通过以下命令查看是否安装成功

import sklearn

注：安装scikit-learn需要Numpy, Scipy等库

Scikit-learn包含的内容

分类、聚类、回归
特征工程
模型选择、调优

K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)

n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数

案例：

from sklearn.neighbors import KNeighborsClassifier

x=[[1],[2],[0],[0]]
y=[5,10,1,1]
estimator=KNeighborsClassifier(n_neighbors=2)
estimator.fit(x,y)
ret=estimator.predict([[1000]])

print(ret)

距离度量

欧式距离(Euclidean Distance)

欧氏距离是最容易直观理解的距离度量方法，我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。

曼哈顿距离(Manhattan Distance)

在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

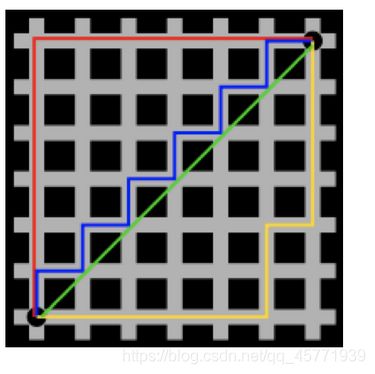
切比雪夫距离 (Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

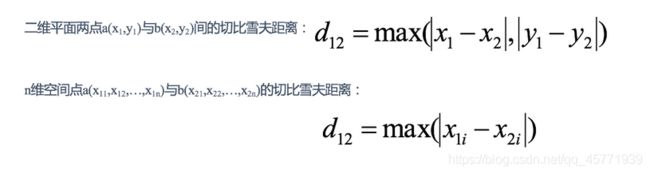
闵可夫斯基距离(Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

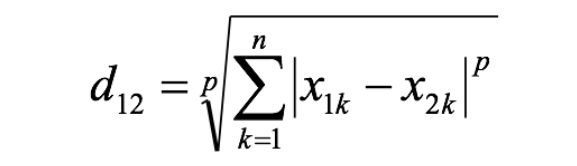
其中p是一个变参数：

当p=1时，就是曼哈顿距离；

当p=2时，就是欧氏距离；

当p→∞时，就是切比雪夫距离。

根据p的不同，闵氏距离可以表示某一类/种的距离。

标准化欧氏距离 (Standardized EuclideanDistance)

标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。

思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值(mean)为m，标准差(standard deviation)为s，X的“标准化变量”表示为：

如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)。

余弦距离(Cosine Distance)

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。
二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

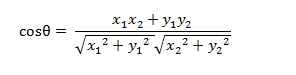
两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：

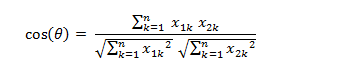
汉明距离(Hamming Distance)

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（相同长度）字对应位不同的数量，我们以d（x,y）表示两个字x,y之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

汉明距离的计算方式：计算两个等长字串之间对应位置上不同字符的个数。也就是说要求输入的两个字符串必须长度一致。

杰卡德距离(Jaccard Distance)

杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：

杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

马氏距离(Mahalanobis Distance)

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是，它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的），并且是尺度无关的(scale-invariant)，即独立于测量尺度。

对于一个均值为μ，协方差矩阵为Σ的多变量向量，其马氏距离为：

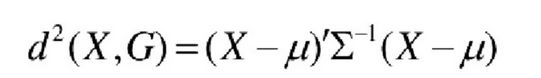
当m=1时

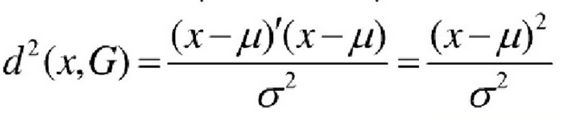
马氏距离特性：

1.量纲无关，排除变量之间的相关性的干扰；

2.马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

3 .计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

4.还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点（3，4），（5，6），（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

K值的选择

K值过小：

​

容易受到异常点的影响。

k值过大：

​

​ 受到样本均衡的问题

选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

K=N（N为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的K值。对这个简单的分类器进行泛化，用核方法把这个线性模型扩展到非线性的情况，具体方法是把低维数据集映射到高维特征空间。

近似误差：

对现有训练集的训练误差，关注训练集，如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。

估计误差：

可以理解为对测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型。

Kd树

实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。

k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很大时，计算非常耗时。

为了提高kNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

kd树：为了避免每次都重新计算一遍距离，算法会把距离信息保存在一棵树里，这样在计算之前从树里查询距离信息，尽量避免重新计算。其基本原理是，如果A和B距离很远，B和C距离很近，那么A和C的距离也很远。有了这个信息，就可以在合适的时候跳过距离远的点。这样优化后的算法复杂度可降低到O（DNlog（N））

数据集采集

案例：鸢尾花种类预测

Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。关于数据集的具体介绍：

scikit-learn数据集API介绍：

sklearn.datasets

加载获取流行数据集

datasets.load_*()

获取小规模数据集，数据包含在datasets里

datasets.fetch_*(data_home=None)

获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/

sklearn小数据集:

sklearn.datasets.load_iris()

加载并返回鸢尾花数据集

sklearn大数据集:

sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)

subset：‘train’或者’test’，‘all’，可选，选择要加载的数据集。
训练集的“训练”，测试集的“测试”，两者的“全部”

sklearn数据集返回值介绍:

load和fetch返回的数据类型datasets.base.Bunch(字典格式)

data：特征数据数组，是 [n_samples * n_features] 的二维 numpy.ndarray 数组
target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
DESCR：数据描述
feature_names：特征名,新闻数据，手写数字、回归数据集没有
target_names：标签名

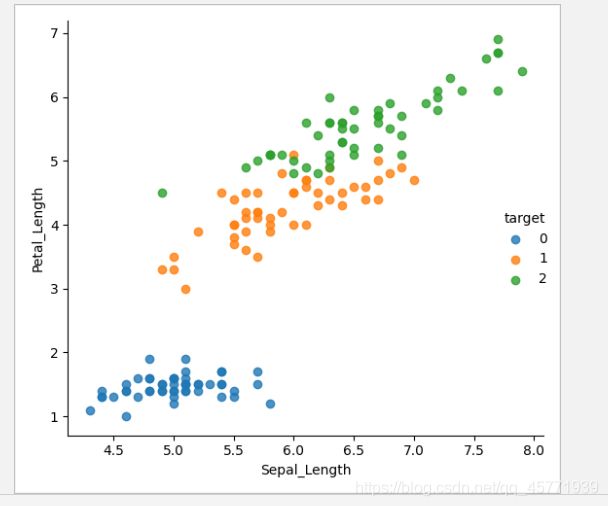
查看数据分布:
Seaborn 是基于 Matplotlib 核心库进行了更高级的 API 封装，可以让你轻松地画出更漂亮的图形。而 Seaborn 的漂亮主要体现在配色更加舒服、以及图形元素的样式更加细腻。

sns.lmplot() 里的 x, y 分别代表横纵坐标的列名,
data= 是关联到数据集,
hue=*代表按照 species即花的类别分类显示,
fit_reg=是否进行线性拟合。

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris=load_iris()
iris_d = pd.DataFrame(iris['data'], columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])

iris_d['target'] = iris.target

def plot_iris (iris,col1,col2):
    sns.lmplot(data=iris,x=col1,y=col2,hue = "target",fit_reg = False)
    plt.show()

plot_iris(iris_d,"Sepal_Length","Petal_Length")

数据集的划分:
机器学习一般的数据集会划分为两个部分：

训练数据：用于训练，构建模型
测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

训练集：70% 80% 75%
测试集：30% 20% 25%

数据集划分api

**sklearn.model_selection.train_test_split(arrays, *options)**
    x 数据集的特征值
    y 数据集的标签值
    test_size 测试集的大小，一般为float
    random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
    return 测试集特征训练集特征值值，训练标签，测试标签(默认随机取)

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()

x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=2)
print("x_train:\n", x_train.shape)
# 随机数种子
x_train1, x_test1, y_train1, y_test1 = train_test_split(iris.data, iris.target, random_state=6)
x_train2, x_test2, y_train2, y_test2 = train_test_split(iris.data, iris.target, random_state=6)
print("如果随机数种子不一致：\n", x_train == x_train1)
print("如果随机数种子一致：\n", x_train1 == x_train2)

特征工程-特征预处理

特征预处理定义

scikit-learn的解释

provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.

翻译过来：通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程。

为什么要进行归一化/标准化

特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征。

归一化

定义：

通过对原始数据进行变换把数据映射到(默认为[0,1])之间。

公式：

API：

sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )

MinMaxScalar.fit_transform(X)

X:numpy array格式的数据[n_samples,n_features]
返回值：转换后的形状相同的array。

注意：最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

标准化

定义：
通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内。

公式：

对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变
对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小

API:

sklearn.preprocessing.StandardScaler( )

处理之后每列来说所有数据都聚集在均值0附近标准差差为1

StandardScaler.fit_transform(X)

X:numpy array格式的数据[n_samples,n_features]
返回值：转换后的形状相同的array

案例：

import pandas as pd
from sklearn.preprocessing import StandardScaler

data = pd.read_csv("dating.txt")
print(data)
transfer = StandardScaler()
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("标准化的结果:\n", data)
print("每一列特征的平均值：\n", transfer.mean_)
print("每一列特征的方差：\n", transfer.var_)

流程实现

案例：鸢尾花种类预测

近邻算法API：

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)

n_neighbors：
int,可选（默认= 5），k_neighbors查询默认使用的邻居数

algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}

快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，

brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。

kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。

ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。

步骤分析

1.获取数据集
2.数据基本处理
3.特征工程
4.机器学习(模型训练)
5.模型评估

导入模块 ：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

1.获取数据集

iris = load_iris()

2.数据基本处理

x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2)

3.特征工程

transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

4.机器学习(模型训练)

estimator = KNeighborsClassifier(n_neighbors= 5)
estimator.fit(x_train,y_train)

5.模型评估

y_predict = estimator.predict(x_test)
print("预测结果为：\n",y_predict)
print("比对真实值和预测值:\n",y_predict == y_test)

score = estimator.score(x_test,y_test)
print("准确率为：\n",score)

全部代码：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1.获取数据集
iris = load_iris()

# 2.数据基本处理
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2)

# 3.特征工程：标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4.机器学习（模型训练）
estimator = KNeighborsClassifier(n_neighbors= 5)
estimator.fit(x_train,y_train)

# 5.模型评估
y_predict = estimator.predict(x_test)
print("预测结果为：\n",y_predict)
print("比对真实值和预测值:\n",y_predict == y_test)

score = estimator.score(x_test,y_test)
print("准确率为：\n",score)

交叉验证与网格搜索

交叉验证简介

交叉验证：将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成4份，其中一份作为验证集。然后经过4次(组)的测试，每次都更换不同的验证集。即得到4组模型的结果，取平均值作为最终结果。又称4折交叉验证。

我们之前知道数据分为训练集和测试集，但是为了让从训练得到模型结果更加准确。做以下处理

训练集：训练集+验证集
测试集：测试集

交叉验证目的：为了让被评估的模型更加准确可信。

网格搜索简介

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。交叉验证，网格搜索（模型选择与调优）API：
sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

对估计器的指定参数值进行详尽搜索
estimator：估计器对象
param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
cv：指定几折交叉验证
fit：输入训练数据
score：准确率

结果分析：
bestscore__:在交叉验证中验证的最好结果
bestestimator：最好的参数模型
cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

鸢尾花案例增加K值调优：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1.获取数据集
iris = load_iris()

# 2.数据基本处理
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2)

# 3.特征工程：标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4.机器学习（模型训练）
estimator = KNeighborsClassifier()
param_dict = {"n_neighbors":[1,3,5]}
estimator = GridSearchCV(estimator, param_grid = param_dict,cv=20,n_jobs=-1)
estimator.fit(x_train,y_train)

# 5.模型评估
y_predict = estimator.predict(x_test)
print("预测结果为：\n",y_predict)
print("比对真实值和预测值:\n",y_predict == y_test)

score = estimator.score(x_test,y_test)
print("准确率为：\n",score)


print("在交叉验证中验证的最好结果：\n", estimator.best_score_)
print("最好的参数模型：\n", estimator.best_estimator_)
print("每次交叉验证后的准确率结果：\n", estimator.cv_results_)