数据挖掘学习笔记之K-means算法

---

K-means(K-均值算法)算法背景

K-means聚类算法由J.B.MacQueen在1967年提出，是最为经典也是使用最为广泛的一种基于划分的聚类算法，属于基于距离的聚类算法。基于距离的聚类算法是指采用距离作为相似性度量的评价指标，也就是说当两个对象离的近，二者之间的距离比较小，那么它们之间的相似性就比较大。这类算法通常是由距离比较相近的对象组成簇，把得到紧凑而且独立的簇作为最终目标，因此将这类算法称为基于距离的聚类算法。K-means聚类算法是其中比较经典的一种算法。K-means聚类是数据挖掘的重要分支，也是实际应用中最常用的聚类算法之一。

什么是k-means算法?

K-means算法是一种无监督的聚类算法

K-means算法的核心目标?

核心目标:将给定的数据划分成k个簇,并且给出每个簇的中心点,即质心

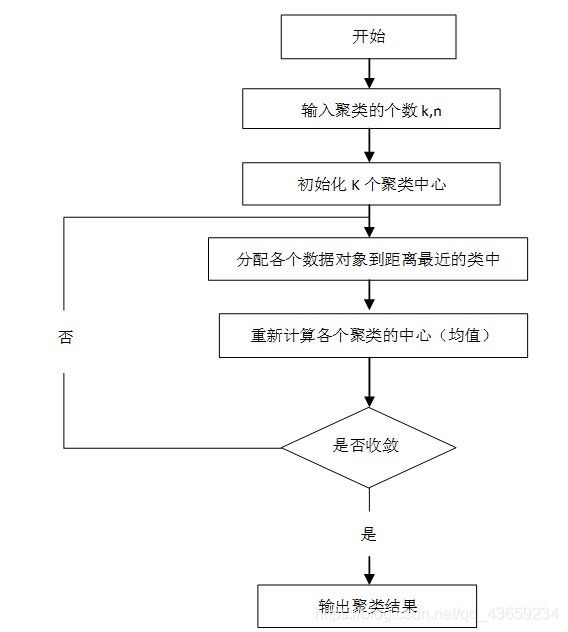
K-means算法工作流程

K-means实例

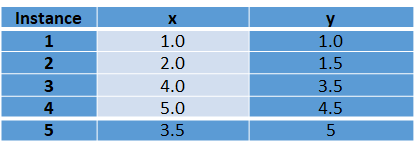
（1）设置 K 值为2。
（2）任意选择两个点分别作为两个簇的初始簇中心。假设选择instance 1(1.0,1.0)作为第1个簇中心， instance 2(2.0,1.5)作为第2个簇中心。
（3）使用Distance(A-B)=sqrt((x1-x2)^2 + (y1-y2)^2)两点之间的距离公式，计算其余实例与两个簇中心的简单欧氏距离（Euclidean Distance），结果如下表所示。

（4）重新计算新的簇中心。
对于簇1簇中心不变，即C1 = (1.0,1.0)。
对于簇2：x = (2.0+4.0+5.0+3.5) / 4 = 3.625，y = (1.5+3.5+4.5+5) / 4 = 3.625。
得到新的簇中心C1= (1.0,1.0) 和 C2= (3.625,3.625)，因为簇中心发生了变化，算法必须执行第二次迭代，重复步骤（3）。
第二次迭代之后的结果导致了簇的变化：{1,2}和{3,4,5}。
（5）重新计算每个簇中心。
对于簇1：x = (1.0+2.0) / 2= 1.5，y = (1.0+1.5) / 2 = 1.25。
对于簇2：x = (2.0+5.0+3.5) / 3= 4.17，y = (3.5+4.5+5) / 3 = 4.33。
这次迭代后簇中心再次改变。因此，该过程继续进行第三次迭代，结果形成{1,2}和{3,4,5}两个簇，与第二次迭代后形成的簇完全一样，若继续计算新簇中心的话，簇中心的值一定不变，至此，算法结束。

K-means总结

优点:
(1)k-均值算法原理简单，容易实现，且运行效率比较高
(2)k-均值算法聚类结果容易解释，适用于高维数据的聚类
(3)对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目，t是迭代的次数。通常地k< (4)算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，而簇与簇之间区别明显时，它的聚类效果较好。
缺点:
(1)k-均值算法采用贪心策略，导致容易局部收敛，在大规模数据集上求解较慢
(2)k-均值算法对离群点和噪声点非常敏感，少量的离群点和噪声点可能对算法求平均值产生极大影响，从而影响聚类结果
(3)k-均值算法中初始聚类中心的选取也对算法结果影响很大，不同的初始中心可能会导致不同的聚类结果。对此，研究人员提出k-均值++算法，其思想是使初始的聚类中心之间的相互距离尽可能远

K-means算法python实现

import pandas as pd
import random
import time
import json
import numpy as np
import matplotlib.pyplot as plt
class K_means(object):
    def __init__(self):
        self.df = pd.read_csv('xclara.csv')
        print(self.df)
        self.num = int(input('请输入聚类中心的个数'))
        self.core = []
        self.x1_list = []
        self.x2_list = []
        self.x3_list = []
        self.y1_list = []
        self.y2_list = []
        self.y3_list = []
        self.distance1 = []
        self.List = [[],[],[]]

        for i in range(0,self.num):

            self.core.append(self.df.loc[random.randint(0,3000),:])
        self.plot()

    def First(self):
        for j2 in range(0,3000):

            for i1 in range(0,len(self.core)):
                self.X = ((self.core[i1]['V1']) - (self.df.loc[j2,'V1']))**2

                self.Y = ((self.core[i1]['V2']) - (self.df.loc[j2,'V2']))**2
                self.distance = (self.X+self.Y)**(1/2)
                self.distance1.append(self.distance)

            self.min_distance = min(self.distance1)

            self.List[self.distance1.index(self.min_distance)].append(self.df.loc[j2,:])
            self.distance1 = []
    def circulate(self):
        self.First()
        for i in range(0,3):
            self.sum = 0
            self.sum1 = 0
            for j in range(0,len(self.List[i])):
                self.sum = self.sum + self.List[i][j]['V1']
                self.sum1 = self.sum1 + self.List[i][j]['V2']
            self.x_mean = self.sum/len(self.List[i])
            self.y_mean = self.sum1/len(self.List[i])
            self.core[i] = pd.Series(data={'V1':self.x_mean,'V2':self.y_mean})
            print(self.core[i])
            print(type(self.core[i]))
            self.List2 = self.List
        self.List = [[],[],[]]
    def A(self):
        for i4 in range(15):
            self.circulate()
    def plot(self):
        self.A()
        plt.rcParams['font.sans-serif']=['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        plt.xlabel('X')
        plt.ylabel('Y')
        plt.xlim(xmax=-100,xmin=100)
        plt.ylim(ymax=-100,ymin=100)
        for i in range (0,len(self.List2)):
            for j in range(0,len(self.List2[i])):
                self.x1 = self.List2[i][j]['V1']
                self.y1 = self.List2[i][j]['V2']
                if i ==0:
                    self.x1_list.append(self.x1)
                    self.y1_list .append(self.y1)
                if i ==1:
                    self.x2_list.append(self.x1)
                    self.y2_list .append(self.y1)
                if i ==2:
                    self.x3_list.append(self.x1)
                    self.y3_list .append(self.y1)
                self.colors1 = '#00CED1' #点的颜色
                self.colors2 = '#DC143C'
                self.colors3 = '#7FFFD4'
                self.area = np.pi * 2  # 点面积
        self.np_x1 = np.array(self.x1_list)
        self.np_x2 = np.array(self.x2_list)
        self.np_x3 = np.array(self.x3_list)
        self.np_y1 = np.array(self.y1_list)
        self.np_y2 = np.array(self.y2_list)
        self.np_y3 = np.array(self.y3_list)
        plt.scatter(self.np_x1, self.np_y1, s=self.area, c=self.colors1, alpha=0.4, label='类别A',marker='1')
        plt.scatter(self.np_x2, self.np_y2, s=self.area, c=self.colors2, alpha=0.4, label='类别B',marker='p')
        plt.scatter(self.np_x3, self.np_y3, s=self.area, c=self.colors3, alpha=0.4, label='类别C',marker='*')
        plt.legend()
        plt.savefig('julei2.png', dpi=300)
        plt.show()
# 画散点图
K_means = K_means()