Detection:目标检测常用评价指标的学习总结(IoU、TP、FP、TN、FN、Precision、Recall、F1-score、P-R曲线、AP、mAP、 ROC曲线、TPR、FPR和AUC)
目录
- 前言
- 1. IoU
- 2. TP、FP、TN、FN
-
- 2.1 混淆矩阵
- 2.2 TP、FP、TN、FN的定义
- 2.3 TP、FP、TN、FN在目标检测中的对应内容
-
- 2.3.1 TP,FP在目标检测中的理解
- 2.3.2 TN,FN在目标检测中的理解
- 2.3.3 总结
- 3. Accuracy、Precision、Recall和 F 1 F_{1} F1-score指标
-
- 3.1 Accuracy
- 3.2 单类别下的Precision、recall和 F 1 F_{1} F1-score的计算方法
-
- 3.2.1 Precision
- 3.2.2 Recall
- 3.2.3 Precision和Recall的侧重
- 3.2.4 F 1 F_{1} F1-score
- 3.3 多类别下的Precision、Recall和 F 1 F_{1} F1-score的计算方法
-
- 3.3.1 宏平均(Macro-average)方法
- 3.3.2 加权平均(Weighted-average)方法
- 3.3.3 微平均(Micro-average)方法
- 3.3.4 讨论
- 4. P-R曲线、AP和mAP
-
- 4.1 P-R曲线
- 4.2 AP和mAP
- 4.3 yolo中[email protected]与[email protected]:0.95的含义
- 5. ROC曲线和AUC
-
- 5.1 TPR、FPR、FNR和TNR
- 5.2 ROC曲线的定义
- 5.3 AUC
- 5.4 P-R曲线和ROC曲线的区别
- 总结
- 附录1 基于yolov5的计算指标代码,举例计算P-R曲线和ap值,mAP值。
前言
刚开始学习目标检测的时候常常弄不清楚TP,FP,TN,FN对应的目标框是什么、P-R曲线是什么、AUC又是什么等等问题。因此,本人借此机会对这些内容进行了深入学习,并进行整理总结。现在分享给各位读者朋友。
由于本文目前是我写的最多的一篇文章,难免存在一些错误。如果读者朋友发现了,麻烦在评论区告知我,我及时改正。 ⌣ ¨ \ddot\smile ⌣¨
对于前置内容有一定了解且只想查看指定指标的,可以从目录直接跳转。如果前置内容不熟悉的读者,建议从头开始看。
本篇文章主要分为5个部分:
- 第一部分介绍IoU这个指标的含义和计算方法。
- 第二部分介绍TP、FP、TN、FN这四个指标的含义,以及在目标检测中的使用方法。
- 第三部分介绍Accuracy、Precision、Recall、F1-score这四个指标的含义,以及在单类别和多类别下的计算方法。
- 第四部分介绍P-R曲线、AP和mAP这个三个指标的含义和计算方法。
- 第五部分介绍ROC曲线和AUC这个两指标的含义和计算方法。
- 最后还附上了yolov5计算指标代码的部分解释,并举例说明。详情参见附录。
本篇博客的参考资料如下:
- 作者:TODAY’S,目标检测指标TP、FP、TN、FN和Precision、Recall。
- 作者:虎大猫猫一,文讲清楚目标检测中mAP、AP、precison、recall、accuracy、TP、FP、FN、TN
- 作者:小小詹同学, FP、FN、TP、TN、精确率(Precision)、召回率(Recall)、准确率(Accuracy)评价指标详述
- 作者:NaNNN,多分类模型Accuracy, Precision, Recall和F1-score的超级无敌深入探讨
- 作者:daige123, 学习笔记3——目标检测的评价指标(AC、TP、FP、FN、TN、AP、ROC、AUC、mAP、[email protected]、[email protected]:.95
- 作者:Matrix_11, 机器学习 F1-Score, recall, precision
- 作者: 山竹小果, 评价指标整理:Precision, Recall, F-score, TPR, FPR, TNR, FNR, AUC, Accuracy
- 作者:流星落, [email protected]与[email protected]:0.95的含义,YOLO
- 作者:吴良超的学习笔记,ROC 曲线与 PR 曲线
- 作者:希葛格的韩少君, 目标检测中的AP,mAP
- 维基百科:ROC曲线
- An introduction to ROC analysis
- 作者:满船清梦压星河HK【python numpy】a.cumsum()、np.interp()、np.maximum.accumulate()、np.trapz()
1. IoU
定义:IoU(Intersection Over Union)交占比,该指标常用来表示预测框和真实框的相近程度。其计算方法为两个框交集的面积除以两个框并集的面积。公式如下:
I o U = A ∩ B A ∪ B , A , B 分别表示预测框和真实框。 IoU = \frac{A\cap B}{A\cup B}, A,B分别表示预测框和真实框。 IoU=A∪BA∩B,A,B分别表示预测框和真实框。
图片表示如下,蓝色部分为A和B计算得到的面积。
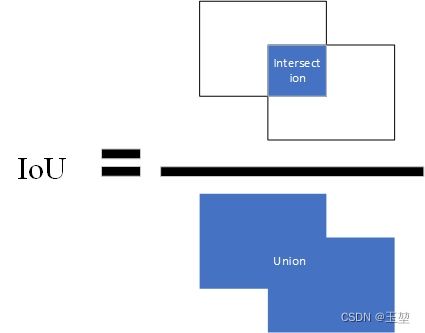
IoU还有其他的变种,如CIoU,DIoU,GIoU等,本文不做过多介绍。我会单独列出一篇文章总结。如果读者朋友现在感兴趣可以参考其他博客的介绍。
2. TP、FP、TN、FN
2.1 混淆矩阵
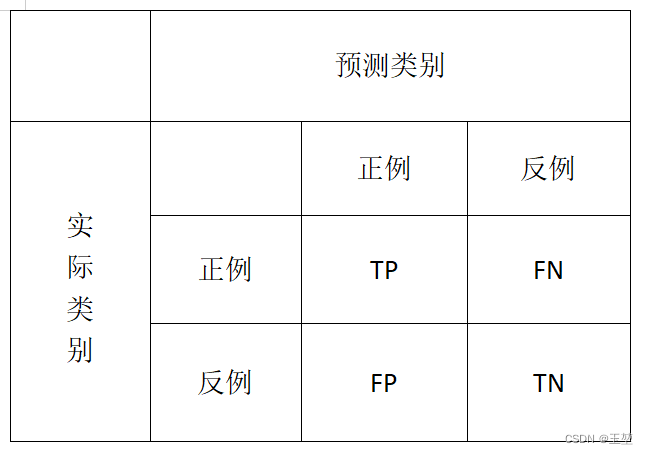
提到TP、FP、TN、FN,首先我们得了解一下混淆矩阵。
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。
混淆矩阵的每一列代表了预测类别,每一列的总数表示预测为该类别的数据的数目;每一行代表了数据的真实归属类别,每一行的数据总数表示该类别的数据实例的数目。
举例说明如下:(图片来自百度百科)
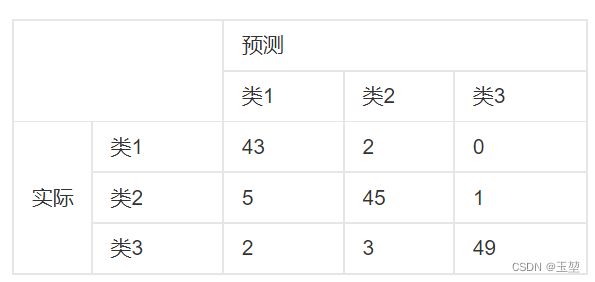
其中,第一行第一列的43表示原本属于类1,且预测为类1的数量为43。
第二行第一列的5表示原本属于类2,且预测为类1的数量为5。
其余数目同理。
第一列总数43+5+2=50,表示全部预测为类1的数目为50。
第一行总数43+2=45,表示全部原本属于类1的数目是45。
其余数目同理。
2.2 TP、FP、TN、FN的定义
经过混淆矩阵的理解,此处就可以引出TP、FP、TN、FN的定义:
TP(True Positive): 真正例,表示预测为正例(positive),且预测正确(true),即原本为正例。
FN(False Negative): 假反例,表示预测结果为反例(negative),且预测错误(false),即原本为正例。
FP(False Positive): 假正例,表示预测结果为正例(positive),且预测错误(false),即原本为反例。
TN(true Negative): 真反例,表示预测结果为反例(negative),且预测正确(true),即原本为反例。
个人记忆的方法是,后面的字母表示预测的结果,前面的字母表示预测的正确与否。
2.3 TP、FP、TN、FN在目标检测中的对应内容
在目标检测中,我们经过网络会获取许多的预测框和其对应的置信度打分(confidence score)。首先,通过对比预先设定的置信度阈值(confidence threshold)来过滤预测框。其中高于置信度阈值的预测框将其看作正例(positive),低于置信度阈值的预测框在目标检测中一般舍弃不用。
2.3.1 TP,FP在目标检测中的理解
这两个指标可以成对讲,在所有保留的预测框中(即所有的positive中),通过IoU阈值来判断预测结果。大于IoU阈值的为预测正确(true),小于IoU阈值的为预测错误(false)。但是要注意一点,对于每个目标而言,TP只有一个,因此在大于IoU阈值的预测框中,选取IoU值最大的一个预测框为TP,其他所有的预测框都为FP。小于IoU阈值预测框也是FP。
以二分类为例,举例如下:
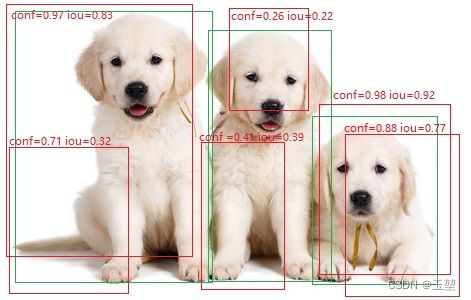
如图所示,绿框是真实框,记为GT(ground true)。红色为预测框。在下述图中有三只可爱的狗,即三个目标,GT=3。且假设,置信度阈值和IoU阈值都为0.5。
此时,从下图可以看出,大于置信度阈值的预测框有4个,即这4个框都为正例(positive),小于置信度阈值的框有两个(conf=0.26和conf=0.41的两个框),则这两个框为负例(negative)。在预测为正例的预测框中,小于IoU阈值的预测框只有一个,即IoU=0.32的预测框,那么该预测框为FP。再看剩下的3个预测框,基于上面的原则,对于左边的目标而言,IoU=0.83的预测框满足TP的定义。对于右边的预测框而言,虽然,IoU=0.92和IoU=0.77的预测框都预测正确,且大于IoU阈值,但是我们只选择其中IoU最高的作为TP。余下IoU=0.77的预测框则作为FP。 最后,我们就会得到FP=2(IoU=0.32的框和IoU=0.77的框),TP=2(IoU=0.83的框和IoU=0.92的框)。
(图片来自百度百科,里面的框,conf和iou值都是p上去的,且数据是编的。仅供理解TP和FP的概念使用)
2.3.2 TN,FN在目标检测中的理解
这两个指标也可以一起讲。在目标检测中,负例本身就不存在。因此,对于FN而言,我们取没有预测出来的目标数量作为FN。对于TN而言,目标检测不使用这个概念。
注意:无论小于置信度的预测框有多少个,我们都不做考虑。只取没有预测出来的目标的数量作为FN。
以二分类为例,举例如下:
如图所示,绿框是真实框,记为GT(ground true)。红色为预测框。在下述图中有三只可爱的狗,即三个目标,GT=3。且假设,置信度阈值和IoU阈值都为0.5。
根据2.3.1节中的例子,下图中左右两个目标被预测出来,中间的小狗没有预测出来。因此,FN=1。
此时,我们并不关心小于置信度阈值的两个框(conf=0.26的预测框和conf=0.41的预测框)。
2.3.3 总结
(1)大于置信度阈值的预测框全部都表示预测为正例(positive)
(2)TP:IoU>IoU阈值的预测框数量,同一个目标只取最大IoU值的预测框,即一个目标只有一个TP。
(3)FP:IoU
(5)FN:没有检测到的目标的数量。
(6)FN和TP之和表示所有的目标数量,即FN+TP=GT。
3. Accuracy、Precision、Recall和 F 1 F_{1} F1-score指标
3.1 Accuracy
Accuracy,中文又称准确率。该指标表示在模型预测的所有测试框(TP+FP+TN+FN)中,预测正确的测试框(TP+TN)的占比。公式如下:
A c c = T P + T N T P + F P + T N + F N Acc = \frac{TP+TN}{TP+FP+TN+FN} Acc=TP+FP+TN+FNTP+TN
准确率表示模型预测目标的能力。区别于后续的Precision和Recall只针对正例,准确率针对的是所有样本,既包含正例也包含反例。
准确率常用于分类模型,在目标检测中很少提及。这是因为Accuracy无法解决类别不平衡的问题。假设,有100张图片,其中90张是狗,6张是猫,4张是鸟。如果模型无论输入什么图片都预测为狗的话,此时Accuracy就可以达到90%,这种情况下,模型显然是没有任何学习能力的,但是Accuracy却很高。在目标检测中,由于场景的复杂性,经常会出现目标类别不平衡的情况。此时使用Accuracy效果并不理想,因此才引入了精确率(Precision)和召回率(Recall)。
Accuracy针对的是全部样本,而Precision和Recall针对的是每个类别。这样Precision和Recall就可以方便的处理多类别下类别不平衡的情况,以下章节分别介绍了单类别目标检测的Precision,Recall、 F 1 F_{1} F1-score的计算方法,和多类别下Precision,Recall、 F 1 F_{1} F1-score的计算方法。
3.2 单类别下的Precision、recall和 F 1 F_{1} F1-score的计算方法
3.2.1 Precision
Precision,中文又称精确率,或查准率。该指标表示在所有预测为正例的测试框(TP+FP)中,预测为正例且正确的测试框(TP)的占比。公式如下:
P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP
查准率表示模型预测正确物体的能力。当查准率为0时,模型预测出来的所有正例都是错误的。当查准率为1时,模型预测出来的所有正例都是正确的。查准率越高表示模型预测出来的所有正例中大部分都是正确的目标,只有少量不是目标的物体被识别为目标。
3.2.2 Recall
Recall,中文又称召回率,或查全率(有时也被成为灵敏度)。该指标表示在所有的正例(TP+FN)中,模型预测为正例且正确的目标(TP)的占比。公式如下:
R = T P T P + F N = T P G T R =\frac{TP}{TP+FN} = \frac{TP}{GT} R=TP+FNTP=GTTP
查全率表示模型能够找全正确物体的能力。当查全率为0时,模型一个正确的正例都没有找到,当查全率为1时,所有的正确的正例都被找到。查全率越高,表示模型能够找到更多的正确的正例。
总结:
Precision着重评估:在预测为Positive的所有数据中,真实Positve的数据到底占多少?
Recall着重评估:在所有的Positive数据中,到底有多少数据被成功预测为Positive?
3.2.3 Precision和Recall的侧重
Recall和Precision之间是个矛盾的指标,当Precision高的时候,往往Recall就低。同理,当Recall高的时候,往往Precision就低。那么对于Recall和Precision之间的侧重就取决于当前应用的环境。举例如下:
(1)注重Recall指标的情况。
当面前站了10个人,里面有8个平民(negative),2个罪犯(positive)。此时我们就更加注重recall,我们宁愿把平民错认为罪犯(FP),也要把减少把罪犯认成平民(FN),避免让罪犯成为漏网之鱼。因此,我们更加注重预测的查全率,减少漏检,有一种宁杀错不放过的感觉。回顾Recall的公式,可以得出,这种情况我们更注重Recall,而不是Precision。
(2)注重Precision指标的情况。
目前有10份邮件,其中8个正常邮件(negative),2个垃圾邮件(positive)。此时我们更加注重Precision,我们宁愿把垃圾邮件检测为正常邮件(FN),也不能把正常邮件检测为垃圾邮件(TP),避免错过重要信息。因此,我们更加预测的准确性,减少误检。回顾Precision的公式,可以得出,这种情况我们更注重Precision,而不是Recall。
3.2.4 F 1 F_{1} F1-score
F 1 F_{1} F1-score其实是 F β F_{\beta} Fβ-score的一个特例( β = 1 \beta=1 β=1), 是Precision指标和Recall指标的调和平均值。用来平衡Precision指标和Recall指标,使得模型更加稳定,不会偏向于Precision指标和Recall指标的任意一个。
在介绍F1-score 之前,我们先学习下更通用的形式 F β F_{\beta} Fβ-score,这个指标是也是用来衡量Precision指标和Recall指标的,不过可以通过 β \beta β来设置模型对于Precision指标和Recall指标的偏好。
F β F_{\beta} Fβ-score个公式如下:
F β − s c o r e = ( 1 + β 2 ) ∗ P r e c i s i o n ∗ R e c a l l β 2 ∗ P r e c i s i o n + R e c a l l F_{\beta}-score = \frac{(1+\beta^2)*Precision*Recall}{\beta^2*Precision + Recall} Fβ−score=β2∗Precision+Recall(1+β2)∗Precision∗Recall
从上述的公式中可以看出,如果 β \beta β>1分母中Precision的权重很大,为了使 F β − s c o r e F_{\beta}-score Fβ−score指标更高,我们希望Precision很小,此时相对的Recall就越大(从P-R曲线上看,Precision和Recall是相矛盾的数据。P-R曲线后续章节会介绍)。则 β \beta β>1的情况下,说明模型更偏好于提升Recall,此时模型更偏向于查全的能力。相反, β \beta β<1分母中Recall的权重很大,为了使 F β − s c o r e F_{\beta}-score Fβ−score指标更高,我们希望Recall很小,此时相对的Precision就越大。则 β \beta β<1的情况下,说明模型更偏好于提升Precision,此时模型更偏向于查准的能力。为使模型即不具有偏向性,又可以同时评估Precision指标和Recall指标,我们选用 β \beta β=1,即F1-score来作为模型的调和平均值,从而描述模型的稳定性
F 1 F_{1} F1-score个公式如下:
F 1 − s c o r e = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F_{1}-score = \frac{2*Precision*Recall}{Precision + Recall} F1−score=Precision+Recall2∗Precision∗Recall
F1-score既不是算数平均 P + R 2 \frac{P+R}{2} 2P+R,也不是几何平均 P R \sqrt{PR} PR,而是调和平均数 1 F 1 = 1 2 ( 1 P + 1 R ) \frac{1}{F_1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R}) F11=21(P1+R1),即 F 1 = 2 P R P + R F_{1} = \frac{2PR}{P + R} F1=P+R2PR。
3.3 多类别下的Precision、Recall和 F 1 F_{1} F1-score的计算方法
以上都是单类别下的Precision和Recall的计算方法。当遇到多类别的情况时,我们就有以下3种方法,分别是 宏平均(Macro-average)方法,加权平均(Weighted-average)方法和微平均(Micro-average)方法。分别介绍如下:
3.3.1 宏平均(Macro-average)方法
宏平均方法,通过计算每个类别的Precision和Recall,然后加起来求平均。这种方法是将所有的类别都默认一样的权重,但是它的值会受稀有类别影响。
举例说明:
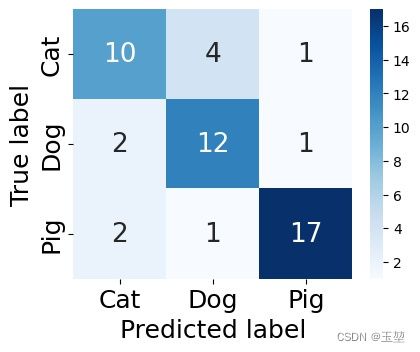
假设有三个类别,分别是猫,狗,鸟,一共50个样本, 其中猫15只,狗15只,鸟20只。模型预测结果如下图所示,现在要计算全部类别的Precision和Recall。
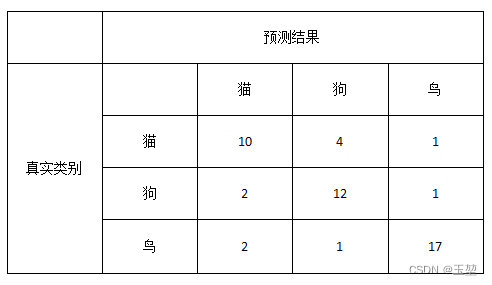
代码生成混淆矩阵:
import numpy as np
import seaborn as sns
from sklearn.metrics import confusion_matrix
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, average_precision_score, precision_score, f1_score,recall_score
# 创建数据
y_true = np.array(["cat"]*15 + ["dog"]*15 + ["bird"]*20)
y_pred = np.array(["cat"]*10 + ["dog"]*4 + ["bird"]*1 +
["cat"]*2 + ["dog"]*12 + ["bird"]*1 +
["cat"]*2 + ["dog"]*1 + ["bird"]*17)
# 生成混淆矩阵
cm = confusion_matrix(y_true, y_pred, labels=["cat", "dog", "bird"])
# # 创建数据,用数字也是可以。
# y_true = np.array([0]*15 + [1]*15 + [2]*20)
# y_pred = np.array([0]*10 + [1]*4 + [2]*1 +
# [0]*2 + [1]*12 + [2]*1 +
# [0]*2 + [1]*1 + [2]*17)
# # 生成混淆矩阵
# cm = confusion_matrix(y_true, y_pred)
# 给混淆矩阵添加索引。
conf_matrix = pd.DataFrame(cm, index=['Cat','Dog','Pig'], columns=['Cat','Dog','Pig'])
# 显示混淆矩阵。
fig, ax = plt.subplots(figsize = (4.5,3.5))
sns.heatmap(conf_matrix, annot=True, annot_kws={"size": 19}, cmap="Blues")
plt.ylabel('True label', fontsize=18)
plt.xlabel('Predicted label', fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.savefig('confusion.jpg', bbox_inches='tight')
plt.show()
我们采用宏平均算法。首先,先对每个类别分别计算Precision和Recall。对于猫而言,其TP,FP,FN如下图所示:
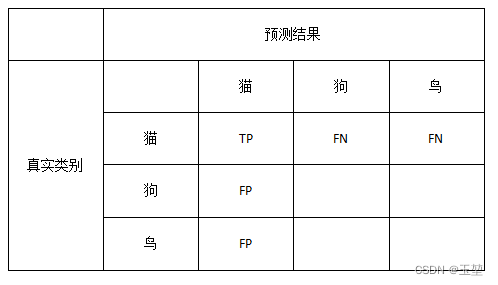
根据图中的显示,猫的Precision和Recall分别为:(P和R是Precision和Recall的简写)
P c a t = T P T P + F P = 10 10 + 2 + 2 ≈ 0.714 P_{cat} = \frac{TP}{TP+FP}=\frac{10}{10+2+2} \approx 0.714 Pcat=TP+FPTP=10+2+210≈0.714
R c a t = T P T P + F N = 10 10 + 4 + 1 ≈ 0.667 R_{cat} = \frac{TP}{TP+FN}=\frac{10}{10+4+1} \approx 0.667 Rcat=TP+FNTP=10+4+110≈0.667
F 1 c a t = 2 ∗ P c a t ∗ R c a t P c a t + R c a t = 2 ∗ 0.714 ∗ 0.667 0.714 + 0.667 ≈ 0.69 {F_{1}}_{cat} = \frac{2*P_{cat}*R_{cat}}{P_{cat} + R_{cat}} = \frac{2 * 0.714 * 0.667}{0.714 + 0.667} \approx 0.69 F1cat=Pcat+Rcat2∗Pcat∗Rcat=0.714+0.6672∗0.714∗0.667≈0.69
同理,狗的Precision和Recall为:
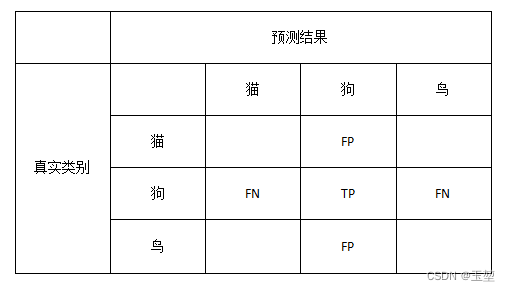
P d o g = T P T P + F P = 12 12 + 4 + 1 ≈ 0.706 P_{dog} = \frac{TP}{TP+FP}=\frac{12}{12+4+1} \approx 0.706 Pdog=TP+FPTP=12+4+112≈0.706
R d o g = T P T P + F N = 12 12 + 2 + 1 = 0.8 R_{dog} = \frac{TP}{TP+FN}=\frac{12}{12+2+1} = 0.8 Rdog=TP+FNTP=12+2+112=0.8
F 1 d o g = 2 ∗ P d o g ∗ R d o g P d o g + R d o g = 2 ∗ 0.706 ∗ 0.8 0.706 + 0.8 ≈ 0.75 {F_{1}}_{dog} = \frac{2*P_{dog}*R_{dog}}{P_{dog} + R_{dog}} = \frac{2 * 0.706 * 0.8}{0.706 + 0.8} \approx 0.75 F1dog=Pdog+Rdog2∗Pdog∗Rdog=0.706+0.82∗0.706∗0.8≈0.75
鸟的Precision和Recall为:
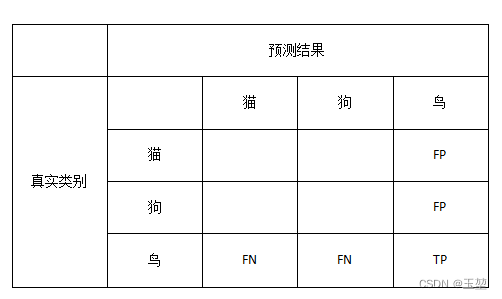
P b i r d = T P T P + F P = 17 17 + 1 + 1 ≈ 0.895 P_{bird} = \frac{TP}{TP+FP}=\frac{17}{17+1+1} \approx 0.895 Pbird=TP+FPTP=17+1+117≈0.895
R b i r d = T P T P + F N = 17 17 + 2 + 1 = 0.85 R_{bird} = \frac{TP}{TP+FN}=\frac{17}{17+2+1} = 0.85 Rbird=TP+FNTP=17+2+117=0.85
F 1 b i r d = 2 ∗ P b i r d ∗ R b i r d P b i r d + R b i r d = 2 ∗ 0.895 ∗ 0.85 0.895 + 0.85 ≈ 0.872 {F_{1}}_{bird} = \frac{2*P_{bird}*R_{bird}}{P_{bird} + R_{bird}} = \frac{2 * 0.895 * 0.85}{0.895 + 0.85} \approx 0.872 F1bird=Pbird+Rbird2∗Pbird∗Rbird=0.895+0.852∗0.895∗0.85≈0.872
此时,基于宏平局方法下的多类别Precision、Recall和F1-score的计算方法为:
P M a c r o − a v e r a g e = P c a t + P d o g + P b i r d 3 = 0.714 + 0.706 + 0.895 3 ≈ 0.772 P_{Macro-average} = \frac{P_{cat}+P_{dog}+P_{bird}}{3}=\frac{0.714+0.706+0.895}{3} \approx 0.772 PMacro−average=3Pcat+Pdog+Pbird=30.714+0.706+0.895≈0.772
R M a c r o − a v e r a g e = R c a t + R d o g + R b i r d 3 = 0.667 + 0.8 + 0.85 3 ≈ 0.772 R_{Macro-average} = \frac{R_{cat}+R_{dog}+R_{bird}}{3}=\frac{0.667+0.8+0.85}{3} \approx0.772 RMacro−average=3Rcat+Rdog+Rbird=30.667+0.8+0.85≈0.772
F 1 M a c r o − a v e r a g e = F 1 c a t + F 1 d o g + F 1 b i r d 3 = 0.69 + 0.75 + 0.872 3 ≈ 0.771 F1_{Macro-average} = \frac{{F_{1}}_{cat} + {F_{1}}_{dog} + {F_{1}}_{bird}}{3} = \frac{0.69 + 0.75 + 0.872}{3} \approx 0.771 F1Macro−average=3F1cat+F1dog+F1bird=30.69+0.75+0.872≈0.771
使用scikit-learn包进行代码验证:
# 计算指标
# 宏平均方法
P_Macro_average = precision_score(y_true, y_pred, average="macro")
R_Macro_average = recall_score(y_true, y_pred, average="macro")
F1_Macro_average = f1_score(y_true, y_pred, average="macro")
print("Base Macro_average method, the precision is {}, recall is {}, and f1_score is {}".format(P_Macro_average, R_Macro_average, F1_Macro_average))
结果展示如下(由于个人计算时,多次近似的原因,可能在小数位上略有不同):

3.3.2 加权平均(Weighted-average)方法
加权平均方法,首先计算单类别样本的Precision和Recall。然后计算每个类别的数据量占比,并记作类别权重。最后,计算类别权重与对应类别Precision和Recall的加权和,该结果即为多类别下的Precision和Recall。
与宏平均方法相比,加权平均是根据对应类别的占比来计算权重的,因此,它的值会受主要类别(数量占比大的类别)影响。
举例说明:
假设有三个类别,分别是猫,狗,鸟,一共50个样本, 其中猫15只,狗15只,鸟20只。模型预测结果如下图所示,现在要计算全部类别的Precision和Recall。

通过宏平均方法中,我们获取到了每个类别的对应的Precision和Recall。结果如下:
P c a t ≈ 0.714 R c a t ≈ 0.667 F 1 c a t ≈ 0.69 P_{cat} \approx 0.714 \quad R_{cat} \approx 0.667 \quad {F_{1}}_{cat} \approx 0.69 Pcat≈0.714Rcat≈0.667F1cat≈0.69
P d o g ≈ 0.706 R d o g = 0.8 F 1 d o g ≈ 0.75 P_{dog} \approx 0.706 \quad R_{dog} = 0.8 \quad {F_{1}}_{dog} \approx 0.75 Pdog≈0.706Rdog=0.8F1dog≈0.75
P b i r d ≈ 0.895 R b i r d = 0.85 F 1 b i r d ≈ 0.872 P_{bird} \approx 0.895 \quad R_{bird} = 0.85\quad{F_{1}}_{bird}\approx 0.872 Pbird≈0.895Rbird=0.85F1bird≈0.872
接下来,计算每个类别对应的数据占比:
W c a t = 15 50 = 0.3 W_{cat} = \frac{15}{50} = 0.3 Wcat=5015=0.3
W d o g = 15 50 = 0.3 W_{dog} = \frac{15}{50} = 0.3 Wdog=5015=0.3
W b i r d = 20 50 = 0.4 W_{bird} = \frac{20}{50} = 0.4 Wbird=5020=0.4
最后,计算类别权重和对应Precision和Recall的加权和:
P W e i g h t e d − a v e r a g e = W c a t ∗ P c a t + W d o g ∗ P d o g + W b i r d ∗ P b i r d P_{Weighted-average} = W_{cat} * P_{cat} + W_{dog} * P_{dog} + W_{bird} * P_{bird} PWeighted−average=Wcat∗Pcat+Wdog∗Pdog+Wbird∗Pbird
= 0.3 ∗ 0.714 + 0.3 ∗ 0.706 + 0.4 ∗ 0.895 = 0.784 = 0.3 * 0.714 + 0.3 * 0.706 + 0.4 * 0.895 = 0.784 =0.3∗0.714+0.3∗0.706+0.4∗0.895=0.784
R W e i g h t e d − a v e r a g e = W c a t ∗ R c a t + W d o g ∗ R d o g + W b i r d ∗ R b i r d R_{Weighted-average} = W_{cat} * R_{cat} + W_{dog} * R_{dog} + W_{bird} * R_{bird} RWeighted−average=Wcat∗Rcat+Wdog∗Rdog+Wbird∗Rbird
= 0.3 ∗ 0.667 + 0.3 ∗ 0.8 + 0.4 ∗ 0.85 = 0.7801 = 0.3 * 0.667+ 0.3 * 0.8+ 0.4 * 0.85 = 0.7801 =0.3∗0.667+0.3∗0.8+0.4∗0.85=0.7801
F 1 W e i g h t e d − a v e r a g e = W c a t ∗ F 1 c a t + W d o g ∗ F 1 d o g + W b i r d ∗ F 1 b i r d {F_{1}}_{Weighted-average} = W_{cat} * {F_{1}}_{cat} + W_{dog} * {F_{1}}_{dog} + W_{bird} * {F_{1}}_{bird} F1Weighted−average=Wcat∗F1cat+Wdog∗F1dog+Wbird∗F1bird
= 0.3 ∗ 0.69 + 0.3 ∗ 0.75 + 0.4 ∗ 0.872 = 0.781 = 0.3 * 0.69+ 0.3 * 0.75+ 0.4 * 0.872=0.781 =0.3∗0.69+0.3∗0.75+0.4∗0.872=0.781
使用scikit-learn包进行代码验证:
# 加权平均方法
P_Weighted_average = precision_score(y_true, y_pred, average="weighted")
R_Weighted_average = recall_score(y_true, y_pred, average="weighted")
F1_Weighted_average = f1_score(y_true, y_pred, average="weighted")
print("Base Weighted_average method, the precision is {}, recall is {}, and f1_score is {}".format(P_Weighted_average, R_Weighted_average, F1_Weighted_average))
结果展示如下(由于个人计算时,选择多次近似的原因,可能在小数位上略有不同):

3.3.3 微平均(Micro-average)方法
与宏平均方法和加权平均方法不同的是,微平均方法直接统计所有类别的TP,FP,FN的和,然后统一计算。
举例如下:
假设有三个类别,分别是猫,狗,鸟,一共50个样本, 其中猫15只,狗15只,鸟20只。模型预测结果如下图所示,现在要计算全部类别的Precision和Recall。

对于猫而言,
T P c a t = 10 , F P c a t = 2 + 2 = 4 , F N c a t = 4 + 1 = 5 TP_{cat}=10, \quad FP_{cat}=2+2=4, \quad FN_{cat}=4+1=5 TPcat=10,FPcat=2+2=4,FNcat=4+1=5
对于狗而言,
T P d o g = 12 , F P d o g = 4 + 1 = 5 , F N d o g = 2 + 1 = 3 TP_{dog}=12, \quad FP_{dog}=4+1=5, \quad FN_{dog}=2+1=3 TPdog=12,FPdog=4+1=5,FNdog=2+1=3
对于鸟而言,
T P b i r d = 17 , F P b i r d = 1 + 1 = 2 , F N b i r d = 2 + 1 = 3 TP_{bird}=17, \quad FP_{bird}=1+1=2, \quad FN_{bird}=2+1=3 TPbird=17,FPbird=1+1=2,FNbird=2+1=3
则,微平均方法的Precision和Recall。如下:
P M i c r o − a v e r a g e = T P c a t + T P d o g + T P b i r d T P c a t + T P d o g + T P b i r d + F P c a t + F P d o g + F P b i r d P_{Micro-average} = \frac{TP_{cat} + TP_{dog} + TP_{bird}}{TP_{cat} + TP_{dog} + TP_{bird} + FP_{cat} + FP_{dog} + FP_{bird}} PMicro−average=TPcat+TPdog+TPbird+FPcat+FPdog+FPbirdTPcat+TPdog+TPbird
= 10 + 12 + 17 10 + 12 + 17 + 4 + 5 + 2 = 39 50 = 0.78 = \frac{10+12+17}{10+12+17 + 4 + 5 + 2} = \frac{39}{50} = 0.78 =10+12+17+4+5+210+12+17=5039=0.78
R M i c r o − a v e r a g e = T P c a t + T P d o g + T P b i r d T P c a t + T P d o g + T P b i r d + F N c a t + F N d o g + F N b i r d R_{Micro-average} = \frac{TP_{cat} + TP_{dog} + TP_{bird}}{TP_{cat} + TP_{dog} + TP_{bird} + FN_{cat} + FN_{dog} + FN_{bird}} RMicro−average=TPcat+TPdog+TPbird+FNcat+FNdog+FNbirdTPcat+TPdog+TPbird
= 10 + 12 + 17 10 + 12 + 17 + 5 + 3 + 3 = 39 50 = 0.78 = \frac{10+12+17}{10+12+17 + 5 + 3 + 3} = \frac{39}{50} = 0.78 =10+12+17+5+3+310+12+17=5039=0.78
F 1 M i c r o − a v e r a g e = 2 ∗ P M i c r o − a v e r a g e ∗ R M i c r o − a v e r a g e P M i c r o − a v e r a g e + R M i c r o − a v e r a g e {F_{1}}_{Micro-average} = \frac{2 * P_{Micro-average} * R_{Micro-average} }{ P_{Micro-average} + R_{Micro-average}} F1Micro−average=PMicro−average+RMicro−average2∗PMicro−average∗RMicro−average
= 2 ∗ 0.78 ∗ 0.78 0.78 + 0.78 = 0.78 = \frac{2 * 0.78 * 0.78}{0.78 + 0.78} = 0.78 =0.78+0.782∗0.78∗0.78=0.78
可以发现, P M i c r o − a v e r a g e = R M i c r o − a v e r a g e = A c c u r a c y = F 1 M i c r o − a v e r a g e P_{Micro-average} = R_{Micro-average}= Accuracy = {F_{1}}_{Micro-average} PMicro−average=RMicro−average=Accuracy=F1Micro−average,这种情况从上式就可以分析出来原因。由于 F P c a t + F P d o g + F P b i r d = F N c a t + F N d o g + F N b i r d FP_{cat} + FP_{dog} + FP_{bird} = FN_{cat} + FN_{dog} + FN_{bird} FPcat+FPdog+FPbird=FNcat+FNdog+FNbird导致的。这也很好理解,当猫被预测为狗,在猫类别下,这是FN,但是在狗类别下,则是FP。并且,分母之和为全部样本数据量,分子为所有预测对的数量,其结果刚好也等于Accuracy的结果。
因此可以得出结论:
P M i c r o − a v e r a g e = R M i c r o − a v e r a g e = F 1 M i c r o − a v e r a g e = A c c u r a c y P_{Micro-average} = R_{Micro-average}={F_{1}}_{Micro-average}= Accuracy PMicro−average=RMicro−average=F1Micro−average=Accuracy
使用scikit-learn包进行代码验证:
# 微平均方法
P_Micro_average = precision_score(y_true, y_pred, average="micro")
R_Micro_average = recall_score(y_true, y_pred, average="micro")
F1_Micro_average = f1_score(y_true, y_pred, average="micro")
print("Base Micro_average method, the precision is {}, recall is {}, and f1_score is {}".format(P_Micro_average, R_Micro_average, F1_Micro_average))
# 准确率
acc = accuracy_score(y_true, y_pred)
print("Base accuracy method, the accuracy is {}".format(acc))
3.3.4 讨论
- 微平均方法和Accuracy结果一样,那么微平均方法的是否还有存在的必要?
我的理解是,微平均算法和Accuracy其实是一种指标,都是基于全部样本(不考虑类别)进行计算指标。此时,样本很容易受到类别不平衡的影响。相反,宏平局和加权平均都基于样本类别(考虑类别)计算指标的。不管是基于全部样本还是基于类别,这都是要根据实际应用场景来选择的。如果您有其他理解,欢迎评论区告诉我。
- 宏平均和加权平均的应用场景。
我的理解是,宏平局和加权平均都是基于样本类别(考虑类别)计算指标的。但是,考虑的方式不同。宏平局方法会受到稀有类别的影响,加权平均方法会受到主要类别影响。此时需要考虑应用场景的具体侧重来选择计算方法。当然如果,类别不平衡影响较大,则最好的方法还是调整样本数据,其次是loss计算方法。
4. P-R曲线、AP和mAP
4.1 P-R曲线
P-R曲线(Precision-Recall curve),是用来描述模型综合性能的一种指标。该曲线通过设置不同的置信度阈值,来计算不同阈值下的Precision值和Recall值,然后我们以横轴为Recall,纵轴为Precision绘制而成。如下图所示(图片来自西瓜书):
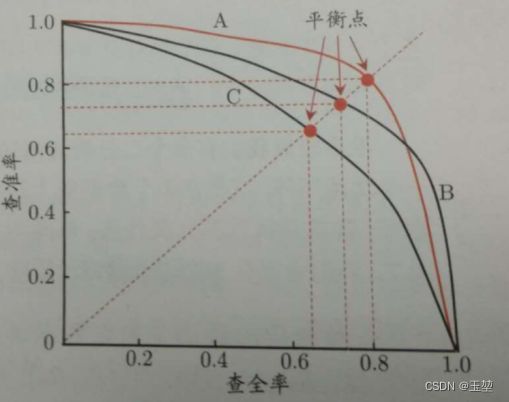
如果一个模型的P-R曲线可以包含另一个模型的P-R曲线的话,那么包含的模型就优于被包含的模型。如上图中模型A和模型B就优于模型C。但是在日常生活中最常见的还是P-R曲线相互交叉的情况,如上图的模型A和模型B,此时可以通过查看平衡点(Break-Even Pont,简称 BEP)或者 F 1 F_{1} F1-score。 F 1 F_{1} F1-score之前我们介绍过,这里就介绍下平衡点。平衡点就是在Precision和Recall相等时,P-R曲线上的值。平衡点越大,则说明模型效果越好。在上图中模型A就优于模型B。
总结:
- Precision和Recall是一对矛盾的指标。Precision降低,则Recall增加。
- 当阈值设定为最高时,亦即所有样本都被预测为反例,没有样本被预测为正例,此时在查准率 P r e c i s i o n = T P T P + F P Precision = \frac{TP}{ TP + FP} Precision=TP+FPTP算式中的 TP = 0, FP=0,所以 Precision没有意义。
同时在查全率算式中, R e c a l l = T P T P + F N Recall= \frac{TP}{TP + FN } Recall=TP+FNTP算式中的 TP = 0,所以Recall= 0%。
从而得出:当阈值设定为最高时,在P-R曲线上没有值。- 当阈值设定为最低时,亦即所有样本都被预测为正例,没有样本被预测为反例,此时在查准率 P r e c i s i o n = T P T P + F P Precision = \frac{TP}{ TP+ FP} Precision=TP+FPTP算式中 TP+ FP=全部样本,Precision = 正例在样本中的比例。
同时在查全率 R e c a l l = T P T P + F N Recall= \frac{TP}{TP + FN } Recall=TP+FNTP算式中的 FN = 0,所以 Recall=100%
从而得出2点结论:
(1)当阈值设定为最低时,得出P-R曲线上点的坐标为(1,正例占比)。
(2)P-R曲线中的不过(1,0)点。- TN和FN随著阈值调低而减少(或持平),TP和FP随著阈值调低而增加(或持平)。
从而得出:随着阈值的降低,FP增加,Precision会降低,同时FN减少,Recall会增加。因此,P-R曲线是一个从高往低的递减曲线。整体形状上图相似,但是曲线不过(1,0)点。- 当预测出来的全是TP时,Precision = Recall = 1。在P-R曲线中为(1,1)点。但是一般都很难达到。
- 提前补充一点,相比于P-R曲线,ROC曲线一定是从(0,0)到(1,1)的一条曲线。
还有另一种比较性能的方法就是计算P-R曲线下的面积,来评估模型的性能。此时P-R曲线下的面积就是AP(average precision)。即AP值越高则模型性能越好。(此处AP是针对单类别的,如果是多类别的话则是mAP指标)
补充说明2点:
- 西瓜书计算P-R曲线的方法不是提前设立置信度阈值,而是通过置信度将预测样本从大到小排序,然后依次将每个样本视为正例,来计算不同情况下的Precision和Recall值。最后绘制成P-R曲线。这种方法和上面说的卡置信度阈值其实是一种意思,不过卡阈值在样本量很大的情况下,可以少计算一些。后面附录中yolov5计算指标代码就是使用的西瓜书方法。
- 在目标检测中,我认为这个阈值是置信度阈值(判断正例反例的),而不是IoU阈值(判断预测正确与否)。在计算P-R曲线时,IoU阈值是固定的。
TODO:举例说明如下:
4.2 AP和mAP
P-R曲线下的面积即为AP( Average Precision ),是用来衡量单类别的模型平均准确度。通常用如下公式进行计算:
A P = ∫ 0 1 p ( r ) d r AP=\int_{0}^{1} p(r) dr AP=∫01p(r)dr
对于离散的P-R曲线,则使用近似的方式来计算,公式如下:
A P = ∑ n = 1 n p ( r n + 1 ) ( r n + 1 − r n ) AP=\sum_{n=1}^{n} p(r_{n+1})(r_{n+1}-r_{n}) AP=n=1∑np(rn+1)(rn+1−rn)
如下图所示:
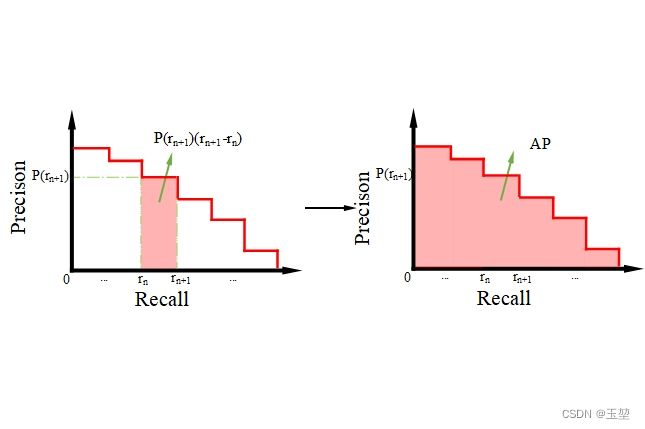
值得注意的是AP都是在一个默认IoU阈值下计算的。
附录中yolov5计算指标代码中使用函数np.trapz实现(梯度法)。但是该梯度法不是上面介绍近似方法。而是使用计算梯度面积公式来计算。具体可以参考作者:满船清梦压星河HK【python numpy】a.cumsum()、np.interp()、np.maximum.accumulate()、np.trapz()的介绍。。
如果是多类别的情况下,则使用mAP(mean Average Precision)来衡量模型性能。计算方法为将多个AP值累加后求平均。公式如下:
m A P = 1 k ∑ k = 1 n A P k mAP=\frac{1}{k}\sum_{k=1}^{n} AP_{k} mAP=k1k=1∑nAPk
其中k为类别数量。如果k=1,则AP=mAP。
4.3 yolo中[email protected]与[email protected]:0.95的含义
- [email protected]:将IoU阈值设为0.5时,计算每一类的所有图片的AP,然后所有类别求平均。
- [email protected]:0.95:表示在不同IoU阈值(从0.5到0.95,步长0.05)(0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95)下mAP的平均值。
- AP50,AP60,AP70…指的是取IoU阈值大于0.5,大于0.6,大于0.7…时的AP值。
5. ROC曲线和AUC
5.1 TPR、FPR、FNR和TNR
在学习ROC曲线之前,先得了解什么是TPR,FPR。顺便,也介绍下FNR,TNR。
TPR(True Positive Rate)真正率,用来表述在所有的正例中,预测为正例且正确的占比。即和Recall一样。公式如下:
T P R = T P T P + F N TPR =\frac{TP}{TP+FN} TPR=TP+FNTP
分母表示样本中所有的正例。
FPR(True Positive Rate)假正率,用来表述在所有的反例中,预测为正例(预测错误)的占比。公式如下:
F P R = F P F P + T N FPR =\frac{FP}{FP+TN} FPR=FP+TNFP
分母表示样本中所有的反例。
FNR(False Negative Rate)假反率,用来表述在所有的正例中,预测为反例(预测错误)的占比。公式如下:
F N R = F N T P + F N FNR =\frac{FN}{TP+FN} FNR=TP+FNFN
分母表示样本中所有的正例。
TNR(True Negative Rate)真反率,用来表述在所有的反例中,预测为反例且正确的占比。公式如下:
T N R = T N F P + T N TNR =\frac{TN}{FP+TN} TNR=FP+TNTN
分母表示样本中所有的反例。
5.2 ROC曲线的定义
ROC曲线(Receiver operating characteristic curve),中文又称接收者操作特征曲线。该曲线也是用来描述模型综合性能的指标,该曲线通过设置不同的置信度阈值,来计算不同阈值下的FPR值和TPR值,然后再以横轴为FPR,纵轴为TPR来绘制而成。如下图所示(图片来自西瓜书):
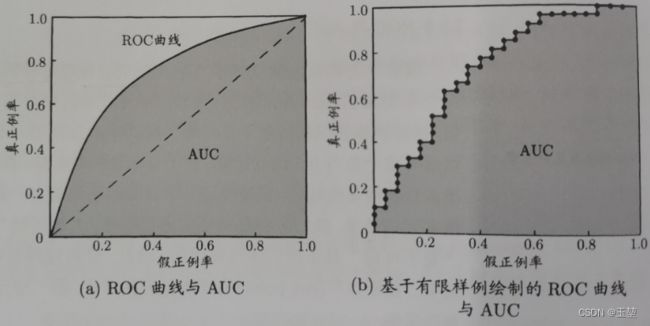
在ROC曲线上,越靠近左上角的点,效果越好。但是一般常用ROC曲线下的面积作为评判模型好坏的一种标准,而ROC曲线下的面积,也称AUC(Area Under Curve)。AUC越大,则表示模型综合性能越好。
总结(内容来自 维基百科:ROC曲线):
- 当阈值设定为最高时,亦即所有样本都被预测为反例,没有样本被预测为正例,此时在假反率 F P R = F P F P + T N FPR = \frac{FP}{ FP + TN } FPR=FP+TNFP算式中的 FP = 0,所以 FPR = 0%。同时在真正率(TPR)算式中, T P R = T P T P + F N TPR = \frac{TP }{TP + FN } TPR=TP+FNTP算式中的 TP = 0,所以 TPR = 0%。
从而得出:当阈值设定为最高时,必得出ROC坐标系左下角的点 (0, 0)。- 当阈值设定为最低时,亦即所有样本都被预测为正例,没有样本被预测为反例,此时在假正率 F P R = F P F P + T N FPR = \frac{FP}{ FP + TN} FPR=FP+TNFP算式中的 TN = 0,所以 FPR = 100%。同时在真正率 T P R = T P T P + F N TPR = \frac{TP}{ TP + FN} TPR=TP+FNTP算式中的 FN = 0,所以 TPR=100%
从而得出:当阈值设定为最低时,必得出ROC坐标系右上角的点 (1, 1)。- 因为TP、FP、TN、FN都是累积次数,TN和FN随著阈值调低而减少(或持平),TP和FP随著阈值调低而增加(或持平),所以FPR和TPR皆必随著阈值调低而增加(或持平)。
从而得出: 随著阈值调低,ROC点 往右上(或右/或上)移动,或不动;但绝不会往左下(或左/或下)移动
5.3 AUC
AUC(Area Under Curve)即指ROC曲线下的面积。有时不同分类算法的ROC曲线存在交叉,因此很多时候用AUC值作为算法好坏的评判标准。面积越大,表示分类性能越好。
计算方法同AP相似,此处就不做过多解释。
规律:
- 因为是在坐标系中1x1的方格里求面积,AUC必在0~1之间。
- 若随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之机率=AUC(下节会解释)。简单说就是AUC值越大的分类器,正确率越高。
- 从AUC判断分类器(预测模型)优劣的标准:
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。但在日常应用环境中,这是理想情况。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
5.4 P-R曲线和ROC曲线的区别
在作者:吴良超的学习笔记,ROC 曲线与 PR 曲线也给出了两点定理(文中论文链接为The Relationship Between Precision-Recall and ROC Curves):

既然P-R曲线和ROC曲线都是反应模型的综合性能。那么两者有什么区别呢,以下就是我的个人理解。可能有错误,希望读者朋友给与指导。
- 从ROC曲线上来讲,该曲线兼顾了正例(TPR)和反例(FPR)。ROC曲线更多的像是在反应模型的一种排序能力。因为随着阈值降低,预测正例的增多,TPR趋于稳定,FPR逐渐增加,表明模型更多的是在将正例和反例进行有效排序,将正例放在反例前面。即当将前面的TP全部预测到完后,TPR趋于稳定,FPR随着FP的增加,开始增加。
这是我对维基百科中这句话的解释:若随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之机率=AUC。
- 从P-R曲线上来讲,该曲线只关注正例(TP)的情况。从Precision和Recall的公式上也可以看出来。所以,模型不关注正例和反例的排序,只关心预测的准确性。
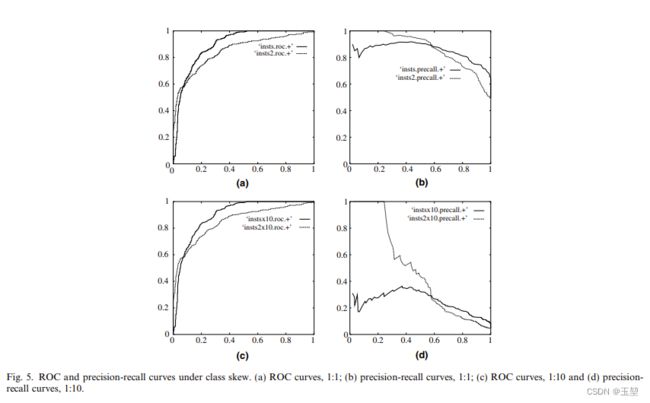
- 从上面两点可以看出,如果样本类别相对平衡的情况下,ROC曲线和P-R曲线相差不大,但是如果类别极度不平衡的情况下,P-R曲线就会展现很大的差异。如下图所示,图片来自论文An introduction to ROC analysis
下图中,两条线分别代表两个分类器。其中图a和图b分别表示在正负类别1:1的时候,ROC曲线和P-R曲线。图c和图d分别表示在正负类别1:10的时候,ROC曲线和P-R曲线。可见P-R曲线对类别不平衡的样本影响很大,无法较好反映模型效果。
- 从上面的例子可以看出,ROC曲线对于类别不平衡的情况不敏感,这是一种优点,可以很好的评估类别不平衡时的模型性能。但同时也是一种缺点。因为 ROC 曲线这种不变性无法很好的反应具体类别的对于整体性能的影响。在某些场景下,如果更关注正样本,这时候就需要用到 P-R 曲线了。
个人其实对这两种曲线的区别理解的不是很深,感觉解释也有点牵强。如果有懂的读者,可以在评论区指导我一下。
总结
本文内容可以总结为:
- IoU为交占比,其设置的阈值在目标检测中用来判断模型预测出的正例是正确(true)还是错误(False)。
- 置信度阈值,在目标检测中用来判断模型预测的是正例还是反例。大于置信度阈值的预测框全部都表示预测为正例(positive)。
- 目标检测没有TN这个概念。
- 目标检测FN指的是没有预测出来的目标。
- 目标检测中一个目标只能有一个TP,其他都是FP。
- 目标检测中FN和TP之和为GT。
- Precision着重评估:在预测为Positive的所有数据中,真实Positve的数据到底占多少?用来查准。
- Recall着重评估:在所有的Positive数据中,到底有多少数据被成功预测为Positive?,用来查全。
- F1-score既不是算数平均 P + R 2 \frac{P+R}{2} 2P+R,也不是几何平均 P R \sqrt{PR} PR,而是调和平均数 1 F 1 = 1 2 ( 1 P + 1 R ) \frac{1}{F_1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R}) F11=21(P1+R1),即 F 1 = 2 P R P + R F_{1} = \frac{2PR}{P + R} F1=P+R2PR。
- 多类别的Precision和Recall的计算方法有三种,宏平均,加权平均和微平均。其中宏平均受少数类别影响,加权平均受>多数类别影响。微平均一般不用。
- P-R曲线关注正例,容易受类别不平衡影响,当需要只关注正例的应用场景时,应该使用P-R曲线。
- ROC曲线既关注正例也关注反例,不受类别影响,可以应用在大多数的应用场景。
- P-R曲线和ROC曲线都是基于多个置信度阈值进行计算的。而不是IoU阈值。
- 计算P-R曲线,ROC曲线时需要提前设定IoU阈值。
- AP和AUC分别是P-R曲线和ROC曲线下的面积,并且都是值越大,模型性能越好。但是P-R曲线越靠近右上角,性能越好。ROC曲线越靠近左上角,性能越好。
写在最后,我没有想到这次文章能写这么长,2w多字了。内容上来了,但是文中的错误也会更多。俗话说当局者迷,旁观者清,所以如果读者朋友发现任何问题,可以在评论区及时指出,我会尽快修改。
最后如果您觉得对您有帮助的话,希望可以给小弟安排一个关注,点赞,收藏一条龙服务。
附录1 基于yolov5的计算指标代码,举例计算P-R曲线和ap值,mAP值。
还是之前的例子,为了后续计算,需要预测框坐标。因此,我通过labelimg2软件来进行标注。
注意,图上的iou值是我编的,请忽视。后面有计算出来的精确结果。

标注后的框为:
# class 0 = dog
# pred 的shape是(nx6), 其中第二维表示xmin,ymin,xmax,ymax, conf, class.
pred = torch.tensor([[6., 4., 192., 257., 0.97, 0.],
[9., 147., 129., 293., 0.71, 0.],
[229., 8., 309., 111., 0.26, 0.],
[201., 142., 285., 290., 0.41, 0.],
[319., 104., 450., 274., 0.98, 0.],
[345., 134., 459., 297., 0.88, 0.]])
# label 的shape是(nx5), 第二维表示class, xmin,ymin,xmax,ymax.
label = torch.tensor([[0., 15., 11., 213., 282.],
[0., 208., 30., 332., 282.],
[0., 312., 117., 437., 285.]])
整体代码:
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
import torch
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
# 代码包含的全部函数如下所示, 我重点解释的函数是compute_ap, ap_per_class。其他函数未作注释。
__all__= [
"plot_pr_curve", # 画p-r曲线的函数
"plot_mc_curve", # 画置信度下指标曲线的函数
"process_batch", # 生成tp矩阵,行代表预测框,列代表Iou阈值的数量。
"box_iou", # 计算iou值。
"compute_ap", # 计算ap值。
"ap_per_class", # main函数,计算整体的p,r,ap, f1
]
def plot_pr_curve(px, py, ap, save_dir='pr_curve.png', names=()):
# Precision-recall curve
fig, ax = plt.subplots(1, 1, figsize=(9, 6), tight_layout=True)
py = np.stack(py, axis=1)
if 0 < len(names) < 21: # display per-class legend if < 21 classes
for i, y in enumerate(py.T):
ax.plot(px, y, linewidth=1, label=f'{names[i]} {ap[i, 0]:.3f}') # plot(recall, precision)
else:
ax.plot(px, py, linewidth=1, color='grey') # plot(recall, precision)
ax.plot(px, py.mean(1), linewidth=3, color='blue', label='all classes %.3f [email protected]' % ap[:, 0].mean())
ax.set_xlabel('Recall')
ax.set_ylabel('Precision')
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
plt.legend(bbox_to_anchor=(1.04, 1), loc="upper left")
fig.savefig(Path(save_dir), dpi=250)
plt.close()
def plot_mc_curve(px, py, save_dir='mc_curve.png', names=(), xlabel='Confidence', ylabel='Metric'):
# Metric-confidence curve
fig, ax = plt.subplots(1, 1, figsize=(9, 6), tight_layout=True)
if 0 < len(names) < 21: # display per-class legend if < 21 classes
for i, y in enumerate(py):
ax.plot(px, y, linewidth=1, label=f'{names[i]}') # plot(confidence, metric)
else:
ax.plot(px, py.T, linewidth=1, color='grey') # plot(confidence, metric)
y = py.mean(0)
ax.plot(px, y, linewidth=3, color='blue', label=f'all classes {y.max():.2f} at {px[y.argmax()]:.3f}')
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
plt.legend(bbox_to_anchor=(1.04, 1), loc="upper left")
fig.savefig(Path(save_dir), dpi=250)
plt.close()
def process_batch(detections, labels, iouv):
"""
Return correct predictions matrix. Both sets of boxes are in (x1, y1, x2, y2) format.
Arguments:
detections (Array[N, 6]), x1, y1, x2, y2, conf, class
labels (Array[M, 5]), class, x1, y1, x2, y2
Returns:
correct (Array[N, 10]), for 10 IoU levels
"""
correct = torch.zeros(detections.shape[0], iouv.shape[0], dtype=torch.bool, device=iouv.device)
#iou 的shape是(真实框的数量, 预测框的数量.)
iou = box_iou(labels[:, 1:], detections[:, :4])
print("iou matix is : ", iou)
# 选出单类别的下的大于iou阈值的索引
x = torch.where(
(iou >= iouv[0]) & (labels[:, 0:1] == detections[:, 5])) # IoU above threshold and classes match
if x[0].shape[0]:
matches = torch.cat((torch.stack(x, 1), iou[x[0], x[1]][:, None]),
1).detach().cpu().numpy() # [label, detection, iou]
if x[0].shape[0] > 1:
matches = matches[matches[:, 2].argsort()[::-1]]
matches = matches[np.unique(matches[:, 1], return_index=True)[1]]
# matches = matches[matches[:, 2].argsort()[::-1]]
matches = matches[np.unique(matches[:, 0], return_index=True)[1]]
matches = torch.Tensor(matches).to(iouv.device)
correct[matches[:, 1].long()] = matches[:, 2:3] >= iouv
return correct
def box_iou(box1, box2):
# https://github.com/pytorch/vision/blob/master/torchvision/ops/boxes.py
"""
Return intersection-over-union (Jaccard index) of boxes.
Both sets of boxes are expected to be in (x1, y1, x2, y2) format.
Arguments:
box1 (Tensor[N, 4])
box2 (Tensor[M, 4])
Returns:
iou (Tensor[N, M]): the NxM matrix containing the pairwise
IoU values for every element in boxes1 and boxes2
"""
def box_area(box):
# box = 4xn
return (box[2] - box[0]) * (box[3] - box[1])
area1 = box_area(box1.T)
area2 = box_area(box2.T)
# inter(N,M) = (rb(N,M,2) - lt(N,M,2)).clamp(0).prod(2)
inter = (torch.min(box1[:, None, 2:], box2[:, 2:]) - torch.max(box1[:, None, :2], box2[:, :2])).clamp(0).prod(2)
return inter / (area1[:, None] + area2 - inter) # iou = inter / (area1 + area2 - inter)
def compute_ap(recall, precision):
""" Compute the average precision, given the recall and precision curves
# Arguments
recall: The recall curve (list) shape为(所有预测框的数量,)
precision: The precision curve (list) shape为(所有预测框的数量,)
# Returns
Average precision, precision curve, recall curve
"""
# Append sentinel values to beginning and end
# 在开头加个0,在结尾加个1。shape为(所有预测框的数量+2,)
mrec = np.concatenate(([0.0], recall, [1.0]))
# 由于recall是从小到大的,那么precision则是从大到小的。因此是开头加1,结尾加0.shape为(所有预测框的数量+2,)
mpre = np.concatenate(([1.0], precision, [0.0]))
# Compute the precision envelope
# np.maximum.accumulate:计算数组(或数组的特定轴)的累积最大值
# 举例:
# import numpy as np
# d = np.array([2, 0, 3, -4, -2, 7, 9])
# c = np.maximum.accumulate(d)
# print(c) # array([2, 2, 3, 3, 3, 7, 9])
# np.flip 数据反转,默认是axis=0,按行反转。
# 该语句的意思是,将mpre反转为从小到大,再计算累计最大值,再反转为从大到小。我的理解可能是让mpre更平滑。
mpre = np.flip(np.maximum.accumulate(np.flip(mpre)))
# Integrate area under curve
method = 'interp' # methods: 'continuous', 'interp'
if method == 'interp':
# 将0-1划分为101个点,即化成101个矩形。
x = np.linspace(0, 1, 101) # 101-point interp (COCO)
# np.trapz用于计算曲线下的面积,注意此时用的是梯形面积公式。
# 参考博客https://blog.csdn.net/qq_38253797/article/details/119706121
ap = np.trapz(np.interp(x, mrec, mpre), x) # integrate
else: # 'continuous'
i = np.where(mrec[1:] != mrec[:-1])[0] # points where x axis (recall) changes
ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1]) # area under curve
return ap, mpre, mrec
def ap_per_class(tp, conf, pred_cls, target_cls, plot=False, save_dir='./', names=(), eps=1e-16):
""" Compute the average precision, given the recall and precision curves.
Source: https://github.com/rafaelpadilla/Object-Detection-Metrics.
# Arguments
tp: True positives (nparray, nx1 or nx10). 里面都是bool值。shape为(所有预测框的数量 X iou阈值的数量)
conf: Objectness value from 0-1 (nparray). 里面都是置信度值。在0-1之间。shape为(所有预测框的数量,)
pred_cls: Predicted object classes (nparray). 里面都是预测框所预测的类别。shape为(所有框的数量,)
target_cls: True object classes (nparray). 里面都是真实框的所有类别。shape为(真实框的数量,),
plot: Plot precision-recall curve at [email protected]. 是否绘制在IoU阈值为0.5的P-R曲线。
save_dir: Plot save directory 图片保存路径。
names:为对应值和类别名,例如:(0:‘oiltanl’)
# Returns
The average precision as computed in py-faster-rcnn.
"""
# Sort by objectness
# 将置信度按照从大到小排序的索引。(argsort原本是从小到大排序,将conf变为-conf后即可得到,从大到小排序的索引)
i = np.argsort(-conf)
# 按照从大到小的索引,将tp,conf,pred_cls进行排序。(tp,conf,pred_cls每一行都是对应关系,对应一个预测框)
tp, conf, pred_cls = tp[i], conf[i], pred_cls[i]
# Find unique classes
# 获取整体唯一的真实类别,并统计每个类别的数量(return_counts=Ture,则返回每个类别的数量,存储在nt中。)
unique_classes, nt = np.unique(target_cls, return_counts=True)
# 全部真实类别的数量。
nc = unique_classes.shape[0] # number of classes, number of detections
# Create Precision-Recall curve and compute AP for each class
# px,py分别是绘制图像的横坐标值和纵坐标值。yolo作者通过将插值的方式(np.interp)获取recall从px的置信度阈值下的具体值。
# 该阈值(px)是可以自己设置的。
px, py = np.linspace(0, 1, 1000), [] # for plotting
# 初始化ap,p,r。
# 其中ap的shape为(真实类别数,iou阈值数:0.5,0.55...),
# p的shape为(真实类别的数量,1000:这是之前设置的置信度阈值数量)
# r的shape为(真实类别的数量,1000:这是之前设置的置信度阈值数量)
ap, p, r = np.zeros((nc, tp.shape[1])), np.zeros((nc, 1000)), np.zeros((nc, 1000))
# 开始计算每个类别下的指标
# ci表示索引,c表示具体真实类别值。
for ci, c in enumerate(unique_classes):
# 将pred_cls中等于当前类别的索引提取出来。
i = pred_cls == c
# n_l是当前类别下真实框的总数量
n_l = nt[ci] # number of labels
# n_p是当前类别下预测框的总数量
n_p = i.sum() # number of predictions
if n_p == 0 or n_l == 0:
continue
else:
# Accumulate FPs and TPs
# 这个是重点。
# tp是(所有框的数量 X iou阈值的数量),并且从大到小排序了。在tp中True,表示TP,False表示FP。
# cumsum(0)表示逐行累加。即第二行表示第一行和第二行的和。第三行表示第一行、第二行第三行的累加。最后的结果的shape还是(所有框的数量 X iou阈值的数量)
# 在进行相加时,true表示1,false表示0。经过cumsum(0)后,每一行都表示之前所有行的tp数量。
# 该方法相当于西瓜书中,逐个把每个样本都作为正例,来计算TP,FP。
# fpc, tpc的结果shape为(所有框的数量 X iou阈值的数量)。
# 其中fpc的每一行表示在当前行之前的所有预测框都为正例的情况下,fp的数量。每一列表示在该IoU阈值下,不同置信度阈值下的fp数量。
# 其中tpc的每一行表示在当前行之前的所有预测框都为正例的情况下,tp的数量。每一列表示在该IoU阈值下,不同置信度阈值下的tp数量。
# fpc = (1 - tp[i]).cumsum(0)
# 此处我单独跑的时候报错了,因为torch改版后不支持对bool直接进行'-'操作,因此改为'~'反转操作。结果是一样的
fpc = (~tp[i]).cumsum(0)
tpc = tp[i].cumsum(0)
# Recall
# R= TP/GT, n_l是所有真实框的数量,eps是怕分母为零,预先设置的极小值。shape为(所有框的数量 X iou阈值的数量)
recall = tpc / (n_l + eps) # recall curve
# 这个方法非常厉害,通过在一系列点集(-conf[i], recall[:, 0])生成的曲线下,以插值的方法计算在横坐标为-px时,对应的recall值。
# 这个方法通过插值可以随时修改对应的置信度阈值。
# 其中recall[:, 0],表示后续P-R曲线,f1指标是基于IoU阈值为0.5的前提下计算的,第一列为IoU阈值=0.5的情况。
r[ci] = np.interp(-px, -conf[i], recall[:, 0], left=0) # negative x, xp because xp decreases
# Precision
#原理同上。
precision = tpc / (tpc + fpc) # precision curve
p[ci] = np.interp(-px, -conf[i], precision[:, 0], left=1) # p at pr_score
# AP from recall-precision curve
# 开始计算不同iou阈值下的AP值。tp.shape[1]表示IoU阈值数量。
for j in range(tp.shape[1]):
# 通过compute_ap计算当前IoU阈值下,ap的值,其shape为真实类别的数量,1000:这是之前设置的置信度阈值数量
ap[ci, j], mpre, mrec = compute_ap(recall[:, j], precision[:, j])
# 如果要保存图片的话,则添加py的值.J=0表示仅在IoU阈值等于0.5时保存.
if plot and j == 0:
# py表示在mrec和mpre对应曲线上,插值出px对应的py值.
py.append(np.interp(px, mrec, mpre)) # precision at [email protected]
# Compute F1 (harmonic mean of precision and recall)
# 计算f1值,其shape为(真实类别的数量,1000:这是之前设置的置信度阈值数量)。
f1 = 2 * p * r / (p + r + eps)
# names原本为(标签值:标签名)
# 该语句判断标签值是否在unique_classes中
names = [v for k, v in names.items() if k in unique_classes] # list: only classes that have data
# 该语句按照顺序给类别名编号。
names = {i: v for i, v in enumerate(names)} # to dict
if plot:
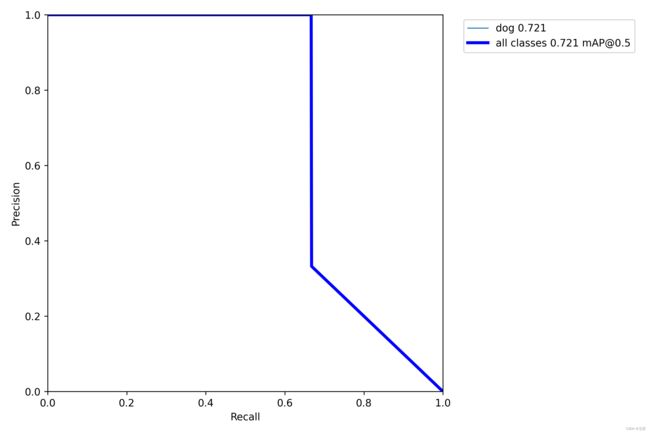
plot_pr_curve(px, py, ap, Path(save_dir) / 'PR_curve.png', names)
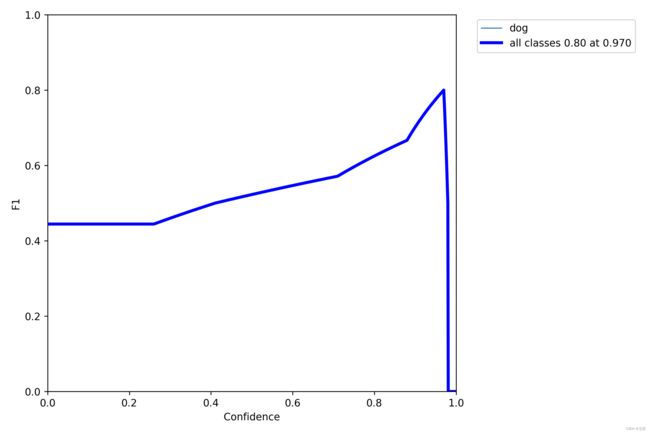
plot_mc_curve(px, f1, Path(save_dir) / 'F1_curve.png', names, ylabel='F1')
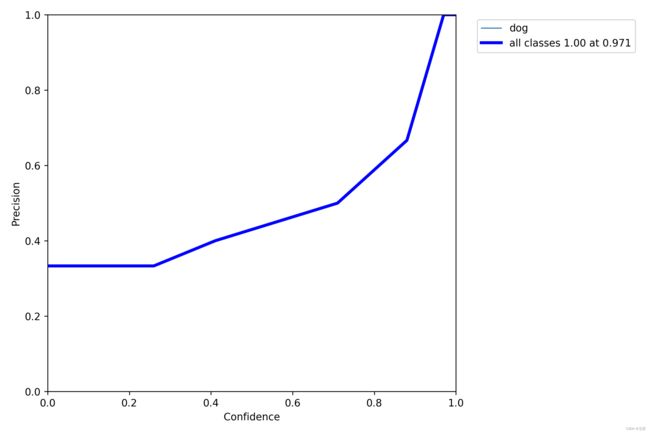
plot_mc_curve(px, p, Path(save_dir) / 'P_curve.png', names, ylabel='Precision')
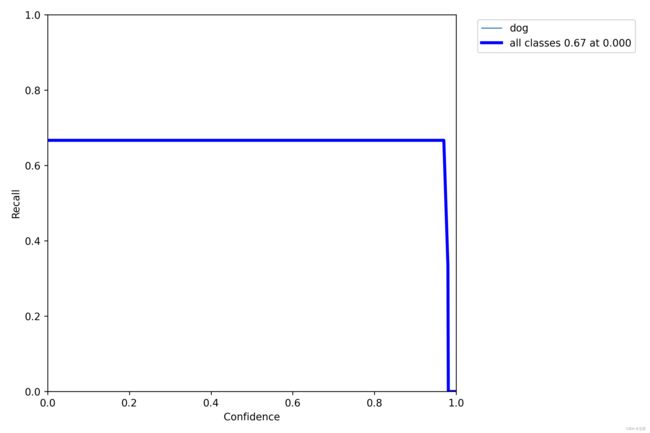
plot_mc_curve(px, r, Path(save_dir) / 'R_curve.png', names, ylabel='Recall')
# 其中f1为(真实类别的数量,1000:这是之前设置的置信度阈值数量),mean(0)表示按第一维数求平均,结果为(1, 1000)。argmax则是取出不同置信度下的最大值的索引。
# 此时可见,yolov5采用的是宏平均算法,把每个类别的f1加起来求平均,来求取最好的置信度阈值。
i = f1.mean(0).argmax() # max F1 index
# 根据最优置信度阈值下的结果。
# 此时 p, r, f1的shape都是(真实类别的数量,1)
p, r, f1 = p[:, i], r[:, i], f1[:, i]
# 反求出预测的tp和fp。
tp = (r * nt).round() # true positives
fp = (tp / (p + eps) - tp).round() # false positives
return tp, fp, p, r, f1, ap, unique_classes.astype('int32')
if __name__ == "__main__":
pred = torch.tensor([[6., 4., 192., 257., 0.97, 0.],
[9., 147., 129., 293., 0.71, 0.],
[229., 8., 309., 111., 0.26, 0.],
[201., 142., 285., 290., 0.41, 0.],
[319., 104., 450., 274., 0.98, 0.],
[345., 134., 459., 297., 0.88, 0.]])
label = torch.tensor([[0., 15., 11., 213., 282.],
[0., 208., 30., 332., 282.],
[0., 312., 117., 437., 285.]])
iouv = torch.tensor([[0.5]])
tp = process_batch(pred, label, iouv)
print("tp is : ", tp)
tp, fp, p, r, f1, ap, ap_class = ap_per_class(tp,
pred[:, 4],
pred[:, 5],
label[:, 0],
plot=True,
save_dir='./',
names={0:'dog'})
print("tp={}, fp={}, p={}, r={}, f1={}, ap={}, ap_class={} ".format(tp, fp, p, r, f1, ap, ap_class))
结果如下:
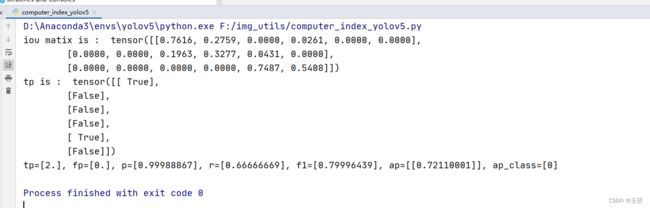
iou matrix 表示 3个真实框分别对6个预测框做iou计算。生成3x6的矩阵。
tp 表示将iou>0.5的情况下,每个预测框是否是tp。如果为tp,则是true,如果是fp,则是false。如果有多个IoU阈值,则有很多列。
生成的结果图:
注意
(1)计算ap时用的方法为梯度法,使用函数np.trapz实现。但是该梯度法不是本文介绍近似方法。具体可以参考作者:满船清梦压星河HK【python numpy】a.cumsum()、np.interp()、np.maximum.accumulate()、np.trapz()的介绍。
(2)在运行该代码时出现的错误:
- 错误: RuntimeError: Expected object of scalar type Long but got scalar type Float for sequence element 1 in sequence argument at position #1 ‘tensors’
代码位置:matches = torch.cat((torch.stack(x, 1), iou[x[0], x[1]][:, None]), 1).detach().cpu().numpy() # [label, detection, iou]
解决方法:一般进行操作的时候都是两个变量类型一样才可以,但是我从原本yolov5中拉下来代码也没修改,在服务器上也能运行。后来发现需要提高torch版本,原本torch1.2不支持int64和float32进行cat。但是升级到torch1.7就可以了。 - 错误:AttributeError: module ‘backend_interagg’ has no attribute ‘FigureCanvas’
代码位置:fig, ax = plt.subplots(1, 1, figsize=(9, 6), tight_layout=True)
解决方法:将matplotlib从3.6.0降到3.5.0 - 错误:OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.
代码位置:无
解决方法:解决OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.报错问题 - 错误:{RuntimeError}Subtraction, the
-operator, with a bool tensor is not supported. If you are trying to invert a mask, use the~orlogical_not()operator instead.
代码位置:fpc = (1 - tp[i]).cumsum(0)
解决办法:因为torch改版后不支持对bool直接进行‘-’操作,因此改为‘~‘反转操作。即fpc = (~tp[i]).cumsum(0)