智能优化算法：孔雀优化算法-附代码

智能优化算法：孔雀优化算法

摘要：孔雀优化算法( Peafowl Optimization Algorithm, POA), 是由 Jingbo Wang 等于2022 年提出的一种群体智能优化算法。其灵感来源于孔雀的群体行为。

1.孔雀优化算法

POA 通过雄孔雀求偶、雌孔雀自适应接近雄孔雀、幼孔雀自适应搜索食物源和雄孔雀交互 ４ 种寻优机制完成迭代更新，以逐渐逼近问题最优解 ． 过程中，所有孔雀根据其适应度值的排序进行角色分配，具有最高适合度值的前 ５ 只为雄孔雀，剩下的前30％ 为雌孔雀，其余为幼孔雀 。

1.1 雄孔雀求偶

雄孔雀求偶. 雄孔雀的位置更新机制可描述为
$$\begin{array}{rl}{\mathbf{x}}_{\mathrm{c},1}& ={\mathbf{x}}_{\mathrm{c},1}(t)+R_{\mathrm{s}}\frac{{\mathbf{x}}_{\mathrm{r},1}}{\Vert {\mathbf{x}}_{\mathrm{r},1}\Vert }\\ {\mathbf{x}}_{\mathrm{c},n}& =\left\{\begin{array}{ll}{\mathbf{x}}_{\mathrm{c},\mathrm{N}}(t)+\sigma R_{\mathrm{s}}\frac{{\mathbf{x}}_{\mathrm{r},\mathrm{N}}}{\Vert {\mathbf{x}}_{\mathrm{r},\mathrm{N}}\Vert },& \text{ 若 }{r}_{\mathrm{N}}<\epsilon \\ {\mathbf{x}}_{\mathrm{c},\mathrm{N}}(t),& \text{ 否则 }\end{array}\right\}\end{array}$$
式中: ${\mathbf{x}}_{\mathrm{c},1}$ 和 ${\mathbf{x}}_{\mathrm{c},\mathrm{N}}$ 分别为第 1 只和第 $N$ 只雄孔雀的 位置, $N=2,3,4,5;\sigma$ 和 $\epsilon$ 为决定雄孔雀位置更新 的算子, 当 $N=2,3,4,5$ 时, $\sigma =1.5,2,3,5$ 且 $\epsilon =0.9,0.8,0.6,0.3;r_{\mathrm{N}}$ 为随机生成的实数; ${\mathbf{x}}_{\mathrm{r},1}$ 和 ${\mathbf{x}}_{\mathrm{r},\mathrm{N}}$ 为一组随机向量; $R_{\mathrm{s}}$ 为雄孔雀围绕食物源旋转 的半径, 有
$$\begin{array}{l}{\mathbf{x}}_{\mathrm{r}}=2\mathrm{rand}(1,\mathrm{Dim})-1\\ R_{\mathrm{s}}(t)=R_{\mathrm{s}0}-\left(R_{\mathrm{s}0}-0\right){\left(k/k_{\max }\right)}^{0.01}\\ R_{\mathrm{s}0}=C_{\mathrm{v}}\left(x_{\mathrm{ub}}-x_{\mathrm{lb}}\right)\end{array}\}$$
式中: Dim 为决策变量的数量; 0 表示孔雀绕圈旋转 的圆心; $k$ 和 $k_{\text{max }}$ 分别为当前迭代次数和最大迭代 次数; $R_{\mathrm{s}0}$ 为初始旋转半径; $C_{\mathrm{v}}$ 为雄孔雀旋转因子,设为 $0.2;x_{\mathrm{ub}}$ 和 $x_{\mathrm{lb}}$ 为决策变量的上下限。
在该机制下, 适应度值越高的雄孔雀围绕食物 源旋转的概率越大, 且绕圈半径越小, 因此更趋近于 局部最优解. 可见, 雄孔雀位置代表的决策变量解趋 近最优解的能力与其适应度值成正相关, 与绕圈半 径成负相关。

1.2 雌孔雀自适应接近雄孔雀

雌孔雀自适应接近雄孔雀. 其位置更新机制为

${\mathbf{x}}_{\mathrm{h}}={\mathbf{x}}_{\mathrm{h}}(t)+3\theta \left({\mathbf{x}}_{\mathrm{c},\mathrm{N}}-{\mathbf{x}}_{\mathrm{h}}(t)\right),$

若 $r_5\in A$ (28) 式中: ${\mathbf{x}}_{\mathrm{h}}$ 为雌孔雀的位置; $r_5$ 为 $[0,1]$ 范围内的随 机数; $A$ 为决定雌孔雀位置更新的算子, 当 $N=1$, $2,3,4,5$ 时, $A$ 分别为 $[0.6,1)、[0.4,0.6)、[0.2$, $0.4)、[0.1,0.2)、[0,0.1)$; $\theta$ 为平衡雌孔雀局部探 索和全局搜索的算子, 有
$$\theta ={\theta }_0+\left({\theta }_1-{\theta }_0\right)k/k_{\max }$$
式中: ${\theta }_0=0.1、{\theta }_1=1$.
在该机制下, 当 $\theta <1/3$ 时 (迭代初期), 雌孔雀 趋向于所选择的雄孔雀, 进行局部勘测; 当 $\theta >1/3$ 时 (迭代中后期), 雌孔雀倾于向所选雄孔雀相对的 位置移动, 进行全局搜索. 因此, 较小的 $\theta$ 值有利于 雌孔雀在局部勘测过程中寻找高质量的决策变量 解; 较大的 $\theta$ 值有利于增强算法的随机性和全局搜 索能力, 避免陷人局部最优.

1.3 幼孔雀自适应搜索食物源

幼孔雀自适应搜索食物源. 幼孔雀向雄孔雀移 动的同时借助 Levy 飞行机制在搜索空间进行随机搜索:
$$\begin{array}{rl}{\mathbf{x}}_{\mathrm{cu}}=& {\mathbf{x}}_{\mathrm{cu}}(t)+\alpha \mathrm{Levy}\left({\mathbf{x}}_{\mathrm{c},1}(t)-{\mathbf{x}}_{\mathrm{cu}}(t)\right)+\\ & \beta \left({\mathbf{x}}_{\mathrm{pu}}(t)-{\mathbf{x}}_{\mathrm{cu}}(t)\right)\\ {\mathbf{x}}_{\mathrm{pu}}=& {\mathbf{x}}_{\mathrm{c},N}(t),r_6\in B\end{array}\}$$
式中: $x_{\mathrm{cu}}$ 和 $x_{\mathrm{pu}}$ 分别为幼孔雀位置和幼孔雀跟随的 雄孔雀位置; $r_6$ 为 $[0,1]$ 范围内的随机数; $B$ 为决定 幼孔雀位置更新的算子, 当 $N=1,2,3,4,5$ 时, $B$
分别为 $[0.8,1)、[0.6,0.8)、[0.4,0.6)、[0.2$, $0.4)、[0,0.2);\alpha$ 和 $\beta$ 为随迭代次数动态变化的算 子, 有
$$\begin{array}{l}\alpha ={\alpha }_0\left({\alpha }_0-{\alpha }_1\right){\left(k/k_{\max }\right)}^2\\ \beta ={\beta }_0+\left({\beta }_1-{\beta }_0\right){\left(k/k_{\max }\right)}^{0.5}\end{array}\}$$
式中 : ${\alpha }_0=0.9、{\alpha }_1=0.4、{\beta }_0=0.1、{\beta }_1=1$.
在该机制下,当 $\alpha >\beta$ 时 (迭代初期), 幼孔雀主 要进行随机搜索; 当 $\beta >\alpha$ 时 (迭代中后期), 幼孔雀 逐渐向 5 只雄孔雀收玫. 可见, $\alpha$ 和 $\beta$ 共同指导幼孔 雀的位置更新, 引导劣势解向最优解移动, 并加快收敛速度.

1.4 雄孔雀交互行为

雄孔雀交互行为. 拥有最佳食物源的第 1 只雄孔雀被视为领导者, 第 $2\sim 4$ 只雄孔雀逐渐向第 1 只雄孔雀移动:
$${\mathbf{x}}_{\mathrm{c},\mathrm{N}}={\mathbf{x}}_{\mathrm{c},\mathrm{N}}(t)+\theta {\mathbf{d}}_{\mathrm{N}}+r_N^{\prime }\frac{{\mathbf{D}}_{\mathrm{N}}}{\Vert {\mathbf{D}}_{\mathrm{N}}\Vert }$$
式中:
$$\begin{array}{rl}& {\mathbf{d}}_{\mathrm{N}}={\mathbf{x}}_{\mathrm{c},1}-{\mathbf{x}}_{\mathrm{c},\mathrm{N}}\\ & {\mathbf{D}}_{\mathrm{N}}={\mathbf{x}}_{\mathrm{r},\mathrm{N}}^{\prime }-\frac{{\mathbf{x}}_{\mathrm{r},\mathrm{N}}^{\prime }{\mathbf{d}}_{\mathrm{N}}}{{\mathbf{d}}_{\mathrm{N}}{\mathbf{d}}_{\mathrm{N}}}{\mathbf{d}}_{\mathrm{N}}\end{array}$$
$r_n^{\prime }$ 为 $[0,1]$ 范围内的随机数; ${\mathbf{x}}_{\mathrm{r},\mathrm{N}}^{\prime }$ 为随机向量。

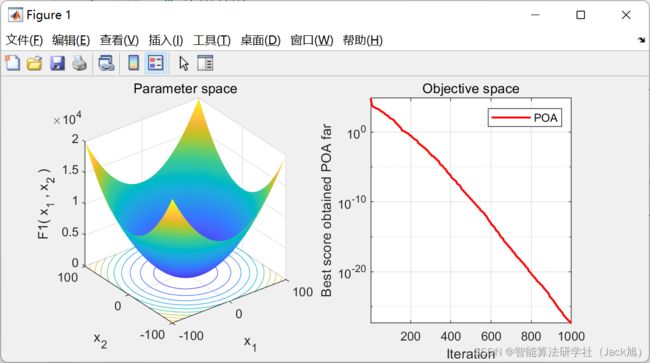
3.实验结果

4.参考文献

[1] Jingbo Wang, Bo Yang, Yijun Chen, Kaidi Zeng, Hao Zhang, Hongchun Shu, Yingtong Chen.Novel phasianidae inspired peafowl (Pavo muticus/cristatus) optimization algorithm: Design,evaluation, and SOFC models parameter estimation.Sustainable Energy Technologies and Assessments 2021,50:101825. https://doi.org/10.1016/j.seta.2021.101825

5.Matlab代码

6.python代码