【数据预测】基于matlab粒子群优化RBF神经网络数据预测【含Matlab源码 1755期】
一、粒子群优化RBF神经网络简介
1 粒子群优化算法
粒子群优化算法( PSO)是指通过模拟鸟群觅食的协作行为,实现群体最优化。PSO是一种并行计算的智能算法,其基本模型如下:
假设群体规模为M,在D维空间中,群体中的第i个个体表示为XD= ( xm1,xm2…xm D)T,速度表示为VD= ( vm1,vm2…vm D)T,位置( 代表在当前空间中搜索到的最佳点,即个体极值) 表示为PD= ( pm1,pm2…pm D)T,m = 1,2,…,M,将粒子个体的最小极值最为当前全局最优位置, 表示为Pg= ( pg1,pg2…pg D)T。速度与位置的更新公式[2]为:
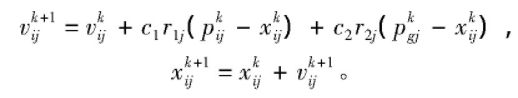
式中: i = 1,2,…M; j为粒子的第j维; k为迭代次数; c1与c2为加速度常数,分别用于调节粒子自身最佳位置和全局最佳位置的步长,一般在0 ~ 2 之间取值; r1与r2为在[0,1]区间分别的随机函数。为了减少搜索空间的可能性,通常要给粒子的速度设定范围,即vij∈[Vmin,Vmax]。
粒子群优化算法的流程如下:
- 初始化。设置种群相关初始化参数,包括种群数目M、迭代次数T、粒子速度与位置、速度范围。
- 计算粒子适应度。
- 更新个体极值。如果当前适应度值优于上次的迭代的值,那么则将当前值作为新的个体极值。
- 更新种群极值。
- 更新粒子的速度与位置。
- 判断。若满足设定的结束条件,则进行下一步,若不满足,则返回到步骤2。
- 结束。
2 RBF神经网络
径向神经网络( Radical Basis Function,RBF)是一种前馈神经经网络,具有计算速度快、最佳逼近及收敛能力强的优点。其拓扑结构如图3所示。

1 ) 输入层: 输入向量X = ( x1,x2…xI)T。该向量为输入数据标准化处理后所得。
2) 隐含层: 设隐含层节点数目为J,隐含层第j的神经元中心与宽度分别为cj和 σj,该神经元的输出为:

式中: ‖·‖ 为欧几里得距离; φ(·) 为径向基函数。常用的基函数见表1。
表1 径向基函数

4) 输出层:

其中wjk为连接权值。
3 基于粒子群优化的RBF神经网络预测方法
由于RBF神经网络具有最佳逼近的能力,而粒子群优化算法的收敛能力较强,因此,本文将2 种算法进行结合,即用粒子群优化算法优化RBF神经网络中的参数,算法流程如图4 所示。
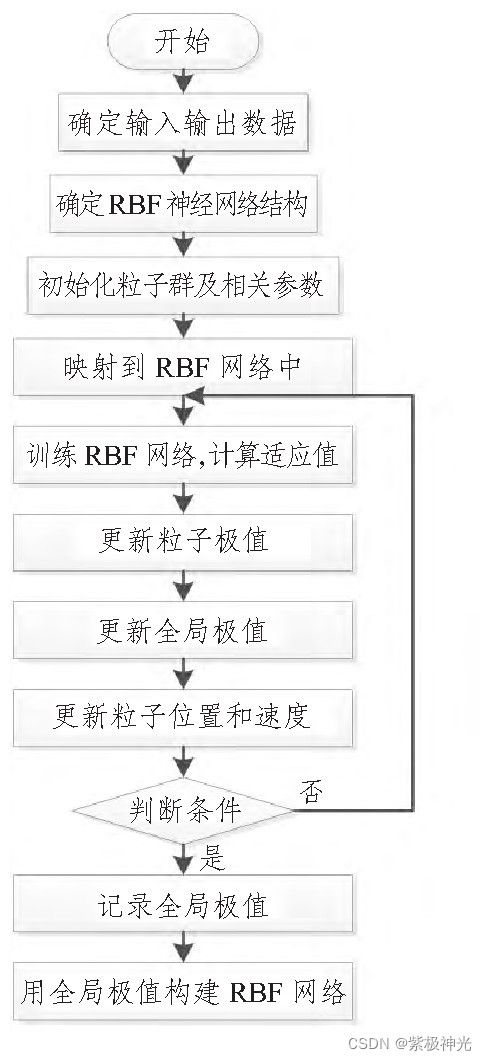
图4 流程图
由RBF神经网络模型相关参数构成粒子的向量,在每次迭代后,将得到的粒子极值映射到RBF网络中,并将RBF神经网络的误差函数作为粒子群优化过程中的适应度函数,计算方法为:
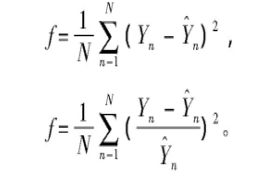
式中: Yn为RBF神经网络的输出值;^Yn为实际值; N为样本总数。
二、部分源代码
clc;
clear;
tic;
SamNum=48; %训练样本数
TargetSamNum=3; %测试样本数
InDim=1; %样本输入维数
UnitNum=2; %隐节点数
MaxEpoch=1200; %最大训练次数
num=2;%对应四个特征
%E0=0.2; %目标误差
gbesthistory=[];
% 根据目标函数获得样本输入输出(训练样本)
rand('state',sum(100*clock));
%NoiseVar=0.0005;
%Noise=NoiseVar*randn(1,SamNum);
load data
%归一化
data1=data';
data=mapminmax(data1,0,1);
data=data';
%建立训练集测试集
x_train=[data(1:48,1).';data(1:48,2).';data(1:48,3).';data(1:48,4).'];
x_test=[data(2:49,num).'];
y_train=[data(49:51,1).';data(49:51,2).';data(49:51,3).';data(49:51,4).'];
y_test=[data(50:52,num).'];
SamIn=x_train;
SamOut=x_test;
%测试样本
TargetIn=y_train;
TargetOut=y_test;
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;
popcount=50; %粒子数
poplength=6; %粒子维数
Wstart=0.9;%初始惯性权值
Wend=0.2;%迭代次数最大时惯性权值
%个体和速度最大最小值
Vmax=1;
Vmin=-1;
popmax=4;
popmin=-4;
%粒子位置速度和最优值初始化
for i=1:popcount
pop(i,:)=rand(1,9);%初始化粒子位置
V(i,:)=rand(1,9);%初始化粒子速度
%计算粒子适应度值
Center=pop(i,1:3);
SP=pop(i,4:6);
W=pop(i,7:9);
Distance=dist(Center',SamIn);
SPMat=repmat(SP',1,SamNum);%repmat具体作用
UnitOut=radbas(Distance./SPMat);%径向基函数
NetOut=W*UnitOut;%网络输出
Error=SamOut-NetOut;%网络误差
%SSE=sumsqr(Error);
%fitness(i)=SSE;
RMSE=sqrt(sumsqr(Error)/SamNum);
fitness(i)=RMSE;
%fitness(i)=fun(pop(i,:));
end
%适应度函数(适应度值为RBF网络均方差)
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);%全局最优值
pbest=pop;%个体最优值
pbestfitness=fitness;%个体最优适应度值
gbestfitness=bestfitness;%全局最优适应度值
%迭代寻优
for i=1:MaxEpoch
Vmax=1.00014^(-i);
Vmin=-1.00014^(-i);
for j=1:popcount
% if (fitness(j)Vmax))=Vmax;
V(j,find(V(j,:) 三、运行结果
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社,2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社,2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社,2018.
[6]韦波.粒子群优化的RBF神经网络在海上运输事故预测中的应用[J].舰船科学技术. 2016,38(04)

