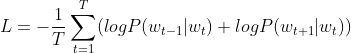【DL学习笔记10】《深度学习进阶——自然语言处理》——ch03: word2vec

 

目录

1. 基于推理的方法和神经网络

神经网络中单词的处理方法

2. 简单的word2vec

CBOW模型的推理与学习

3. 学习数据的准备

上下文和目标词

转化为one-hot表示

数据预处理总结

4. CBOW模型的实现

5. word2vec的补充说明

CBOW模型和概率

skip-gram模型

两个模型的区别分析

基于计数与基于推理总结

---

上章中，我们使用基于计数的方法得到单词的分布式表示，本章我们将讨论基于推理的方法，推理机制用的是神经网络，实现一个简单的word2vec。

1. 基于推理的方法和神经网络

• 区别：
  • 基于计数的方法在处理大规模语料库时会出现问题，因为它要生成所有单词的共现矩阵，再进行SVD获得单词的分布式表示
  • 基于推理的方法使用神经网络，通常在mini-batch数据上进行学习，因此可以处理大规模语料库，而且神经网络的学习可以使用多台机器、多个GPU并行执行，加速学习过程
• 基于推理的方法
  • 概要：输入上下文，模型输出各个单词的出现概率
  • 在这样的框架中，使用语料库来学习模型，使之能做出正确的预测。另外作为模型学习的产物，我们得到了单词的分布式表示

神经网络中单词的处理方法

• 神经网络无法直接处理单词，需要先将单词转化为固定长度的向量
• one-hot表示：准备元素个数与词汇个数相等的向量，并将单词ID对应的元素设为1，其它元素设为0
• 基于神经网络的全连接层的变换：输入层的各个神经元分别对应于7个单词，中间层的神经元暂为3个，另外本章使用的全连接层将省略偏置，相当于在计算矩阵乘积，MatMul层

# 输入数据c的维数是2，考虑了mini-batch处理
# 将各个数据保存在了第1维(0维度)，也就是行方向
c = np.array([[1, 0, 0, 0, 0, 0, 0]])
W = np.random.randn(7, 3)
layer = MatMul(W)
h = layer.forward(c)
print(h)

2. 简单的word2vec

• 我们使用由原版word2vec提出的名为continuous bag-of-words(CBOW)的模型作为神经网络
• word2vec最初指程序或工具，现在也指神经网络的模型，但是正确地说，CBOW模型和skip-gram模型是word2vec中使用的两个神经网络

CBOW模型的推理与学习

• CBOW模型是根据上下文预测目标词的神经网络。通过训练该模型，使其能尽可能地进行正确的预测，我们可以获得单词的分布式表示。模型的输入是上下文，用[’you’, ‘goodbye’]这样的单词列表表示，再将其转换为hot-one表示

• 分析：

  • 因为对上下文仅考虑两个单词，所以输入层有两个
  • 输入层到中间层是两个相同的全连接层，中间层到输出层是另一个全连接层
  • 中间层是两个输入层变换后的值的平均
  • 输出层有7个神经元，表示各个单词的得分，值越大说明出现概率越高
  • 对这些得分应用Softmax函数就可以得到概率
  • 全连接层的权重 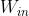就是我们要的单词的分布式表示。通过反复学习，不断更新各个单词的分布式表示，以正确的从上下文预测出应当出现的单词

• 实现：

# 样本的上下文数据
c0 = np.array([[1, 0, 0, 0, 0, 0, 0]])
c1 = np.array([[0, 0, 1, 0, 0, 0, 0]])

# 权重的初始值
W_in = np.random.randn(7, 3)
W_out = np.random.randn(3, 7)

# 生成层
in_layer0 = MatMul(W_in)
in_layer1 = MatMul(W_in)
out_layer = MatMul(W_out)

# 正向传播
h0 = in_layer0.forward(c0)
h1 = in_layer1.forward(c1)
h = 0.5 * (h0 + h1)
s = out_layer.forward(h)

print(s)
# [[ 0.6819715  -0.08929536 -1.68627624  0.8961376  
# -1.03090686 -0.65943828 0.80935793]]

• CBOW模型的学习：调整权重，使预测准确。其结果是权重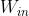学习到蕴含单词出现模式的向量
  • 我们处理的模型是一个进行多类别分类的神经网络，因此先使用Softmax函数将得分转化为概率，然后求这些概率和监督标签之间的交叉熵误差，并将其作为损失进行学习
  • 所以我们只需要在推理的模型上加上Softmax with loss层就可以了

3. 学习数据的准备

我们仍以“You say goodbye and I say hello.”作为语料库

上下文和目标词

• word2vec中使用的神经网络的输入是上下文，它的正确解标签是被这些上下文包围在中间的单词，即目标词
• 接下来我们的目标就是从corpus(语料库)中提取出contexts(上下文)和target(目标词)。其中contexts是二维数组，第0维保存的是各个上下文数据。
• 实现:

def create_contexts_target(corpus, window_size=1):
    '''生成上下文和目标词

    :param corpus: 语料库（单词ID列表）
    :param window_size: 窗口大小（当窗口大小为1时，左右各1个单词为上下文）
    :return:
    '''
    target = corpus[window_size:-window_size]
    contexts = []

    for idx in range(window_size, len(corpus)-window_size):
        cs = []
        for t in range(-window_size, window_size + 1):
            if t == 0:
                continue
            cs.append(corpus[idx + t])
        contexts.append(cs)

    return np.array(contexts), np.array(target)

转化为one-hot表示

• 使用单词ID时的contexts的形状是（6，3），转化为one-hot表示后，形状变为（6， 2， 7）
• 实现：

def convert_one_hot(corpus, vocab_size):
    '''转换为one-hot表示

    :param corpus: 单词ID列表（一维或二维的NumPy数组）
    :param vocab_size: 词汇个数
    :return: one-hot表示（二维或三维的NumPy数组）
    '''
    N = corpus.shape[0]

    if corpus.ndim == 1:
        one_hot = np.zeros((N, vocab_size), dtype=np.int32)
        for idx, word_id in enumerate(corpus):
            one_hot[idx, word_id] = 1

    elif corpus.ndim == 2:
        C = corpus.shape[1]
        one_hot = np.zeros((N, C, vocab_size), dtype=np.int32)
        for idx_0, word_ids in enumerate(corpus):
            for idx_1, word_id in enumerate(word_ids):
                one_hot[idx_0, idx_1, word_id] = 1

    return one_hot

数据预处理总结

text = 'You say goodbye and I say hello.'

# 1.生成单词ID列表以及字典
corpus, word_to_id, id_to_word = preprocess(text)
# 2.生成上下文和目标词
contexts, target = create_contexts_target(corpus, window_size=1)
# 3.转化为one-hot表示
vocab_size = len(word_to_id)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)

4. CBOW模型的实现

class SimpleCBOW:
    def __init__(self, vocab_size, hidden_size):
        V, H = vocab_size, hidden_size

        # 初始化权重，astype('f')指定权重数据类型为32位浮点数
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(H, V).astype('f')

        # 生成层
        self.in_layer0 = MatMul(W_in)
        self.in_layer1 = MatMul(W_in)
        self.out_layer = MatMul(W_out)
        self.loss_layer = SoftmaxWithLoss()

        # 将所有的权重和梯度整理到列表中
        layers = [self.in_layer0, self.in_layer1, self.out_layer]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 将单词的分布式表示设置为成员变量
        self.word_vecs = W_in

    def forward(self, contexts, target):
        h0 = self.in_layer0.forward(contexts[:, 0])
        h1 = self.in_layer1.forward(contexts[:, 1])
        h = (h0 + h1) * 0.5
        score = self.out_layer.forward(h)
        loss = self.loss_layer.forward(score, target)
        return loss

    def backward(self, dout=1):
        ds = self.loss_layer.backward(dout)
        da = self.out_layer.backward(ds)
        da *= 0.5
        self.in_layer1.backward(da)
        self.in_layer0.backward(da)
        return None

• 初始化中，由于多个层共享相同的权重，params列表中存在多个相同的权重，在这种情况下，Adam、Momentum等优化器的运行会变得不符合预期，为此在Trainer类的内部，在更新参数时，会进行简单的去重操作
• 因此通过先调用forward( )函数，再调用backward( )函数，grads列表中的梯度被更新。下面我们使用上面实现的SimpleCBOW类进行学习
• 和一般的神经网络的学习完全相同，首先准备好学习数据，然后求梯度，并逐步更新权重参数

window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)

vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)

model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)
trainer.fit(contexts, target, max_epoch, batch_size)
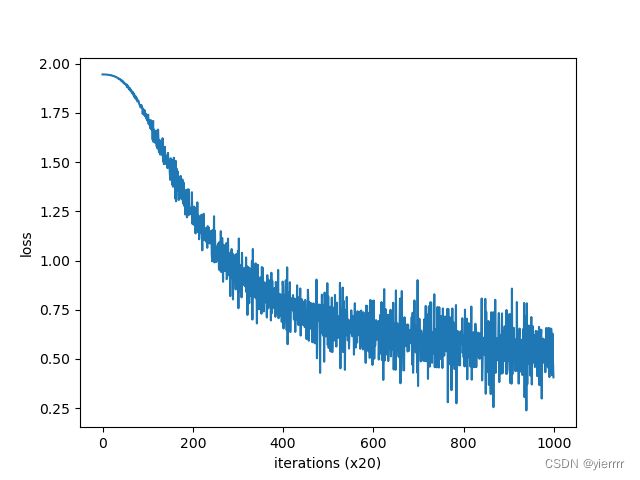
trainer.plot()

 

• 查看保存了权重的成员变量word_vecs

word_vecs = model.word_vecs
for word_id, word in id_to_word.items():
    print(word, word_vecs[word_id])

""" 结果如下

you [ 0.9532905 -1.3833157  0.9600834 -1.333352   0.8822044]
say [-1.1779003  -0.48005727 -1.1771895   0.18510178 -1.1754793 ]
goodbye [ 0.91159654 -0.50769854  0.9059445  -0.55956     0.9156929 ]
and [-0.8856774 -1.7152286 -0.8718644  1.4566529 -0.884314 ]
i [ 0.9017562  -0.49907902  0.911299   -0.55395776  0.9301149 ]
hello [ 0.94429344 -1.4025779   0.95916694 -1.3244895   0.89125985]
. [-1.1089147  1.4758974 -1.1068727 -1.4950483 -1.1257972]
"""

5. word2vec的补充说明

CBOW模型和概率

• 对于第t个单词，考虑窗口大小为1的上下文的CBOW模型来说，给定上下文$w_{t-1}$和$w_{t+1}$时目标词$w_t$的概率，用后验概率表示为：
• 使用后验概率就可以简洁的表示交叉熵误差函数为：

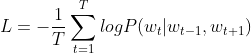
skip-gram模型

skip-gram模型是反转了CBOW模型处理的上下文和目标词的模型，从中间的单词（目标词）预测周围的多个单词（上下文）

 

• 输入层只有一个，输出层的数量与上下文的单词个数相等。因此首先要分别求出各个输出层的损失，然后求和为最后的损失

• 同样的，用后验概率可以表示为：

• 损失函数可以表示为：

class SimpleSkipGram:
    def __init__(self, vocab_size, hidden_size):
        V, H = vocab_size, hidden_size

        # 初始化权重
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(H, V).astype('f')

        # 生成层
        self.in_layer = MatMul(W_in)
        self.out_layer = MatMul(W_out)
        self.loss_layer1 = SoftmaxWithLoss()
        self.loss_layer2 = SoftmaxWithLoss()

        # 将所有的权重和梯度整理到列表中
        layers = [self.in_layer, self.out_layer]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 将单词的分布式表示设置为成员变量
        self.word_vecs = W_in

    def forward(self, contexts, target):
        h = self.in_layer.forward(target)
        s = self.out_layer.forward(h)
        l1 = self.loss_layer1.forward(s, contexts[:, 0])
        l2 = self.loss_layer2.forward(s, contexts[:, 1])
        loss = l1 + l2
        return loss

    def backward(self, dout=1):
        dl1 = self.loss_layer1.backward(dout)
        dl2 = self.loss_layer2.backward(dout)
        ds = dl1 + dl2
        dh = self.out_layer.backward(ds)
        self.in_layer.backward(dh)
        return None

两个模型的区别分析

• 损失函数：skip-gram模型的预测次数和上下文单词数量一样多，所以它的损失函数需要求各个单词对于的损失的总和，而CBOW模型只需要求目标词的损失
• 学习速度：CBOW更快
• 分布式表示的准确度：大部分情况下skip-gram更好
  • 因为根据一个单词预测其周围的单词的难度是比根据上下文预测目标词难的，所以经过了更难的问题的锻炼，skip-gram模型能提供更好的单词的分布式表示

基于计数与基于推理总结

	基于计数	基于推理
学习机制	通过对整个语料库的统计数据进行一次学习来获得单词的分布式表示	反复观察语料库的一部分数据进行学习
添加新词并更新	从头重新计算，重新生成共现矩阵、进行SVD等操作	允许参数的增量学习，就是可以将之前学习到的权重作为下一次学习的初始值
分布式表示的性质	编码单词的相似性	除了单词的相似性外，还能理解更复杂的单词之间的模式
分布式表示的准确度	就单词的相似性而言，两种方法难分上下

• 在word2vec之后，提出了GloVe方法，融合了基于计数和推理，将整个语料库的统计数据的信息纳入损失函数，进行mini-batch学习