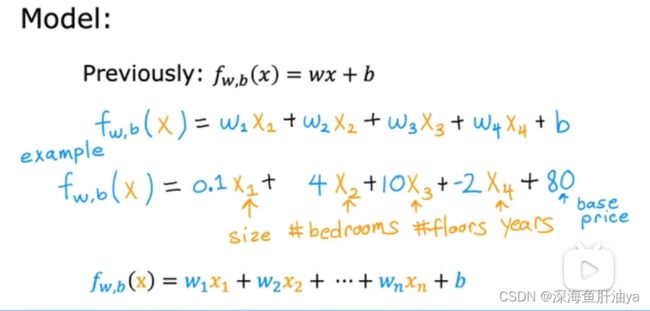向毕业妥协系列之机器学习笔记:监督学习-回归与分类（二）

目录

一.多维向量 

二.向量化

三.用于多元线性回归的梯度下降法

四.正规方程

五.特征缩放

六.判断梯度下降是否收敛

七.如何设置学习率

八. 多项式回归

---

一.多维向量 

英文名：mutiple linear regression

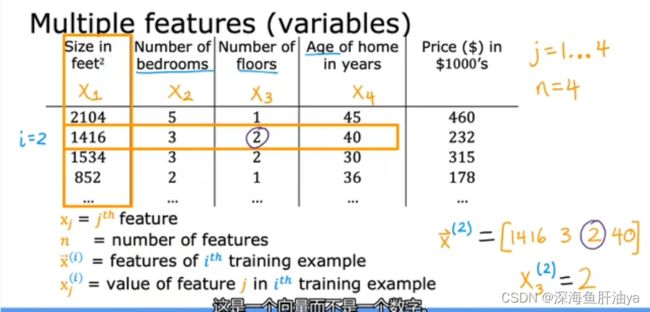
对于房价，我们可能不止面积大小一个因素影响价格，可能还有楼层数，卧室数量以及楼房的建造年纪等，所以这就引入了多个特征，我们通常把这多个特征写成一个向量，图中x的上标表示第几个训练示例，而下标代表当前训练示例中的第几个特征，结合起来就是第i个训练示例的第j个特征。n是特征的数量，下图中每行有4个特征，所以n=4。

有多个变量房价公式可能如下：

我们把上面那个式子用向量的方式来重新表示一下，把x也写成一个向量的形式，这样式子就可以简写为两个向量的点击加上一个常量。

 

二.向量化

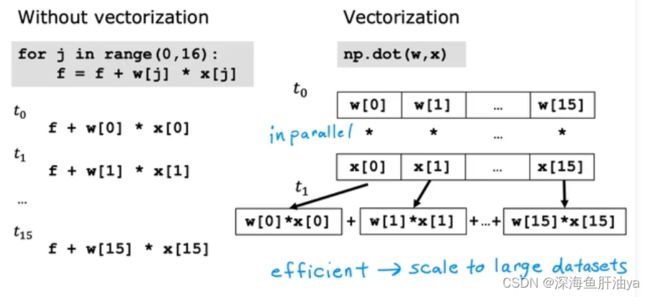
矢量化可以帮助我们的代码运行的更快。

红框处的代码用了numpy的函数，这比它左边的累加和上面的for循环都要更加快速

为什么矢量化之后运算会更快呢，原因就是numpy的这个函数做这个运算在电脑中相乘的部分是并行计算的，并且加起来的时候也很快，所以很快。同样的，加入现在你有很多特征，比如16个，那么如果再写一个for循环计算梯度，偏导等等，那会很慢，但是如果直接用numpy的函数的话，它会自动调用电脑的并行计算的硬件，可能16个还体会不到性能的差距，但是当n很大的时候，这个性能就体现出来了。

 

三.用于多元线性回归的梯度下降法

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：

 多元回归梯度下降的方法：

按照上式即可实现多元回归的梯度下降，注意式子的变化，最右边乘得是第i个训练示例的第j个特征（即一整个向量里的某个值），f里面是第i个训练示例（即一整个向量）。

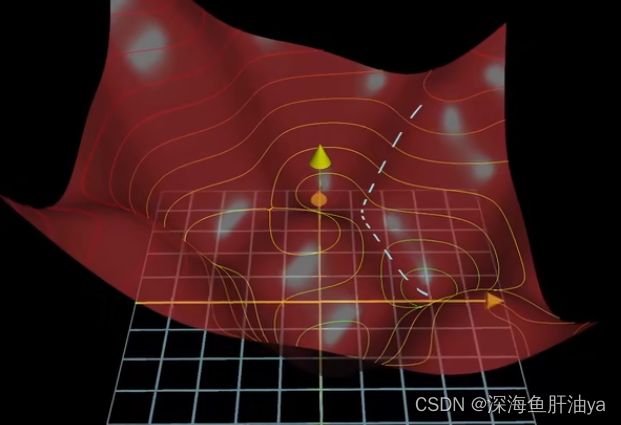
对于梯度下降的理解：

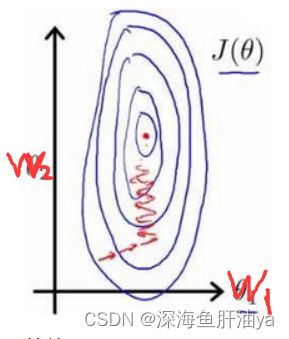
函数的梯度指出了函数的最陡增长方向，即是说按梯度的方向走函数值增长得就最快，那么沿梯度的负方向走函数值自然就降低得最快了，这个梯度向量的长度就代表了这个最陡的斜坡到底有多陡，你只要懂得让函数值最小的算法，其实不过是先计算梯度再按梯度反方向走一小步下山，然后循环。

四.正规方程

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。如：

正规方程无需迭代即可解决线性回归的问题，但是其也有一些缺点，就是这个方法没有推广到其他算法当中，如果特征数量很大，正规方程也很慢。只解决w和b的问题，所以用的比较少。

五.特征缩放

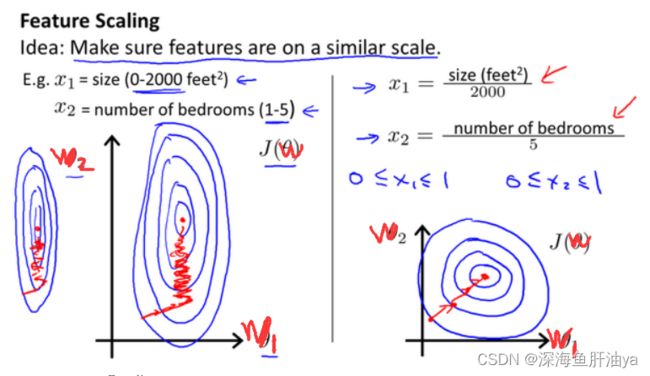
在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

再回顾一下等高线的图是如何绘制的，先把函数的三维图像画出来，然后从上往下切片，所以最外侧的圈就是成本最高的，最内侧的圈就是成本最低的（可以参考此系列文章的第一篇） 

解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间（其实是归一化）。如图：

下面是除最大值

下面是均值归一化 ：

这是以0为中心，最后缩放的范围通常是-1到1之间

就是一个值样本均值，然后再除样本的最大值与最小值的差值。

还有z-score标准化：

 分母那个符号是sigma（发音自行查阅），这里代表标准差；分子上的u1代表样本均值。

另外，我们在做特征缩放的时候，其实不用非得把它放到-1到1之间，看下面的图片，蓝色批注的都是可以的，而红色批注的都是不太好的，还是要尽量在-1到+1附近

 

注意，使用标准化特征进行预测，而使用原始特征值显示绘图。即如果我们得到的参数值（w，b）的过程当中把训练数据进行了特征缩放（即归一化），那么当我们预测的时候，我们也先去对预测的数据进行特征缩放（归一化）之后，再去预测。（看课后实验week2的3.的Lab03）

六.判断梯度下降是否收敛

当运行梯度下降时，如何判断它是否有效呢，及是否帮助你找到接近全局最小值的参数的成本函数。

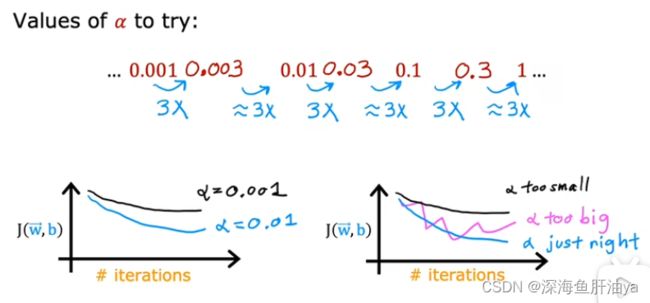
方法一就是查看学习曲线（咱们在第一周的代码里绘制过），如果梯度下降正常工作，那么每次迭代之后，成本应该是减小的，如果成本J在一次迭代之后增加，那么可能是学习率Alpha选择不当，这通常意味着Alpha太大或者代码中存在错误。

 方法二就是上图右侧，设置一个很小的数epsilon(高数里那个一步sei龙)，如果每次迭代减小的数小于这个epsilon的话，那么这个点之前的那些迭代你就可以声明收敛了，也即如果是在上图中的学习曲线里，这点左侧的曲线就是收敛的，但是一般设置一个合适的episilon是非常困难的。

七.如何设置学习率

 如果梯度下降不收敛，那儿我们通常做的一件事就是将学习率Alpha调小，

 通常可以考虑尝试些学习率：

Alpha=0.001，0.003，0.01，0.03，0.1，0.3，1

八. 多项式回归

 这种方法可以让你拟合曲线，非线性函数，下篇文章会详细讲这个，我们可以根据特征的合适选择以及多项式函数的合适选择来做拟合。

别忘了动手跑跑代码，老师课后的课件与代码能帮助我们查漏补缺，进入更深层次的理解。