Python之Pytorch--从入门到精通笔记

What is Pytorch？

Pytorch 是 torch 的 python 版本,是由 Facebook 开源的神经网络框架,专门针对 GPU 加速的深度神经网络 (DNN) 编程。简单说起来就是与 tensorflow 竞争的产品，不论使用哪一个，最终都能得到差不多的效果。

How to use Pytorch

了解一个框架（语言），最重要的环节便是熟悉语法、方法和接口。较为基础和重要的一些将列在下面。
首先默认你已经安装了 Pytorch 并且能够正常引入，并且已经学习并掌握了 numpy。

---

Numpy桥

同 tensorflow 一样，pytorch 的常用数据类型也是 Tensor，Tensor 是一种包含单一数据类型元素的多维矩阵，译作“张量”（张晟的弟弟）。
类比 numpy，一维 Tensor 叫 Vector，二维 Tensor叫 Matrix，三维及以上称为 Tensor。
而 numpy 和 Tensor 不仅仅有相似之处，还可以相互转换。

torch.from_numpy(ndarray) -> Tensor

import torch

# 声明一个 array，利用 from_numpy 将其转换为 tensor
np_data = np.array([7, 2, 3])
torch_data = torch.from_numpy(np_data)

此时得到的 torch_data 与 np_data 共享同一内存空间。修改其中一个另一个也会被修改，且返回的张量不能改变大小。

torch_data[0] = -1
print(np_data)

# 输出结果
# [-1, 2, 3]

同时 Tensor 也可以转换为 numpy.ndarray。

torch.numpy() -> ndarray

#将 torch_data 由 Tensor `转换为` numpy.ndarray ` 赋给 tensor2array
 tensor2array = torch_data.numpy()

---

Tensor 创建

对于 Python，常用的基本数据类型有 int、float、double 等，与之对应 Pytorch 也提供了多种类型的 tensor。

Pytorch 定了七种 CPU tensor 类型和八种 GPU tensor 类型：

数据类型	CPU Tensor	GPU Tensor
32-bit floating point	torch.FloatTensor	torch.cuda.FloatTensor
64-bit floating point	torch.DoubleTensor	torch.cuda.DoubleTensor
16-bit floating point	N/A	torch.cuda.HalfTensor
8-bit integer (unsigned)	torch.ByteTensor	torch.cuda.ByteTensor
8-bit integer (signed)	torch.CharTensor	torch.cuda.CharTensor
16-bit integer (signed)	torch.ShortTensor	torch.cuda.ShortTensor
32-bit integer (signed)	torch.IntTensor	torch.cuda.IntTensor
64-bit integer (signed)	torch.LongTensor	torch.cuda.LongTensor

torch.Tensor是默认的tensor类型（torch.FloatTensor）的简称。

# 构造一个 2*2 的张量
t1 = torch.Tensor(2,2)

# 等价于
# t1 = torch.FloatTensor(2,2)

# 同样地
# t2 = torch.IntTensor(2, 2)

一个张量还可以从 Python 的 list 或序列构建得到。

t1 = torch.FloatTensor([[1, 2, 3],
						[4, 5, 6]])

其次还有许多创建特殊矩阵的方法：

• torch.ones(n,m)： 创建n*m 维的张量，其元素都被填充了标量值1；
• torch.zeros(n,m)： 创建n*m 维的张量，其元素都被填充了标量值0；
• torch.eye(n,m)： 创建n*m 维的张量，其对角线为1，其余元素均为0；
• torch.linspace(start, end, steps=100) ： 创建值start和 end之间等间距点的一维张量；
• torch.rand(sizes)： 返回一个张量，包含了从区间[0,1)的均匀分布中抽取的一组随机数，其形状由整数序列sizes定义；
• torch.randn(sizes)： 返回一个张量，包含了从标准正态分布（均值为0，方差为1，即高斯白噪声）中抽取一组随机数，其形状由整数序列sizes定义。

在实际应用中，常常使用 torch.size() 获取 Tensor 的大小。

a = torch.randn(2,2)
print(a)
print(a.size())

# 输出结果
# 1.5346 -0.1640
# 0.7025  1.7613
# [torch.FloatTensor of size 2x2]

# torch.Size([2, 2])

---

Tensor 索引及切片

索引

1. 正序索引：Tensor 的索引值从 0 开始，范围从 0 到 size - 1。

t = torch.Tensor(range(5))
print(t)

# 索引为单个值
print(t[1])

# 索引为一个范围
print(t[0:3])

2. 逆序索引（tensor[ : , -1 ]）: 最后一个索引为 -1。
3. 负索引（tensor[ -3 ]）：表示倒数第三个元素，注意索引值的大小，始终是小值在冒号的前面，[ -3, -1 ]，大值在后。若写成[ -1, -3 ]将会报错。

切片
基本切片通过将 start, stop 和 step 参数提供给内置的 slice 函数来构造一个 Python slice 对象。此 slice 对象被传递给 Tensor 来提取 Tensor 的一部分。

t = torch.Tensor(range(5))
s = slice(2,5,2) 

print("Slicing Tensor : {}".format(t[s]))
print(t[2 : 5 : 2])

# 输出结果相同
# 2
# 4
# [torch.FloatTensor of size 2]

在二维情况下，以逗号进行分割。

tensor = torch.Tensor([[1, 2, 3],
					   [4, 5, 6],
					   [7, 8, 9],
					   [10, 11, 12]])
print(tensor[0 : 3 : 2, : ])

# 输出结果
# 1 2 3
# 7 8 9

还有其他常用函数：
torch.chunk(tensor, chunks, dim = 0)
将张量沿给定维度拆分成若干块。（将要拆分的张量，返回的块数，所沿拆分维度）

torch.cat(seq, dim = 0, out = None) -> Tensor
在给定维度上连接张量的给定序列。（Python 序列，张量连接的维度，输出参数）

torch.unsqueeze(input, dim, out = None)
返回在指定位置插入尺寸为1的新张量。（输入的张量，插入单个维度的索引，结果张量）

---

基本运算

相加

1. x + y
2. torch.add(x, y)
3. y.add_(x)

x = torch.Tensor(2, 3)
y = torch.rand(2, 3)

print(x + y)
print(torch.add(x, y))

y.add_(x)
print(y)

# 输出结果相同
# 函数后带下划线表示是否改变原 tensor 值
# y.add_(x) 会在原地求和，并返回改变后的 tensor，
# 而 y.add(x)将会在一个新的 tensor 中计算结果， y 本身不改变。

类似的

函数	描述
torch.sqrt(t)	返回一个新张量，元素为输入的元素开方后的结果
torch.round(t)	返回一个新张量，元素为输入的元素四舍五入到最接近的整数
torch.sign(t)	返回一个新张量，元素为输入的元素的符号，正为1，负为-1
torch.transpose(t)	返回一个新张量，为原来张量的转置
torch.abs(t)	返回一个新张量，元素为输入元素的绝对值
torch.ceil(t)	返回一个新张量，元素为大于输入元素最小的整数
torch.cos(t)	返回一个新张量，元素为输入元素的 cos值
torch.sin(t)	返回一个新张量，元素为输入元素的sin值

---

Reshape

view
在处理数据时，由于不同的需求，我们常常需要将数据进行扩充或者在尺寸上进行变化以进行操作。

这里我们使用 view() 方法，返回具有相同数据但大小不同的新张量，从而达到了 reshape 的作用。

view(args) -> Tensor
返回具有相同数据但大小不同的张量。张量必须 contiguous() 才能被查看。
关于 contiguous()，可以参考下面这篇博客，讲的很不错！

https://blog.csdn.net/kdongyi/article/details/108180250

转置
由下面两种转置产生的结果张量，与输入张量共享存储。

torch.t(input, out = None) -> Tensor
将输入的二维张量转置其维度 0 和 1。（只适用于二维张量）

x = torch.randn(5, 10)
print(x.t().size())

# 输出结果
# torch.Size([10, 5])

torch.transpose(input, dim0, dim1, out = None) -> Tensor
返回一个输入转置后的张量，使两个维度相互交换。

y = torch.randn(5, 10, 15)
print(y.transpose(0, 1).size())
print(y.transpose(1, 2).size())

# 输出结果
# torch.Size([10, 5, 15])
# torch.Size([5, 15, 10])

---

求导及梯度

在 0.4 版本以前，pytorch 使用 Variable 进行自动求导和梯度，可以参考这篇文章：

https://zhuanlan.zhihu.com/p/104519573

现在推荐使用的方法如下：
在 Tensor 中有一个参数 requires_grad，表示是否可以求导，即求梯度，默认值为 False。需要注意的是，当叶子结点有一个为可导，则根结点可导。

在使用中，我们通过：
x.requires_grad_(True / False)
设置 tensor 可导与否。但是我们只能这样设置叶子变量，否则会报错！

我们针对一个函数求梯度：

x为 2 * 2 的值全为1的张量
$y_i=(x_i+4{)}^2$
$z_i=y_i^2+x_i+2$
$out=\frac{1}{4}{\sum }_{i=1}^4{z}_i$

下面对 out 求关于 x 的导数：

$\frac{\partial out}{\partial x}=(x+4{)}^3+0.25=125.25$

然后编程验证：

x = torch.ones(2, 2, requires_grad = True)
y = (x + 4) ** 2
z = y**2 + x + 2
out = z.mean()
out.backward()
print(x.grad)

# 输出结果
# tensor([[125.2500, 125.2500],
#         [125.2500, 125.2500]])

我们可以使用 with torch.no_grad() 来停止梯度的计算：

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
	print((x ** 2).requires_grad)

# 输出结果
# True
# True
# False

---

神经网络

友情提示：从这里开始需要具备深度学习神经网络相关知识。

torch.nn.Module

我们使用 torch.nn 来构建神经网络。

• 线性图层： nn.Linear，nn.Bilinear
• 卷积层： nn.Conv1d，nn.Conv2d，nn.Conv3d，nn.ConvTranspose2d
• 非线性： nn.Sigmoid，nn.Tanh，nn.ReLU，nn.LeakyReLU
• 池化层： nn.MaxPool1d，nn.AveragePool2d
• Recurrent网络： nn.LSTM，nn.GRU
• 标准化： nn.BatchNorm2d
• Dropout： nn.Dropout，nn.Dropout2d
• Embedding： nn.Embedding
• 损失函数： nn.MSELoss，nn.CrossEntropyLoss，nn.NLLLoss

这些类的实例具有一个内置的__call__函数，可以通过图层运行输入。

import torch.nn as nn
import torch.nn.functional as F

class My_Model(nn.Module):
    def __init__(self):
        super(My_Model, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5)
        self.conv2 = nn.Conv2d(20, 20, 5)
        
    def forward(self, x):
       x = F.relu(self.conv1(x))
       return F.relu(self.conv2(x))

l = nn.Linear(2, 2)
net = nn.Sequential(l, l)

print(l)
print(net)
for idx, m in enumerate(net.modules()):
	print(idx, '->', m)

# 输出结果
# Linear(in_features=2, out_features=2)
# Sequential(
#  (0): Linear(in_features=2, out_features=2)
#  (1): Linear(in_features=2, out_features=2)
#)
# 0 -> Sequential(
#  (0): Linear(in_features=2, out_features=2)
#  (1): Linear(in_features=2, out_features=2)
# )
# 1 -> Linear(in_features=2, out_features=2)

torch.nn.Sequential 是一个序列化的模块，将按照它们在构造函数中传递的顺序添加到其中，或者可以传入模块的有序字典。

---

torch.nn.Linear

我们使用
torch.nn.Linear(in_data, out_data, bias = True)
来对输入数据应用一个线性转换：$y=Ax+b$

参数说明：

• in_data：输入样本大小
• out_data：输出样本大小
• bias：偏移量，是否学习额外的偏移量，默认为 True

module = nn.Linear(4, 2)
print(module)

# Linear(in_features=4, out_features=2)

注意
如果不理解线性转换，可以思考输入输出都是一维的情况：

linear = nn.Linear(1, 1)
tens = Variable(torch.Tensor([1]))
out = linear(tens)

print('权重为：', end = '')
print(linear.weight)
print('偏差为：', end = '')
print(linear.bias)
print('数据为：', end = '')
print(tens[0])
print('输出结果：', end = '')
print(out)

# 输出结果
# 权重为：Parameter containing:
# tensor([[-0.1829]], requires_grad=True)
# 偏差为：Parameter containing:
# tensor([-0.7048], requires_grad=True)
# 数据为：tensor(1.)
# 输出结果：tensor([-0.8877], grad_fn=)

# 即 -0.1829 * 1 + （-0.7048） = -0.8877
# k * x + b 

下面观察二维情况

linear = nn.Linear(2, 2)
tens = Variable(torch.Tensor([[2, 2], [1, 1]]))
out = linear(tens)

print('权重为：', end = '')
print(linear.weight)
print('偏差为：', end = '')
print(linear.bias)
print('数据为：', end = '')
print(tens)
print('输出结果：', end = '')
print(out)

# 输出结果

# 权重为：Parameter containing:
# tensor([[ 0.5728, -0.3790],
#         [-0.4077, -0.5106]], requires_grad=True)

# 偏差为：Parameter containing:
# tensor([-0.2271, -0.0608], requires_grad=True)

# 数据为：tensor([[2., 2.],
#                [1., 1.]])

# 输出结果：tensor([[ 0.1607, -1.8974],
#                  [-0.0332, -0.9791]], grad_fn=)

不难发现，我们以为的线性运算过程是：

$$\left[\begin{array}{cc}0.5728& -0.3790\\ -0.4077& -0.5106\end{array}\right]\ast \left[\begin{array}{cc}2& 2\\ 1& 1\end{array}\right]+\left[\begin{array}{cc}-0.2271& -0.0608\\ -0.2271& -0.0608\end{array}\right]=\left[\begin{array}{cc}0.5395& 0.7058\\ -1.5531& -1.3868\end{array}\right]$$

很明显结果不正确，于是我们查看源码：

正确的计算过程是：已知矩阵叉乘权重矩阵的转置，再加偏差。

$$\left[\begin{array}{cc}2& 2\\ 1& 1\end{array}\right]\ast {\left[\begin{array}{cc}0.5728& -0.3790\\ -0.4077& -0.5106\end{array}\right]}^T+\left[\begin{array}{cc}-0.2271& -0.0608\\ -0.2271& -0.0608\end{array}\right]=\left[\begin{array}{cc}0.1607& -1.8974\\ -0.0332& -0.9791\end{array}\right]$$

---

非线性模型

在实际应用中，非线性模型往往更加好用，比如我们熟悉的（假装你熟悉） ReLU、Threshold、Sigmoid、Tanh。下面我们逐个来看。
1. ReLU

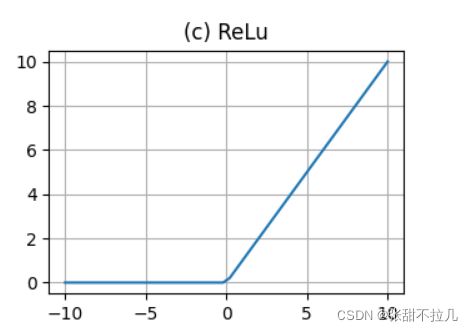
m = nn.ReLU()
input = Variable(torch.randn(2))
print(input)
print(m(input))

# 输出结果
# -0.1006	小于零
# 2.0656	大于零

# 0.0000
# 2.0656

2.Threshold
将输入张量每个元素二值化。

m = nn.Threshold(0.1, 20)
input = Variable(torch.randn(2))
print(input)
print(m(input))

# 输出结果
# -0.923	# 小于0.1
# 1.1429

# 20.000
# 1.1429

3. Sigmoid
公式：
$f(x)=\frac{1}{e^{-x}+1}$
图像：

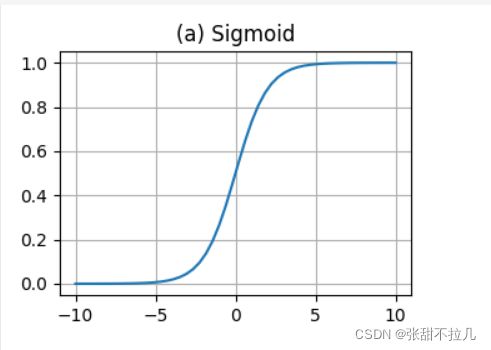
Sigmoid 是我们在进行神经网络训练中经常会看到的一个函数，也叫 Logistic 函数，他可以将一个实数映射到（0，1）的区间，可以用来做二分类。在特征相差比较复杂或是相差不大时效果特别好。

m = nn.Sigmoid()
input = Variable(torch(randn(2))
print(input)
print(m(input))

# 输出结果
# -1.2118
# -0.6524

# 0.2294
# 0.3424

4.Tanh()
双曲正切函数公式：
$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
图像：

tanh 在特征相差明显时效果会很好，在循环过程中会不断扩大特征效果。与 sigmoid 相比，tanh 是0均值的，因此在实际应用中 tanh 比 sigmoid 更好。
不难看出，二者有以下关系：
$tanh(x)=2sigmoid(2x)-1$

m = nn.Tanh()
input = Variable(torch.Tensor([2.3, -1.4]))
print(input)
print(m(input))

# 输出结果
# 2.3
# -1.4

# 0.9801
# -0.8854

---

卷积

终于到了神经网络的关键环节~卷积！
卷积本质就是用卷积核的参数来提取原始数据的特征，通过矩阵点乘运算，提取出和卷积核特征一致的值，这里提示可以不用从特征的角度理解卷积，因为实际上卷积得到的是一些加权求和的浓缩结果。这里对于卷积操作过程不再赘述。
conv1d
一维卷积

torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride = 1, padding = 0, dilation = 1, groups = 1, bias = True)

参数说明：
in_channels： 输入图像中的通道数量
out_channels： 卷积产生的通道数
stride： 循环内核的大小
padding： 滑动窗口，指每次卷积对原数据滑动 n 个单元格
dilation： 是否填充0
groups： 将数据分组，通常默认即可
bias： 偏移量参数，通常默认即可

m = nn.Conv1d(16, 33, 3, stride = 2)
input = Variable(torch.randn(20, 16, 50))
output = m(input)
print(output.size())

# 输出结果
# torch.Size([20, 33, 24])

conv2d
与1维差不多，计算宽高。

m = nn.Conv2d(16, 33, 3, stride = 2)
k = nn.COnv2d(16, 33, (3, 5), stride = (2, 1), padding = (4, 2))

input = Variable(torch.randn(20, 16, 50, 100))
output1 = m(input)
output2 = m(input)
print(output1.size())
print(output2.size())

---

池化

在神经网络中，池化层往往跟在卷积层后面，通过平均池化或者最大池化的方法将之前卷积层得到的特征图进行一个聚合统计，从而达到压缩数据量的目的。

在 Pytorch 中池化分为平均池化 AvgPool 和最大池化 MaxPool 两种。两者的区别在于 MaxPool 需要记录下池化操作时哪个像素的值是最大，也就是 max id，这个变量在反向传播中要用到。
AvgPool1d、AvgPool2d、AvgPool3d

torch.nn.AvgPool1d(kernel_size, stride = None, padding = 0, ceil_mode = False, count_include_pad = True)

m = nn.AvgPool1d(3, stride = 2)
output = m(Variable(torch.Tensor([[[1, 2, 3, 4, 5, 6, 7]]]))
print(output)

# 输出结果
# 2 4 6

MaxPool 用法类似。

---

正则化

正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。
在 Pytorch 中，我们使用 BatchNorm 来进行正则化操作。
PyTorch 提供了四种常用的 Norm 层，包括 BatchNorm、LayerNorm、InstanceNorm 和 GroupNorm。

1. BatchNorm

torch.nn.BatchNorm1d(num_features, eps = 1e-05, momentum = 0.1, affine = True)

参数说明：
num_features： 由输入的 batch_sizenum_featureswidth 计算得出
eps： 为数值稳定性添加分母的值，默认为 1e-5
momentum： 用于 running_mean 和 running_var 计算的值
affine： 当设置为 True 时，给出图层可学习的仿射参数

input = Variable(torch.Tensor([[1, 2, 3], [2, 3, 4]]))

m = nn.BatchNorm1d(3)
output = m(input)
print(output)

m1 = nn.BatchNorm1d(3, affine = False)
output1 = m1(input)
print(output1)

# m 可以调用 weight 和 bias 进行赋值
m.weight = nn.Parameter([torch.Tensor([1, 1, 1]))

# 输出结果
# Variable containing:
# -0.3008 -0.7367 -0.3441
#  0.3008  0.7367  0.3441
# [torch.FloatTensor of size 2x3]
# Variable containing:
# -1.0000 -1.0000 -1.0000
# 1.0000  1.0000  1.0000
# [torch.FloatTensor of size 2x3]

2. InstanceNorm
关于各种 Norm 的理解，推荐下面一篇文章，这里只做使用概述。

https://blog.csdn.net/longrootchen/article/details/105650059

input = Variable(torch.randn(1, 5, 2))
# Without Learnable Parameters
m = nn.InstanceNorm1d(5)
output = m(input)
print(output)
# With Learnable Parameters
m1 = nn.InstanceNorm1d(5, affine=True)
output1 = m1(input)
print(output1)

---

损失函数

损失函数用来评价模型的预测值和真实值差距的程度，深度学习训练模型的时候就是通过计算损失函数，更新模型参数，从而减小优化误差，直到损失函数值下降到目标值或者达到了训练次数。
1. L1Loss

torch.nn.L1Loss(size_average = True, reduce = True)

$loss(x,y)=\frac{sum|x_i-y_i|}{n}$

参数说明：
size_average： 默认情况下对每个 mini-batch 的损失取平均值，设置为 False 时每个 mini-batch 损失将被相加。当 reduce 为 False 时忽略该参数。
reduce： 默认情况下，损失是每个 mini-batch 的平均或总和，设置为 False 时，损失函数会返回每个 batch 元素的损失，而忽略 size_average。

loss = nn.L1Loss()
input1 = Variable(torch.randn(3, 5), requires_grad=True)
target = Variable(torch.randn(3, 5))
output = loss(input1, target)
print(output)

2. MSELoss

torch.nn.MSELoss(size_average = True, reduce = True)

$loss(x,y)=\frac{sum|x_i-y_i{|}^2}{n}$

loss = nn.MSELoss()
input1 = Variable(torch.randn(3, 5), requires_grad=True)
target = Variable(torch.randn(3, 5))
output = loss(input1, target)
print(output)

3. CrossEntropyLoss
著名的交叉熵，来自香农的信息论，简单来说，交叉熵是用来衡量在给定的真实分布 pk 下，使用非真实分布 qk 所指定的策略 f(x) 消除系统的不确定性所需要付出的努力大小。
交叉熵越小，就证明算法所产生的策略越接近最优策略，即非真实分布接近真实分布。

torch.nn.CrossEntropyLoss(weight = None, size_average = True, ignore_index = -100, reduce = True)

$loss(x,class)=-log\frac{exp(x[class])}{su{m}_{j}exp(x[j])}=-x[class]+log(su{m}_{j}exp(x[j]))$

参数说明：
weight： 给每个类手动缩放权重，如果给出，则必须是维度为类别总数的张量
size_average： 与上同
ignore_index： 指定被忽略的目标值，不影响输入梯度，当值为 True 时，损失是对未被忽略的目标进行平均
reduce： 与上同

Pytorch 中 CrossEntropyLoss 是通过两个步骤计算出来的，第一步是计算 log softmax，第二步是计算 cross entropy，CrossEntropyLoss 不需要在网络的最后一层添加 softmax 和 log 层，直接输出全连接层即可。

# 预测值f(x) 构造样本，神经网络输出层
inputs_tensor = torch.FloatTensor( [
 [10, 2, 1,-2,-3],
 [-1,-6,-0,-3,-5],
 [-5, 4, 8, 2, 1]
 ])
# 真值y
targets_tensor = torch.LongTensor([1,3,2])
# targets_tensor = torch.LongTensor([1])

input1 = Variable(inputs_tensor, requires_grad=True) 
target = Variable(targets_tensor)
loss = nn.CrossEntropyLoss()
output = loss(input1, target)
print(output)

# 输出结果
# Variable containing:
#  3.7925
# [torch.FloatTensor of size 1]

---

距离函数

做分类任务时常常需要估算不同样本之间的相似性度量，这是通常采用的方法就是计算样本间的“距离”。
CosineSimilarity

torch.nn.CosineSimilarity(dim = 1, eps = 1e-08)

$similarity=\frac{x_1\cdot x_2}{max(||x_1|{|}_2\cdot ||x_2|{|}_2,ϵ)}$

参数说明：
dim： 计算余弦相似度的维度，默认为1
eps： 小值以避免被0除，默认1e-8

input1 = Variable(torch.randn(5, 12))
input2 = Variable(torch.randn(5, 12))

cos = nn.CosineSimilarity(dim=1, eps=1e-6)

output = cos(input1, input2)
print(output)

PairwiseDistance

torch.nn.PairwiseDistance(p = 2, eps = 1e-06)

$||x_1|{|}_p:=({\Sigma }^{1\le i\le n}|x_i{|}^p{)}^p$

参数说明：
p： 范数，默认为2
eps： 小值以避免被0除

pdist = nn.PairwiseDistance(p=2)
output = pdist(input1, input2)
print(output)

---

优化

在损失定义的情况下，最小化处理任务交给优化器处理，使用 torch.optim，构造一个 optimizer 对象，用来保存当前的参数状态且基于计算梯度更新参数。

# 引入优化算法库
import torch.optim
import torch
from torch.autograd import Variable
import torch.nn as nn

下面举出三种优化器的例子。

# SGD 优化，网络为 model
optimizer = optim.SGD(model.parameters(), lr = 0.01, weight_decay = 0)

# Adam 优化
optimizer = optim.Adam([var1, var2], lr = 0.0001)

单次优化
所有的 optimizer 都实现了 step() 方法，这个方法更新所有参数。
一旦梯度被如 backward() 之类的函数计算好，我们就可以调用 optimizer.step() 来进行优化。

使用示例：

for input, target in dataset:
	# 每次迭代清空上一次的梯度
	optimizer.zero_grad()
	# 使用模型
	output = model(input)
	# 计算损失
	loss = loss_fn(output, target)
	# 反向传播
	loss.backward()
	# 更新梯度
	optimizer.step()

某些优化器需要进行重复多次计算，需要传入一个闭包才允许进行重新计算。

查看优化器参数

print(optimizer.param_groups)
print(optimizer.param_groups[0]['lr'])

# 输出结果过长自行测试

---

本文参考：

1. https://blog.csdn.net/qq_48314528/article/details/121604848
2. https://www.educoder.net/paths/sqf4o7bj