密码学---流密码
流密码
- 流密码
-
- 基本思想
- 设计原则
- 基本概念
-
- 一次一密密码
- 同步流密码
- 有限状态自动机
- 线性反馈移位寄存器
-
- 线性反馈移位寄存器的一元多项式表示
-
- 定义
- 定理
- m序列
-
- 基本概念
- m序列的伪随机性
-
- 伪随机序列
- 需要满足条件
- 定理
- m序列密码的破译
-
- 破译示例
- 同步流密码加密器的组成
-
- 组成1---密钥流产生器
-
- 密钥流产生器的组成
- 密钥流产生器的设计关键
- 组成2---加密变换器
- 密钥流产生器
-
- 驱动部分--线性反馈移位寄存器
-
- 线性反馈移位寄存器的例子
- 线性反馈移位寄存器的注意事项
- 非线性组合部分
-
- 1.Geffe序列生成器
-
- 组成
- 流程
- 周期
- 线性复杂度
- 2.JK触发器
-
- 组成
- 流程
- 周期
- JK真值表
- 3.Pless生成器
- 4.时钟序列生成器
-
- 组成
- 流程
- 周期
- 线性复杂度
- 实际例子
流密码是按单个字符组个进行加密的密码学。
流密码
基本思想
流密码的基本思想是利用密钥k产生一个密钥流z=z0z1z2…,并使用如下加密规则对明文串x=x0x1x2…加密,得到加密后的密文y=y0y1y2…=Ez0(x0)Ez1(x1)…。
其中密钥流由密钥流发生器f产生,i时刻的滚动密钥zi由i时刻的记忆元件(存储器)的状态σi和密钥k共同决定。需要注意的是,由于输入的明文可能会影响记忆元件(存储器)的状态σi,因此σi可能依赖于密钥k,初始状态σ0,x0,x1,x2,…,xi-1等参数
![]()
分组密码和流密码的区别就在于是否有记忆性。
设计原则
使密钥流生成器要有不可预测性,具体表现如下:
- 长周期
- 高线性复杂度
- 统计性能良好
- 足够的“混乱”
- 足够的“扩散”
- 抵抗不同形式的攻击
基本概念
根据加密器中记忆元件的存储状态σi是否依赖于输入的明文字符,可将流密码进一步分成同步和自同步两种。其中同步流密码的σi独立于明文字符,自同步流密码的σi与明文字符有关,因此较难从理论上对自同步流密码进行分析。
一次一密密码
一次一密密码是一种理想的加密方法,即每次加密都使用一次一密乱码本来进行移位取模运行,从而得到加密后的密文。其中一次一密乱码本是一个由固定字符集随机组成的一串与明文长度相等的字符,且每次加密过程都会使用不同的一次一密乱码本来进行加密操作,因此被称为一次一密密码。
同步流密码
因为同步流密码的滚动密钥zi与明文字符无关,因此密文字符yi也与明文字符无关,因此可将同步流密码的加密器分成密钥流产生器和加密变换器两部分。同步流密码的体制模型如下:
有限状态自动机
有限自动状态机是具有离散输入和输出(输入集和输出集有限)的一种数学模型。由以下三部分组成:
1.有限状态集S={si|i=1,2,3,…,l}
2.有限输入字符集A1={Aj(1)|j=1,2,…,m}和有限输出字符集A2={Ak(2)|k=1,2,…,n}
3.转移函数如下:
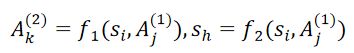
即在状态为si,输入为Aj(1)时,输出为Ak(2),而此时的状态转移为sh。
有限状态自动机可用有向图表示,也称为转移图。转移图的顶点对应于自动机的状态,弧线(Ai(1),Aj(2))表示在状态si在输入Ai(1)时转为状态sj,且输出一个字符Aj(2),所以弧线(Ai(1),Aj(2))从状态si转移到sj。
线性反馈移位寄存器
移位寄存器是密钥流生成器的一个主要部分,GF(2)上一个n级反馈寄存器是由n个二元存储器和一个反馈函数f(a1,a2,a3,…,an)组成。其中ai表示第i级存储器的内容,可取0和1两个值,反馈函数是用来确定下一个时刻的状态的。
实际应用中,密钥流生成器常采用线性的驱动部分,因此我们这里主要讨论线性反馈移位寄存器(LFSR)。线性反馈移位寄存器是指反馈函数f(a1,a2,a3,…,an)是关于a1,a2,a3,…,an的线性函数的移位寄存器。因此f可以表示为:
![]()
线性移位寄存器实现简单、速度快、有较为成熟的理论基础因此成为构造密钥流生成器的重要部分之一。
线性反馈移位寄存器的一元多项式表示
设n级线性反馈移位寄存器的输出序列{ai}满足递推关系如下关系:
![]()
对任何k≥1成立。则这种递推关系可用一个一元高次多项式表示:
![]()
则称这个多项式为LFSR的特征多项式。
定义
LFSR多项式表示的阶或周期:设p(x)是GF(2)上的多项式,使P(x)|(xp-1)的最小p称为p(x)的周期或者阶。其中|是整除符号,即a|b,a是b的因数
不可约多项式或即约多项式:仅能被非0常数或自身的常数倍除尽,但不能被其他多项式除尽的多项式称为不可约多项式或即约多项式
n次本原多项式:若n次不可约多项式的P(x)的阶为2n-1,则称p(x)是n次本原多项式
定理
设p(x)=1+c1x+…+cnxn是GF(2)上的多项式,G(P(x))中任一序列{ai}的生成函数A(x)满足如下关系式:
p(x)|q(x)的充要条件是G(p(x))⊂G(q(x))
若序列{ai}的特征多项式p(x)定义在GF(2)上,p是p(x)的周期,则{ai}的周期r|q
设p(x)是n次不可约多项式,周期为m,序列{ai}∈G(p(x)),则{ai}的周期为m
n级LFSR产生的序列有最大周期2n-1的必要条件是其特征多项式为不可约的
设{ai}∈G(p(x)),{ai}为m序列的充要条件是p(x)为本原多项式,且对于任意的正整数n,至少存在一个n次本原多项式。
m序列
m序列是指周期达到最大值的序列。若是n级线性反馈移位寄存器,则当其状态周期达到2n-1,即输出序列的周期为2n-1,则该输出序列为m序列。
基本概念
异相自相关函数:GF(2)上周期为T的序列{ai}的自相关函数定义如下:
其中求和表示的是序列{ai}和{ai+τ}(序列{ai}向后平移T位得到)在一个周期内对应位相同的位数与对应位不同的位数之差。当T=0时,R(T)=1;当T≠0时,称R(T)为异相自相关函数。
m序列的伪随机性
流密码的安全性取决于密钥流的安全性,要求密钥流序列有好的随机性,从而使密码分析者无法对密钥流进行预测。
由于密钥流是周期的,要完全做到随机性是很困难的。因此这里就提出了伪随机性。
伪随机序列
只要截获比周期短的一段密文时内不会泄露更多信息,这样的序列称为伪随机序列。
需要满足条件
Golomb对伪随机序列提出了应满足的如下3个随机性公设:
1.在序列的一个周期内,0与1的个数相差至多为1
2.在序列的一个周期内,长为1的游程占游程总数的1/2,长为2的游程占游程总数的1/22,长为i的游程占游程总数的1/2i,且在等长的游程中0的游程个数和1的游程个数相等
3.异自相关函数是一个常数
除此之外,还应该满足下面的条件:
1.{ai}的周期相当大
2.{ai}的确定在计算上是非常容易的
3.由密文及相应的明文的部分信息,不能确定整个{ai}
定理
GF(2)上的n长m序列{ai}具有如下性质:
1.在一个周期内,0、1出现的次数分别为2n-1-1和2n-1
2.在一个周期内,总游程数为2n-1;对1≤i≤n-2,长为i的游程有2n-i-1个,且0、1游程各半;长为n-1的0游程一个,长为n的1游程一个;
3.{ai}的自相关函数为如下:

m序列密码的破译
前提条件:滚动密钥生成器是线性反馈移位寄存器,产生的密钥是m序列。
设Sh和Sh+1是序列中两个连续的n长向量,其中:

设序列的递推关系:ak+n=c1ak+n-1⊕c2ak+n-2⊕c3ak+n-3…⊕cnak
也可表示为如下关系:

破译过程如下:
前提条件:已知一段长为2n的明密文对,即已知x=x1x2x3…x2n,y=y1y2y3…y2n
步骤:
- 得到LFSR的连续n+1个状态(S1=(z1z2z3…zn),S2=(z2z3z4…zn+1),…,Sn=(znzn+1zn+2…z2n-1),Sn+1=(zn+1zn+2zn+3…z2n)),可以记zi为ai
- 有如下关系成立:

- 由于X可逆,对2中的等式变形:

破译示例
同步流密码加密器的组成
组成1—密钥流产生器
密钥流产生器是同步流密码的关键。而在实际应用中,密码设计者常希望设计出一个滚动密钥生成器,使得密钥k经其扩展成的密钥流序列z具有极大的周期,良好的统计特性,抗线性分析,抗统计分析。
密钥流产生器的组成
密钥流产生器的设计关键
找出适当的状态转移函数φ和输出函数ψ,使得输出序列z满足密钥流序列z应满足的随机性条件,并且要求在设备上是节省的和容易实现的。
一般采用线性的φ和非线性的ψ,这样能够得到好的生成器。可将这样的密钥流产生器分成驱动部分(常由一个或多个线性反馈移位寄存器实现)和非线性组合部分(常用非线性组合函数F实现)。其中驱动部分控制生成器的状态转移,并为非线性组合部分提供统计行能好的序列,而非线性部分要利用这些序列组合出满足要求的密钥流序列。密钥流生成器的结构吐下:

组成2—加密变换器
加密变换Ezi可以有多种选择,只要保证加密变换是可逆的即可。但是常采用非线性函数来进行加密变换,这样能够得到更好的密钥流生成器。
密钥流产生器
前面说过,密钥流产生器可看成是由一个驱动部分和一个非线性组合部分构成。其中驱动部分常由一个或多个线性反馈移位寄存器组成,而非线性组合部分常用非线性组合函数F来实现。
为了使密钥流生成器输出的二元序列尽可能复杂,应保证其周期尽可能大、线性复杂度和不可预测性尽可能高,因此常使用多个LFSR来构造二元序列,称每个LFSR的输出序列为驱动序列,显然密钥流生成器输出序列的周期不大于各驱动序列周期的乘积,因此,提高输出序列的线性复杂度应从极大化其周期开始。
二元序列的线性复杂度指生成该序列的最短LFSR的级数,最短LFSR的特征多项式称为二元序列的极小特征多项式。
驱动部分–线性反馈移位寄存器
目前最为流行和实用的密钥流产生器的驱动部分常常是一个或多个线性反馈移位寄存器,如图所示:

线性反馈移位寄存器的例子
如图所示,是一个5级线性反馈移位寄存器:

其反馈函数可以表示为f(a1,a2,a3,a4,a5)=a4⊕a1
⊕是异或运算法,1⊕1=0,1⊕0=1,0⊕1=1,0⊕0=0
线性反馈移位寄存器的注意事项
- n级线性反馈移位寄存器最多有2n个不同的状态
- 若初始状态全为0,则后面的状态均为0
- n级线性反馈移位寄存器的状态周期小于等于2n-1
- 输出序列的周期与状态周期相等
非线性组合部分
下面介绍一些由多个LFSR驱动的非线性序列生成器
1.Geffe序列生成器
组成
由3个LFSR组成,其中LFSR2作为控制生成器使用,结构如图所示:

流程
当LFSR2的输出为0时,表示LFSR1和LFSR3相连接;当LFSR2的输出为1时,表示LFSR1和LFSR2相连接。
可设LFSRi的输出序列为{ak(i) }(i=1,2,3),则Geffe序列生成器的输出序列{bk}可表示为bk=ak1ak(2)+ak(3)(1-ak(2))
周期
由于LFSRi的特征多项式分别为ni次本原多项式,且ni两两互素,则Geffe序列的周期T为:

线性复杂度
![]()
Geffe序列生成器的另一种表示方式:将LFSR1和LFSR3看成是多路复合器的输入,LFSR2看成是多路复合器的输出。其结构图如下:

2.JK触发器
组成
由两个输入端J、K和一个前输出位ck-1组成,其结构图如下所示:

利用JK触发器的非线性序列生成器结构如图所示:其中{ak}是m级m序列,{bk}是n级m序列

流程
基于JK触发器的非线性序列生成器的输出序列表示:
![]()
且由表达式,可以推出:

周期
当m和n互素且a0+b0=1时,周期为(2m-1)(2n-1)
复杂度:知道{ck}中相邻位的值ck-1和ck,就可以推断出ak和bk中的一个
JK真值表
3.Pless生成器
在JK触发器的基础上进行改进,由多个JK触发器和循环计数器构成,循环计数器的作用是进行选通控制。结构如图所示:
4.时钟序列生成器
组成
由一个LFSR控制另外一个LFSR的移位时钟脉冲,结构如图所示:

流程
前提条件:假设LFSR1和LFSR2的输出序列分别为{ai}和{bi},其周期分别为p1和p2。
过程:当LFSR1输出为1时,移位时钟脉冲通过与门使LFSR2进行一次移位,从而生成下一位;当LFSR1输出为0时,移位时钟脉冲无法通过与门影响LFSR2,因此LFSR2重复输出前一位。
周期
假设钟控序列{ck}的周期为p,可得如下周期关系:

因为p1=2m-1,p2=2n-1。又w1=2m-1,所以gcd(w1,p2)=1,因此p=p1p2=(2m-1)(2n-1)
线性复杂度
线性复杂度为n(2m-1)







