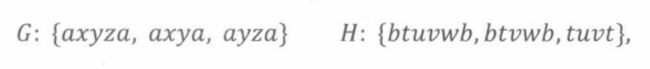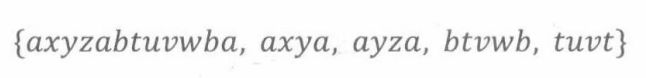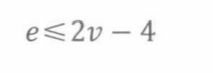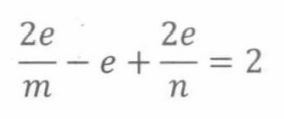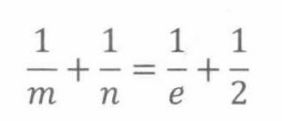第13章 平面图

第13章 平面图

13.1 在平面上绘制图形

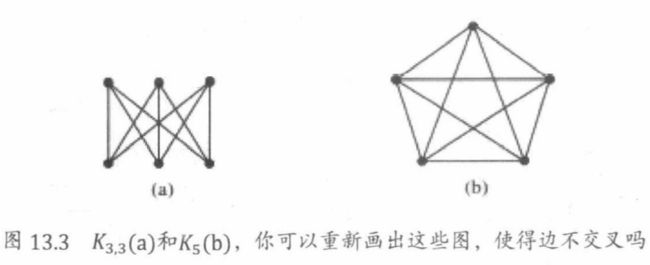
对于如下两个图形，你能否找到一种方式去重画这些边，使得这些边不交叉。

a图形：它有6个节点开且前3个节点与后3个节点之间可以形成边。这种图被称为完全二分图$k_{3,3}$。
b图形：有五个点，每一个点都与其他四个点有一条连线。

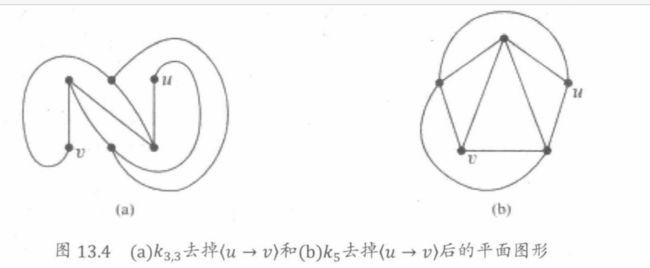
对于以上每种情形，答案都是“没有,但几乎有!”。只要移去一条边，那么这些图就可以画在平面上。

平面图形已经应用于电路设计中，对于显示图形数据，如程序流程图、组织结构图和行程安排冲突也很有帮助。在这些应用中，我们的目标是在平面上绘图时尽可能地避免边与边之间的交叉。

13.2 平面图的定义

定义13.2.1：在平面上绘制一幅图，就是将每个节点指定为一个独特的点，将每条边指定为一条平滑的曲线。其端点对应于与这条边相连的节点。如果没有曲线与自己或其他曲线交叉，则图形是平面的。换句话说，在任何曲线上出现不止一次的点，必须是节点。当图有平面图形时，它就是平面的。

定义13.2.1中使用了平面图形来定义平面图，为了证明平面图的一些性质，我们不得不用整章的数学语言，从平面几何和点集拓扑中，发展出所需要的概念。好消息是，有另一种只使用离散数学的方式来定义平面图。特别是,我们可以把平面图定义为递归数据类型。

13.2.1 面

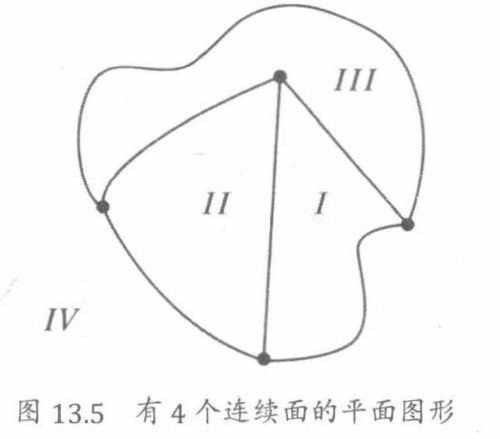
平面图形中的曲线将平面分割为连通区域，称其为连续面。

例如：图13.5所示的图形有4个连续面。无限延伸到各个方向的面IV被称为外表面。

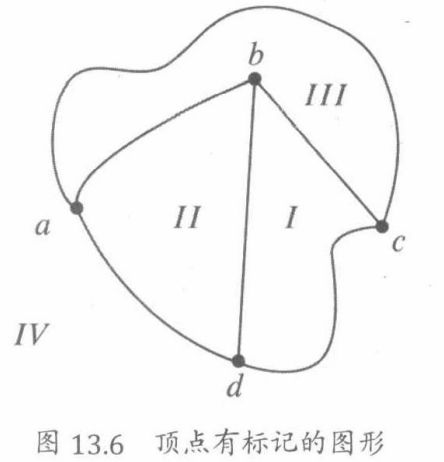
如果我们把各个顶点标上字母，每个连续面上边界上得圈我们可以进行如下的描述。

​ $abca$ $abda$ $bcdb$ $acda$

我们将上文中的圈称作图13.6中的离散面

我们使用术语“离散”是因为图中的圈是一个离散的数据类型，与平面上的区域即一个连续的数据类型相对。

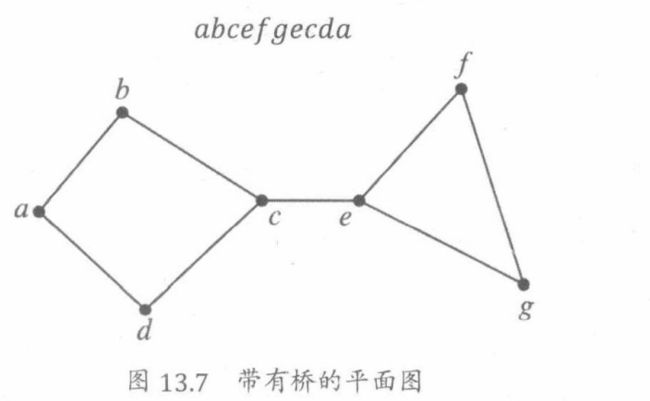
但是，平面图形中的连续面不总是被图中的圈所限制。

如下图的我们称之为桥的那部分

此序列定义了一个回路，但没有定义一个圈，这是因为桥和它的端点在路中出现了两次。

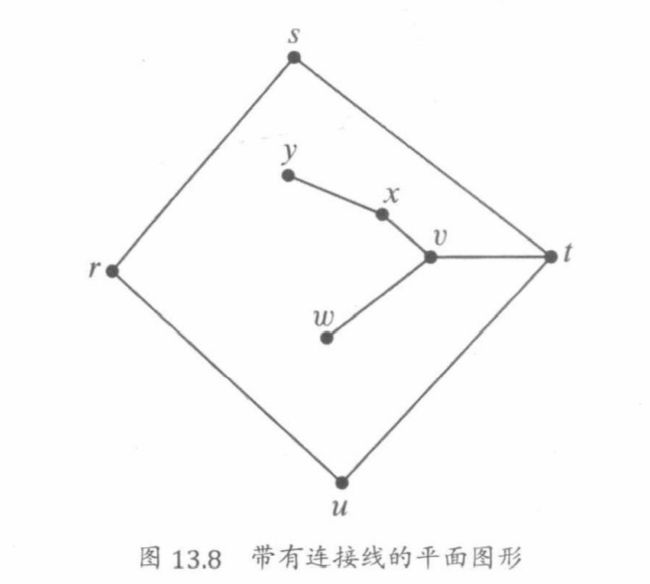
图13.8所示的平面图形展示了另外一个问题，即这幅图中的节点v,x, y,w和与之相连的边,我们称之为连接线。沿着内部区域边界的顶点序列是:
$$rstvxyxvwvtur$$
这个序列定义了一个回路，但也没有定义一个圈，这是因为每个连接线上的边都经过了两次——一次“来”和一次“回”。

至少对于连通图来说，我们发现桥和连接线是唯一的问题。特别是,在平面图形中每一个连续面在图中都对应于一个回路。这些回路被称为图形的离散面，接下来，我们要给它们下一个定义。

13.2.2 平面嵌入的递归定义

我们将连通图的平面嵌入定义为回路的集合，回路的集合是它的面边界。

定义13.2.2：连通图的平面嵌入包含图的一个非空回路集合,称这些回路为平面嵌入的离散面。平面嵌入的递归定义如下。

基本情形：如果G是由单个顶点v组成的图，那么G的平面嵌入有一个离散面，即长度为零的回路v。

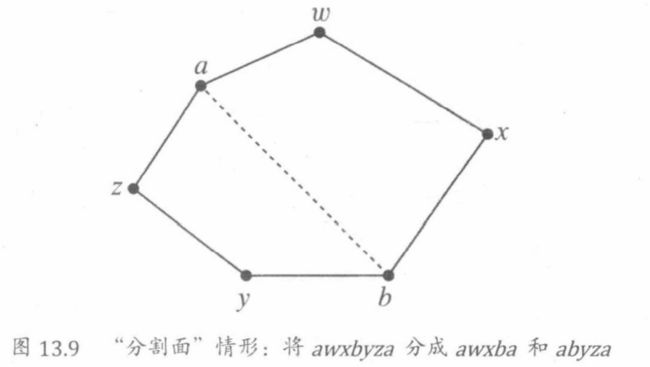
构造情形（分割一个面):假设G是一个有平面嵌入的连通图，并假设a和b是G的平面嵌入的某个离散面y上的、不同且不相邻的顶点。如果添加边到图G上，图上的平面嵌入会发生如下的变化

{azybxwa} → {azybxwa，azyba，abxwa}

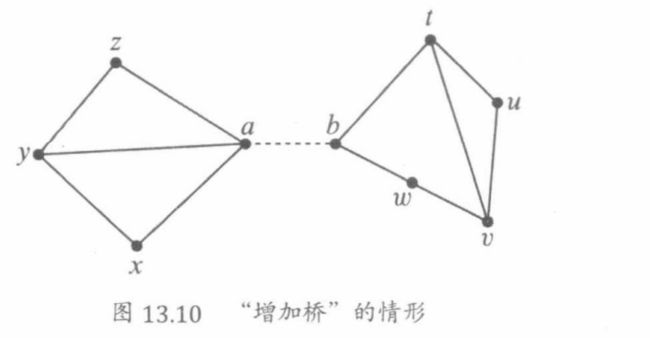
构造情形(增加一个桥)：假设G和H是有平面嵌入和不相交的顶点集合的连通图。

在连接a,b前，G和H的顶点序列为：

连接之后的顶点序列为：

一个桥是一个简单的切割边，但在平面嵌入的环境下，这些桥恰好是在同一个离散面上出现两次的边，而不是分别在两个面上各出现一次。连接线是由桥组成的树状图，我们只在示意图中使用连接线，因此没有必要更准确地定义它。

13.2.3 这个定义可行吗

是的！一般来说，根据定义13.2.1，一个图是平面的，当且仅当它有一个平面图形，且平面图形的每一个连通分量有一个如定义13.2.2所述的平面嵌入。

13.2.4：外表面在哪里呢

每一个平面图都有一个可立即识别的外表面，就是向四面八方无限延伸的那一个。但平面嵌人的外表面在哪里呢?

一个也没有！那是因为真的没有必要去区分一个面和另一个面。事实上，一个平面嵌入的任何面都能被画在外面。

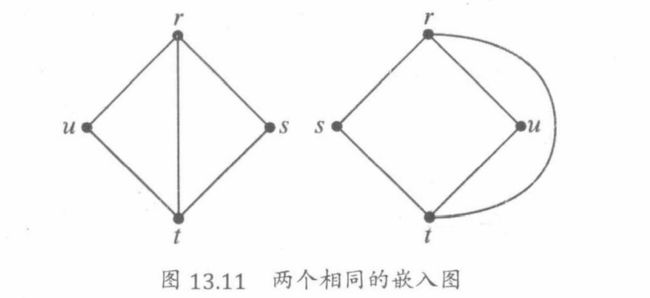
因此，显示不同的“外部”边界的图片可能实际上是有相同平面嵌入的图。例如，图13.11所示的两个嵌入是相同的——观察一下它们:它们有同样的边界圈。

下述是证明定理13.2.2中“增加桥”的情形:无论如何选择每个不相交平面图的嵌入的面,我们都可以在它们之间画一个桥，而不需要跨越图形中的任何其他边，因为我们可以假设桥接两个外表面。

13.3 欧拉公式

递归定义的价值在于，它提供证明平面图性质的强大技术，即结构归纳。例如，我们可以证明如下性质：

定理13.3.1：（欧拉公式）如果一个连通图有一个平面嵌入，那么
v- e + f = 2
这里，v代表顶点数量,e代表边的数量，f代表面的数量。

证明.：证明是对平面嵌入的定义做结构归纳法。令P($\epsilon$)为嵌入$\epsilon$能够满足v- e+ f = 2的命题。

基本情形：($\epsilon$是单个顶点的平面嵌入):根据定义,v = 1, e = 0, f = 1,并且1-0+1=2,所以P($\epsilon$)确实成立。

归纳步骤（分割一个面)：假设G是一个存在平面嵌入的连通图，并且假设a和b是G图中不同的、不相邻的顶点,且出现在平面嵌入的离散面$\gamma$ = a…b…a上。

通过加入边(a - b)到G的边中所得到的图，它的平面嵌入比G多一个面和一条边。所以两个图v - e + f的值保持不变，由于根据结构归纳法，对G的嵌入这个值是2，那么对G加一条边的嵌入也是2。所以P在新构造的嵌入中适用。

归纳步骤（增加一个桥)：假设G和H是有平面嵌入和不相交的顶点集合的连通图。那么用一个桥连接这两个图，会将这两个被桥接的面融合为一个面，并保持其他面不变。但是还会多一条边。

所以，对构造的嵌入，( v - e+f)恒等于2。也就是说，P($\epsilon$)在这种情况下也成立。

这就完成了归纳步骤的证明,并且定理遵循结构归纳法。

13.4 平面图中边的数量限制

引理13.4.1：在一个连通图的平面嵌入中，每条边在每两个不同的面上出现一次,或者恰好在一个面上出现两次。

引理13.4.2：在至少有3个顶点的连通图的平面嵌入中，每个面的长度至少为3。

结合引理13.4.1、13.4.2和欧拉公式，我们可以证明平面图中边的数量有一个限制,

引理13.4.3 ：假设一个连通平面图有v≥3个顶点和e条边。那么

证明.：根据定义，一个连通图是平面的当且仅当它有一个平面嵌入。所以假设一个连通图有v个顶点和e条边，以及一个有f个面的平面嵌入。根据引理13.4.1，每条边恰好在面边界上出现两次。所以面边界的长度之和恰好是2efont>。同样根据引理13.4.2，当v≥3时,每个面边界的长度至少为3，所以总和至少为3f。这意味着:

13.5 返回到$K_5$和$K_{3,3}$

一个完全图$K_5$是否是平面图，而通过定理13.4.3可以直接得出如下推论。

推论13.5.1: $K_5$不是平面图。

证明：$K_5$是有5个顶点和10条边的连通图。但是因为10>3·5-6,所以$K_5$不满足所有平面图应该满足的不等式13.3。

引理13.5.2：在至少有3个顶点的连通二分图的平面嵌入中，每个面的长度至少为4。

证明：由引理13.4.2可得，图的平面嵌入的每个面的长度至少为3。但是根据引理12.6.2和定理12.8.3，二分图不可能有奇数长度的回路。所以每一个面的长度至少是4。

定理13.5.3：假设一个顶点数v≥3、边数为e的连通二分图是平面的。那么

推论13.5.4：$K_{3,3}$不是平面的。

证明：$K_{3,3}$是连通二分图,有6个顶点和9条边。但是由于9>2·6一4，所以$K_{3,3}$不满足所有二分平面图应该满足的不等式13.3。

13.6 平面图的着色

我们介绍了平面图的很多方面，但这不足以证明著名的4-色定理，不过我们已经做了足够多的工作来证明每个平面图可以只用5个颜色着色。

引理13.6.1：平面图的每一个子图都是平面图。

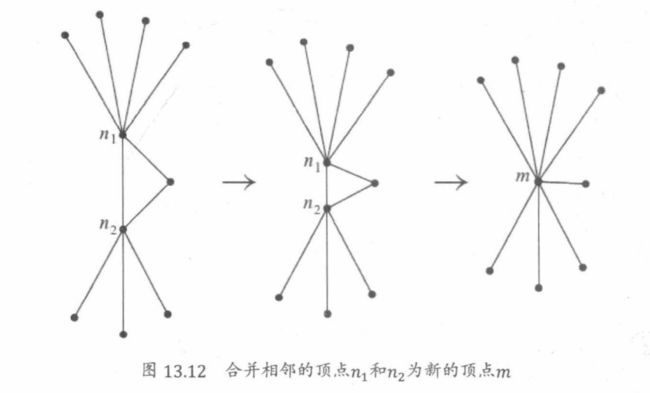
引理13.6.2：合并平面图的相邻顶点可得到另一个平面图。

引理13.6.3 ：每个平面图都有一个度不大于5的顶点。

定理13.6.4：任意一个平面图是可以5-着色的。

基本情形(v≤5)：显然成立。

归纳步骤：假设G是一个顶点数为v+1的平面图。我们描述一个5-着色的G。首先，选择图G中一个度数不超过5的顶点g。

情形1 ( deg(g)<5)：从G中删除g，根据引理13.6.1会得到一个平面图H，并且由于H具有v个顶点，通过归纳假设，它是可以5-着色的。因为g的度小于5，所以g一定可用与他相邻节点不相同的颜色去着色。

情形2( deg(g) = 5)：如果图G中g的5个邻居是互相邻接的,则这5个顶点将非平面子图。所以一定有g的两个邻居节点$n_1$和$n_2$，是不相邻的。现在将$n_1$和g合并成一个新的顶点m。我们可以将m和$n_2$合并为另一个新的顶点m’，从而产生一个新的图G’。由于G’有v-1个顶点，从归纳假设可知它是5-着色的。现在定义一个图G的5-着色如下，对图G’的除了顶点g,$n_1$和$n_2$,之外的所有顶点进行5-着色,然后将G’中的顶点m’的颜色分配给g的邻居$n_1$和$n_2$。因为在图G中,$n_1$和$n_2$不是相邻的，这定义了图G的一个除了点g之外的合理的5-着色。但是因为顶点g的两个邻居具有相同的颜色，g的邻居已经使用少于5种颜色进行着色,所以通过将5种颜色中不与顶点g的邻居相同的另外一种颜色分配给顶点g，就完成了图G的5-着色。

13.7 多面体的分类

一个多面体是由有限个多边形面所界定的、凸的三维区域。如果这些面是相同的正多边形，并且在每个角处有相同数量的多边形汇聚，则称多面体是正的。

我们可以通过考虑可平面性来确定有多少正多面体。可以把多面体的边投影到球体上，这将给出一个平面图嵌入到球体上的像，多面体的角的像对应于图的顶点。通过实验观察得出，球面上的嵌入与平面上是相同的，因此，平面图上的欧拉公式可以指导我们找到正多面体。

设m为多面体每个角处汇聚的面的数目，n为每个面的边数。在相应的平面图中，有m条边分别连接到v个顶点。根据握手引理12.2.1，我们可得出:

并且,每个面都包括n条边。又因为每条边都与两个面相邻,就有nf = 2e ,求解等式中的v和f ,带入欧拉公式可得

化简得：

m和n的取值范围是 3<=m,n<=6。

13.8 平面图的另一个特征

定理13.8.1：一个图是非平面的当且仅当它以K,和K3,3为最小集。

定义13.8.2：一个图G的最小集依然是一个图，它可通过重复删除顶点、删除边，以及合并图G的相邻顶点来获得。