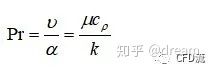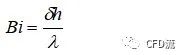【力学】关于力学的一些基础知识

学习笔记——各种需要补充的知识

1. 色散、耗散、扩散

1. 数值耗散：耗散是能量的损失。耗散和扩散是相关联的，扩散是物质向四周飘散的现象，所以正是因为有色散才有耗散，这就说明了扩散和耗散是相关的。（偶数阶导数）

2. 数值色散: 是一种与波有关的波动现象。每个阵型的传播速度相同，那就说明是无色散的。在数值中，波动方程$$u_t+a{u}_x=0,u_{tt}=a^2{u}_{xx}$$就是无色散的，而$$u_t=u_{xxx}$$就是色散方程。（奇数阶导数）

3. 但是数值算法作为模拟宏观方程的一个工具，本身会使得没有耗散色散的宏观方程变成带耗散项和色散项的数值方程，所以我们关注的角度就是用不同的数值方法，来增加模拟的精度，降低算法的误差。

4. 从数值的角度，我们谈的是耗散和色散。扩散是一种物理现象。

5. 耗散是因为扩散的出现导致的能量损失。色散是各个频率的波传播速度是否相同。

6. 记住一句话，色散考虑的是不同频率波的传播速度是否相同，耗散考虑的是能量的损失。

2.关于角点的处理

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fxMTDdpx-1609400670962)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20200829191450299.png)]

3.潜热

由低能状态转变为高能状态时吸收潜热, 反之则放出潜热。例如，液体沸腾时吸收的潜热一部 分用来克服分子间的引力，另一部分用来在膨胀过程中反抗大气压强做功。熔解热、汽化热 升华热都是潜热。潜热的量值常常用每单位质量的物质或用每摩尔物质在相变时所吸收或放出 的热量来表示。潜热的发生总会伴随着物贡相态的变化, 简单的理解就是水在沸腾的时候要吸 收很多的热量而温度没多大的变化。对液态的水加热, 水的温度升高, 当达到沸点时，呈然热 量不断的加入，但水的温度不升高, 一直停留在沸点, 加进的热量仅使水变成水蒸气, 即由液 态变为气态。 “潜热” 不能用温度计测量出来, 人体也无法感觉到，但可通过实验计算出来。 这种不改变物质的温度而引起物态变化(又称相变)的热量称为潜热。如计算机房中、工作人员 人体发热以及换气带进来的空气含湿量, 这些热量都为潜热。

4.各种无量纲数

• 雷诺数（Re）
• 努塞尔数（Nu）
• 普朗特数（Pr）
• 毕渥数（Bi）
• 傅里叶数（Fo）
• 马赫数（Ma）

01—雷诺数（Re）

英国物理学家老雷（雷诺）进行了大量的实验，并在1883年发表的报告中提出：自然界的流体流动有两种不同的流态，低速下为层流，流速增大后，流体流动过度为湍流（紊流）；在层流下流体的流动是有规则有秩序的，在湍流情况下，流体的运动是杂乱无章的。雷诺在大量实验的基础上，用所有影响流动状态因素的一个无因次组合数（雷诺数），来判断流动是层流还是湍流，定义为：

其中，ρ为流体密度，v为流体速度，l为特征长度，μ为动力粘度，υ为运动粘度

在工程实际中，一般当Re≤2000，认为管内的流动为层流；当Re>2000时，认为管内流动为湍流。

**雷诺数实际上表征的是：惯性力和粘性力之比。**当雷诺数较小时，流场中粘性力起主导作用，惯性力起次要作用；当雷诺数较大时，流场中惯性力起主导作用，粘性力起次要作用。

02—努塞尔数（Nu）

努塞尔数（Nusselt number），以德国物理学家威廉·努塞尔特（Wilhelm Nusselt）的名字命名，以纪念其对此方面研究的突破。努赛尔数的物理意义为是表示对流换热强烈程度的一个无量纲数。

其中，h为流体的对流传热系数，l为传热面的几何特征长度，k为流体的导热系数。

03—普朗特数（Pr）

普朗特数是流体力学中表征流体流动中动量交换与热交换相对重要性的一个无量纲参数，表明温度边界层和流动边界层的关系，反映流体物理性质对对流传热过程的影响。记为Pr。

υ为运动粘度，α为热扩散系数，μ为动力粘度，c_ρ为比热容，k为导热系数。

当几何尺寸和流速一定时，流体粘度大，流动边界层厚度也大；流体导温系数大，温度传递速度快，温度边界层厚度发展得快,使温度边界层厚度增加。因此，普朗特数的大小可直接用来衡量两种边界层厚度的比值。

04—毕渥数（Bi）

表征固体内部单位导热面积上的导热热阻（内部热阻）与单位面积上的换热热阻（即外部热阻）之比。

б是特征长度，h是表面传热系数，λ是导热系数。

Bi数越小，意味着内热阻越小或外热阻越大；Bi越大，意味着内热阻越大或外热阻越小。

05—傅里叶数（Fo）

傅里叶数可以理解为两个时间间隔相除所得的无量纲时间。

τ是从边界上开始发生热扰动的时刻起到所计算时刻为止的时间间隔，分母可以视为使边界上发生的有限大小的热扰动穿过一定厚度的固体扩散到l_c的面积上所需的时间。因此，Fo数可以看成是表征非稳态过程进行深度的无量纲时间。在非稳态导热过程中，这一无量纲时间越大，热扰动就越深入的传播到物体内部，因而物体内各点的温度越接近周围介质的温度。

06—马赫数（Ma）

流体力学中表征流体可压缩程度的一个无量纲参数，记为Ma，定义为流场中某点的速度v同该点的当地声速c之比，

亚声速不可压缩流：M<0.3

亚声速可压缩流：0.3≤M≤0.8

跨声速流：0.8≤M≤1.2

超声速流：1.2≤M≤5

高超声速流：M≥5

5.临界温度

使物质由气态变为液态的最高温度叫临界温度。每种物质都有一个特定的温度，在这个温度以上，无论怎样增大压强，气态物质都不会液化，这个温度就是临界温度。

1.液体能维持液相的最高温度叫临界温度。

2.物质处于临界状态时的温度。

3.物质以液态形式出现的最高温度。

4.高于临界温度，无论加多大压力都不能使气体液化。在临界温度时，使气体液化所必须的最低压力叫临界压力。

5.临界温度越低，越难液化。

6.热传导，热对流，热扩散

conduction 热传导 diffusion 热扩散(无量纲化的热传导)

convection 热对流

7.粘性系数

kinematic viscosity 运动学粘性系数。运动学粘性系数是用来衡量流体粘性大小的物理量，是流体的动力粘性系数μ与其密度ρ的比值。以符号γ表示，即$\nu$=μ/ρ，单位是m2/s，γ无特殊物理意义，因具有运动学的量纲，故称为运动学粘性系数。它表征的物理量是粘性力与惯性力之比。γ的数值取决于流体的性质、温度和压力。

dynamic viscosity 动力粘性系数。$\mu$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7v38MSrm-1609400670973)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20201102173543585.png)]

$\nu$:运动学粘性系数

$\mu$:动力学粘性系数

8. N-S方程

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yZd4LOeo-1609400670974)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20201029175606188.png)]

9. 原点矩和中心矩

l 原点矩的定义

随机变量ξ的k次幂ξ**k的数学期望称为ξ的***k***阶原点矩，**记为vk，

即vk=E(ξk*)*.

从而，对于离散随机变量，

对于连续随机变量，.

特别地，ξ的一阶原点矩就是ξ的数学期望.

l 中心矩的定义

随机变量ξ的离差的k次幂(ξ-Eξ)k的数学期望称为ξ的*k*阶中心矩，

记为μ_k，即μ_k=E(ξ-Eξ )^k.

从而，对于离散随机变量，

对于连续随机变量,.

特别地，ξ的一阶中心矩恒为零，二阶中心矩就是ξ的方差.

即μ1=0，μ2=D ξ.

l 原点矩与中心矩的关系

因为，故

特别地,

10.沸腾换热曲线

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mh73GoNO-1609400670979)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20201122192418229.png)]

1934 年， 日本科学家 Nukiyama[1]最先总结出了池式沸腾在不同阶段的特性， 并引入了沸腾曲线 （图 2 ） 的概念。起先在温度并不高的情况下， 热表面和冷却剂之间的换热靠热表面附近的高温流体与远离热表面的低温流体之间产生的自然对流。随着热表面温度的增高， 气泡逐渐在热表面生成并离开热表面， 传热能力也进一步增强。这个阶段就是核态沸腾传热阶段。当热表面温度继续升高， 越来越多的气泡产生并相互干扰和合并， 使得热表面热流密度到达一个极限值之后开始逐渐降低， 即传热能力增强到一个极限后就开始下降。这个核态沸腾区域的最大热流密度就是临界热流密度 （CHF ） ， 而因气泡的相互干扰和合并导致的热流密度下降区域称为过渡沸腾区。随着气泡相互干扰导致彼此合并得越来越多， 传热能力进一步下降， 最终会形成气膜覆盖整个热表面， 冷却剂和热表面完全分离开， 热交换主要靠热辐射来完成。综合比较四个沸腾阶段， 核态沸腾无疑是最安全也是传热效率最高的。因此在堆芯熔融工况下的应急冷却设计中， 需尽可能长的时间内让换热过程处于核态沸腾的状下。