决策树基本原理：基于信息增益、增益率与基尼系数的划分选择，预剪枝与后剪枝，多变量决策树以及决策树优缺点概述

一、基本流程

决策树算法是数据挖掘分类算法中常见的一种方法。它以树状结构表现，叶子结点代表分类结果，内部结点描述一个属性，从上到下的一条路径，确定一条分类规则。
[1]谢妞妞.决策树算法综述[J].软件导刊,2015,14(11):63-65.

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树。其名字由两部分构成，也代表了它的两个典型特点：

• 决策：决策树具有可解释性，这在辅助决策方面非常有用，在实际的决策行为中，不仅需要知道最终结果，最好还能知道得出这样结果的原因和过程。
• 树：树形结构有各种非常好的功能和特性，表达能力强。

决策树的一般过程的文字表述：

（1）首先，创建结点 $t$，初始情况下训练集中所有样本都与结点 $t$ 关联，记为$D_t$，将 $t$ 记为当前结点。
（2）如果当前结点 $t$ 中所有样本类别相同，则将该结点标记为叶子结点，并停止进一步分裂。接着处理其他非叶子结点。否则，进入下一步。
（3）为数据集 $D_t$选择分裂属性和分裂条件，根据分裂条件将$D_t$ 分裂为m个自己，为 $t$ 创建m个子节点，将分裂出的m个数据集分别与这m个结点关联。依次将每个结点设为当前结点，转到（2）处理，直至所有结点都被标记为叶子结点。

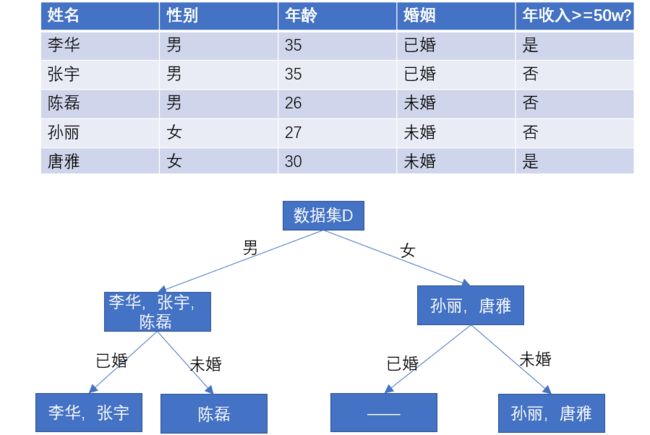
结合下面这个非常简易的例子可以更直观地理解，现在要根据这个数据集构建决策树，以根据一个人的性别、年龄、婚姻等属性判断他的年收入是否大于50w。要注意的是，分类属性的选择并不是随意的，其中有各种判定规则，后续会进行介绍。另外，根据决策树的递归过程，在处理完t1，创建好t3、t4后，未处理的结点有t2、t3、t4，但下一个当前结点应是t3或t4，而不会是t2.

这样一棵树数创建好后，如果有一个人：男，27，已婚，就会被判定为年收入大于50w。不过这个例子是非常简易的，可以看到年龄属性根本没用到，而一个女性，无论其年龄如何，婚姻状态如何，都会被认为年收入大于50w，这显然是不合理的。从中也可以看出，决策树的构建和数据集本身的特性有很大关系。如果我们第一个分类属性选的是年龄，那会因为有三个年龄值而创建3个子节点吗？或者选择一个年龄界限，比如30岁以上和30岁以下，可是这个界限怎么选择才合理呢？这都是后面要解决的问题。

---

西瓜书中的算法表述：

输入：训练集D = {(x1, y1), (x2, y2), (x3, y3),..., (xm, ym)};
      属性集A = {a1, a2,..., ad}.
过程：函数TreeGenerate(D, A)

1: 生成结点node;
2: if D中样本全属于同一类别C then
3:       将node标记为C类叶节点; return;
4: end if
5: if A = NULL OR D中样本在A上取值相同 then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if
8: 从A中选择最优划分属性a*;
9: for a*中的每一个值a*v do
10:       为node生成一个分支，令Dv表示D中在a*上取值为a*v的样本子集；
11:       if Dv为空 then
12:             将分支结点标记为叶结点，其类别标记为D中样本最多的类； return；
13:       else
14:             以TreeGenerate(Dv, A\{a*})为分支结点
15:       end if
16: end for

显然，决策树的生成是一个递归过程，有三种情形导致递归返回

• 1.当前结点所包含的样本都属于同一类别，无需划分
  • 做法： 将当前结点标记为叶结点，并令该类别为结点的类别
• 2.所有的属性都已被使用，或所有样本在所有属性上取值相同，无法划分
  • 做法：将当前结点标记为叶结点，但将其类别设定为父结点所含样本最多的类别（利用当前结点的后验分布）
• 3.当前结点包含的样本集合为空，不能划分
  • 做法：将当前结点标记为叶结点，但将其类别设定为父结点所含样本最多的类别（把父结点的样本分布作为当前结点的先验分布）

我一开始也很疑惑，第二和第三种情况为什么会出现。其实是这样的，如下图所示，李华和张宇所有的属性值都相同，但是年收入的分类却不同，属于第二章情况。这种情况有时候是由于脏数据，数据不一致导致的，而有时候是符合实际情况的，例如性别年龄婚姻都一样但年收入天差地别简直太正常了，这是数据本身的不完全。而第三种情况是这样，如果我们首先按性别划分，然后按婚姻划分，发现女性的子集里全都是未婚的。

注意上述代码块的第9、10行，在当前结点上，对于属性“婚姻”的每一个值，即"已婚/未婚"，都要生产一个分支，所以在女性的子集中进一步划分“已婚”和“未婚”的样本子集。由于女性已婚是空集，该结点的类别标记为父结点中数量最多的那个。

也就是说，对当前结点按某一属性进行划分时，属性的取值集合是看整个数据集中所有样本的值，而不是只看当下的子集。否则，就不会有“女——已婚”的分支，那么如果测试数据中有一个女性已婚样本，决策树就无法做出判断。

9： for a*中的每一个值a*v do
10:       为node生成一个分支，令Dv表示D中在a*上取值为a*v的样本子集；

二、划分选择

如何选择最优点划分属性？一般我们希望，决策树的分支结点所包含的样本尽可能属于同一类别，即结点的纯度(purity)越来越高。 所以，选择划分属性就是看：按照哪一个属性进行划分能使结点的纯度升高的程度最大。

1. 信息增益（ID3算法）

ID3算法是一个从上到下、分而治之的归纳过程。 ID3算法选择具有最高信息增益的属性作为测试属性。

首先，“纯度”要用什么指标来衡量呢？信息熵（information entropy） 是度量样本集合纯度最常用的一种指标。假定当前样本集合 $D$ 中第k类样本所占的比例为 $p_k(k=1,2,...,n)$ 则 $D$ 的信息熵定义为 $$Ent(D)=-\sum _{k=1}^n{p}_{k}lo{g}_2{p}_k$$ 注：
（1）$p=0$，则 $plo{g}_{2}p=0$
（2）$Ent(D)$ 最大为 $lo{g}_{2}n$，最小为 0。
（3）$Ent(D)$越小，则 $D$ 纯度越高。

信息熵是怎么度量纯度的呢？集合纯度是怎么影响熵值变化的呢？了解“熵”的原始含义以及熵是如何引入信息论的将有助于进行理解。
1、从熵到信息熵，熵在不同领域的含义
2、熵的引入与各种不同的熵

假设数据集 $D$ 中所有样本都是同一类别，$Ent(D)=0$；

如果有两个类别，且个数相等，则 $Ent(D)=-\frac{1}{2}lo{g}_2\frac{1}{2}-\frac{1}{2}lo{g}_2\frac{1}{2}=1$ ；

若每个样本都各自为一个类别，一共有n个类别，则 $Ent(D)=n(-\frac{1}{n}lo{g}_2\frac{1}{n})=lo{g}_{2}n$

可以看出，随着集合中样本类别增多，纯度下降，信息熵也越来越大。

---

介绍完信息熵，就可以介绍信息增益了。简单地说，信息增益就是信息熵的减小值，是纯度提升的程度。信息增益的计算公式： $$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$ 其中，$a$指某一个离散属性，它有$V$个可能的取值，按照这$V$个取值划分出$V$个子集，将第$v$个子集记为$D^v$，$Gain(D,a)$指数据集$D$按属性$a$划分的信息增益。信息增益就是【原来的信息熵】减去【按某属性划分后所有子集的信息熵的期望值】 信息增益越大，则意味着使用属性a划分所获得的纯度提升越大。ID3算法就是以信息增益为准则来进行划分的。

2. 信息增益率(C4.5算法)

信息增益准则其实是有一些问题的，它会更倾向于选择【取值数目较多的属性】，若有一个属性是“编号”，那么每个编号都是不同的，按编号来划分得到的每个子集只包含一个样本，划分后所有子集的信息熵的和为0，信息增益肯定最大，但是这样划分是没有意义的，所产生的决策树不具有泛化能力。

C4.5算法则不直接使用信息增益，而是使用增益率：$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$ $$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$其中，$IV(a)$ (intrinsic value)是属性a的固有值，属性a的取值越多，该值就越大。其计算式和信息熵的计算其实是一样的，相当于将属性a看作信息熵计算时的分类属性。

增益率对取值较少的属性有偏好，所以C4.5使用了一种启发式算法：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

3. 基尼指数(CART)

数据集 $D$ 的纯度用基尼值来度量，它反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率，基尼值越小，数据集的纯度越高：$$Gini(D)=\sum _{k=1}^n\sum _{k^{{}^{\prime }}\ne k}{p}_k{p}_{k^{{}^{\prime }}}=1-\sum _{k=1}^n{p}_k^2$$属性a的基尼指数定义为：$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$CART决策树就是采用基尼指数来选择划分属性的，选择那个划分后使得基尼指数最小的属性作为最优划分属性。

CART（classification and regression tree 分类与回归树）可以处理高度倾斜或多态的数值型数据, 也可处理顺序或无序的类属型数据。CART算法采用2分递归划分, 在分支节点上进行布尔测试, 判断条件为真的划归左分支, 否则划归右分支, 最终形成一棵二叉决策树。由于二叉树不易产生数据碎片, 精确度往往高于多叉树。

4. 举例计算

现在具体的数据集上进行计算，以熟悉各种属性选择方式的操作过程，对公式有一个更加清晰直观的认识。如图所示的数据集，有年龄、性别、年收入、婚姻四个属性，并根据是否购买豪华车分为了两类。其中，年收入是连续值属性。下面以“性别”为例分别计算信息增益、信息增益率、基尼指数，并在最后介绍连续值属性的处理。

（1）信息增益

计算“性别”属性的信息增益，首先要计算数据集的信息熵。根据是否购买豪华车分为两类，购买的有5人，未购买有9人，因此：$$Ent(D)=-\sum _{k=1}^n{p}_{k}lo{g}_2{p}_k=-\frac{5}{14}lo{g}_2\frac{5}{14}-\frac{9}{14}lo{g}_2\frac{9}{14}=0.531+0.410=0.941$$
根据性别，可以把数据集划分成两个子集，对于$D_{女}$，2/7买了豪华车，5/7未买；对于$D_{男}$，3/7买了豪华车，4/7未买。

$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)=0.941-\frac{7}{14}(-\frac{2}{7}lo{g}_2\frac{2}{7}-\frac{5}{7}lo{g}_2\frac{5}{7})-\frac{7}{14}(-\frac{3}{7}lo{g}_2\frac{3}{7}-\frac{4}{7}lo{g}_2\frac{4}{7})$$

（2）信息增益率

在计算了信息增益的基础上，还需要计算$IV(性别)$ $$IV(性别)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}=-\frac{7}{14}lo{g}_2\frac{7}{14}-\frac{7}{14}lo{g}_2\frac{7}{14}=1$$ 在本例中，$$Gain\_ratio(D,性别)=\frac{Gain(D,性别)}{IV(性别)}=Gain(D,性别)$$

（3）基尼系数

$$Gini\_index(D,性别)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)=\frac{7}{14}(1-\frac{2}{7}\cdot \frac{2}{7}-\frac{5}{7}\cdot \frac{5}{7})+\frac{7}{14}(1-\frac{3}{7}\cdot \frac{3}{7}-\frac{4}{7}\cdot \frac{4}{7})$$

（4）连续值属性的处理

最后，以年收入为例介绍连续值属性的处理。 对于连续值属性，需要选择一个划分点，比如，可以选100万为划分点，将年收入划分为大于100万的和小于100万的，把连续属性转化为类别属性之后按上述一样操作即可。但是划分点可以有很多种选择，一般选信息增益最大的那个，这样就需要计算很多次很麻烦。稍微简便一点的做法是，将数据升序或降序排列后，只计算分类结果变化时的划分点。

举例来说，将数据按照年收入从小到大排列：

首先取20和40的中点30，以30作为年收入的划分，但是20和40对应的样本都是未购买豪华车，分类标签不变，因此省略计算。
选取40和50的中点45，以45作为年收入的划分，40和50对应的样本类别不同，一个是未购买，一个是购买，因此需要计算信息增益。
以此类推，还要分别以57.5、81、84、90.5、94、148为分界点，计算年收入属性的信息增益，并选择信息增益最高的那个划分方式。

要注意的是，连续属性使用过后，还可以作为后代结点的划分属性，如在父结点使用了“年龄<=30”,在子节点上还可以使用“年龄<=20”

（5）缺失值的处理

这一篇博文讲得非常清晰具体，我就偷个懒了：决策树缺失值的处理

---

三、剪枝优化

决策树学习的过程中，可能会产生过拟合，这是因为将训练数据自身的一些性质当成了所有数据集的一般性质。造成过拟合的原因有很多，学得太具体了、数据量太少、噪声数据对决策边界的影响……因此，可以通过主动去掉一些分支来降低过拟合风险，其基本策略有“预剪枝”和“后剪枝”。

	预剪枝	后剪枝
做法	在决策树生成过程中，对每个结点划分前先估计，若不能带来泛化性能提升，则停止划分并标记为叶结点。	先生成完整决策树，再自底向上对非叶结点进行考察，若替换成叶结点能带来性能提升则将子数替换为叶结点。
优点	①降低过拟合风险 ②减少训练和测试的时间开销	有更多的分支，欠拟合风险小，泛化性能往往优于预剪枝。
缺点	有些分支导致泛化性能暂时下降，但后续划分能显著提高，而“贪心”本质禁止这些分支展开，带来欠拟合风险	训练时间开销大

• 如果剪枝之后泛化性能不变，根据奥卡姆剃刀原理也应当使用剪枝之后的结果。

四、多变量决策树

若我们把每个属性视为坐标空间中的一个坐标轴，则d个属性描述的样本就对应了d未控件的一个数据点，对样本分类就是在这个坐标控件中寻找不同类样本之间的分类边界。

决策树形成的分类边界的特点：轴平行axis-parallel——分类边界的每一段都是与坐标轴平行的，者具有很好的可解释性，但是在真实分类边界比较复杂时，必须使用多段划分才能获得较好的近似。

而多变量决策树就可以实现“斜划分”或更复杂的划分，非叶结点不再是仅对某个属性，而是对属性的线性组合进行册数，即每个非叶结点都是一个形如 ${\sum }_{i=1}^d{w}_i{a}_i=t$ 的线性分类器，$a_i$是属性，$w_i$和 $t$可以通过当前结点所含的样本集和属性集学到。

五、另一种描述——经验熵、经验条件熵

设 $X$ 是一个取有限个值的离散随机变量，其概率分布为$$P(X=x_i)=p_i,i=1,2,...,n$$ 则随机变量$X$的熵定义为$$H(X)=-\sum _{i=1}^n{p}_{i}log{p}_i$$ 底数可以是2也可以是e，不同的底数熵的单位也不同。熵的大小只依赖于$X$的分布，与$X$的取值无关。

条件熵是在已知随机变量X的条件下随机变量Y的不确定性。$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$当熵中的概率由数据估计(特别是最大似然估计)得到时，所对应的熵称为经验熵和经验条件熵。

特征 $a$ 对数据集 $D$ 的信息增益$Gain(D,a)$也就是数据集的经验熵$H(D)$与特征 $a$给定条件下$D$的经验条件熵$H(D|a)$之差：$$Gain(D,a)=H(D)-H(D|a)$$ 表示由于特征 $a$ 而使得对数据集的分类的不确定性减少的程度。信息增益等价于互信息。

这里插个旗，打算另写一篇总结一下各种熵，自信息互信息等等

---

六、决策树优缺点

1. 优点

• 可解释性强，树结构能够可视化，可以生成容易理解的规则
• 训练所需要的数据少，且不需要进行数据规范化
• 使用效率高，使用决策树的开销是训练所需数据点的对数
• 能处理连续型和离散型数据
• 通常不需要训练数据之外的先验知识或领域知识

2. 缺点

• 忽略属性之间的相关性

如果实际数据中只需要一条规律:“属性A的值比属性B的值大的时候, 输出为1, 否则为0”的话, 决策树无法给出这样的规律, 因为它只会尝试属性A和某个常数的比较。

• 容易产生一个过于复杂的模型（过拟合）
• 在某些类别占主导地位的不平衡数据中，会学得一个有偏差的树。

---

附：sklearn官方文档对决策树优缺点的介绍， 加了我自己的翻译，如有不当烦请指出。

Some advantages（优点） ofdecision trees are:

---

（1）Simple to understand and to interpret. Trees can be visualised. 容易理解和解释，树结构可以可视化。

.
（2）Requires little data preparation. Other techniques often require data normalisation, dummy variables need to be created and blank values to be removed. Note however that this module does not support missing values. 通常不需要数据预处理，而一些其他的算法通常需要进行规范化，生成虚拟变量，空值移除。需要注意的是，决策树不能处理缺失值。
*[1]杨剑锋,乔佩蕊,李永梅,王宁.机器学习分类问题及算法研究综述[J].统计与决策,2019,35(06):36-40.DOI:10.13546/j.cnki.tjyjc.2019.06.008. *

.
（3）The cost of using the tree (i.e., predicting data) is logarithmic in
the number of data points used to train the tree. 使用效率高，使用决策树的开销是训练所需数据点的对数。
.

（4）Able to handle both numerical and categorical data. However
scikit-learn implementation does not support categorical variables for
now. Other techniques are usually specialised in analysing datasets
that have only one type of variable. 能够处理数值型和类别型数据。然而sklearn的决策树实现目前不支持类别型变量。
.
（5）Able to handle multi-output problems. 能够处理多值输出问题。
.
（6）Uses a white box model. If a given situation is observable in a model, the explanation for the condition is easily explained by boolean logic. By contrast, in a black box model (e.g., in an artificial neural network), results may be more difficult to interpret. 使用白盒模型。如果某种给定的情况在模型中是可以观察的，那么就可以轻易的通过布尔逻辑来进行解释，相比之下在黑盒模型（如人工神经网络）中的结果就是很难说明清楚。
.
（7）Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model. 可以用统计检验来验证模型，这使得解释模型的可靠性有可能被解释。
.
（8）Performs well even if its assumptions are somewhat violated by the true model from which the data were generated. 即使它的假设违背了产生数据的真实模型，决策树的效果也很好。
.
The disadvantages（缺点） of decision trees include:

---

（1）Decision-tree learners can create over-complex trees that do not generalise the data well. This is called overfitting. Mechanisms such as pruning, setting the minimum number of samples required at a leaf node or setting the maximum depth of the tree are necessary to avoid this problem.决策树学习器会生成过于复杂的树从而不能很好的概括数据，这就是过拟合。有必要通过剪枝、设置最小叶结点中的样本个数、设置最大深度的方法避免这个问题。
.
（2）Decision trees can be unstable because small variations in the data might result in a completely different tree being generated. This problem is mitigated by using decision trees within an ensemble.
决策树是不稳定的，训练数据的微小变化可能导致生成完全不同的树，这可以通过集成学习进行缓解。
.
（3）Predictions of decision trees are neither smooth nor continuous, but piecewise constant approximations as seen in the above figure. Therefore, they are not good at extrapolation.决策树的预测既不是平滑的也不是连续的，而是分段近似。因此，它们不擅长外推。
.
（4）The problem of learning an optimal decision tree is known to be NP-complete under several aspects of optimality and even for simple concepts. Consequently, practical decision-tree learning algorithms are based on heuristic algorithms such as the greedy algorithm where locally optimal decisions are made at each node. Such algorithms cannot guarantee to return the globally optimal decision tree. This can be mitigated by training multiple trees in an ensemble learner, where the features and samples are randomly sampled with replacement.
学习最优决策树的问题是一个NP完全问题。因此，实际的决策树学习算法基于启发式算法，例如贪婪算法，在每个节点上做出局部最优决策。这种算法不能保证返回全局最优决策树。这可以通过在集成学习器中训练多棵树来缓解，其中对特征和样本随机抽样。
.

（5）There are concepts that are hard to learn because decision trees do not express them easily, such as XOR, parity or multiplexer problems.
有一些概念难以学习，因为决策树不能很好地解释它们，例如，异或问题, parity or multiplexer problems.
.
（6） Decision tree learners create biased trees if some classes dominate. It is therefore recommended to balance the dataset prior to fitting with the decision tree. 如果某些分类占优势，决策树将会创建一棵有偏差的树。因此，建议使用平衡的数据训练决策树。