大数据时代的采样定理：马尔可夫链蒙特卡洛(MCMC)与其python实现

大数据时代的特点是数据除了数量多、维度也将变多。那么传统的采样定理如果要构造合适的概率分布函数耗时且耗费大量算力。
因此引入马尔科夫链的遍历性（Ergodicity）、常返性（recurrency）特点以及蒙特卡洛方法的大量实验逼近真实概率分布的原理实现多维的数据采样。从而构造概率分布函数。
假设我们要采样的是一个二维正态分布 N（U,SIGMA），其中： U=（5，-1）， 方差sigma=（1,1
1,4 ）;

而采样过程中的需要的状态转移条件分布为：

from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal

samplesource = multivariate_normal(mean=[5,-1], cov=[[1,0.5],[0.5,2]])

def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * s2 / s1 * (x - m1), math.sqrt(1 - rho ** 2) * s2))

def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * s1 / s2 * (y - m2), math.sqrt(1 - rho ** 2) * s1))

N = 5000
K = 20
x_res = []
y_res = []
z_res = []
m1 = 5
m2 = -1
s1 = 1
s2 = 2

rho = 0.5
y = m2

for i in range(N):
    for j in range(K):
        x = p_xgiveny(y, m1, m2, s1, s2)   #y给定得到x的采样
        y = p_ygivenx(x, m1, m2, s1, s2)   #x给定得到y的采样
        z = samplesource.pdf([x,y])
        x_res.append(x)
        y_res.append(y)
        z_res.append(z)

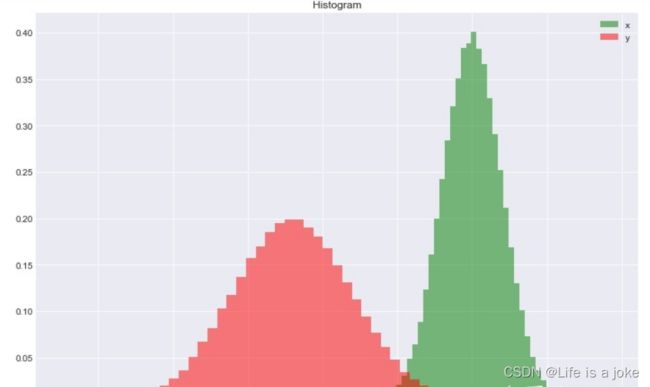
num_bins = 50
plt.hist(x_res, num_bins, normed=1, facecolor='green', alpha=0.5,label='x')
plt.hist(y_res, num_bins, normed=1, facecolor='red', alpha=0.5,label='y')
plt.title('Histogram')
plt.legend()
plt.show()

即实现了以上对于X和Y之间相互的条件概率分布。因此我们可以得到下一步空间分布：

ig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(x_res, y_res, z_res,marker='o')
plt.show()

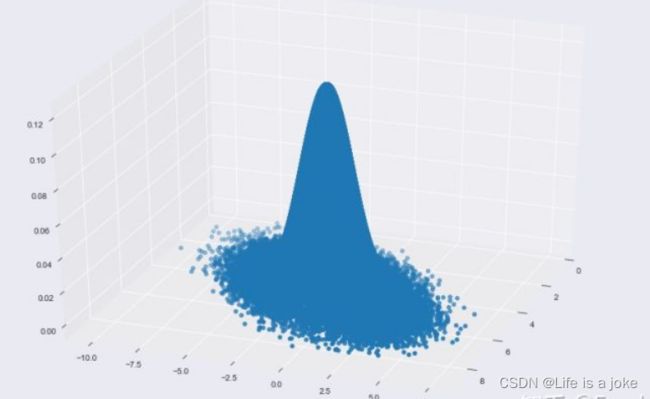
以上采样方法叫做GIbbs采样。由于Gibbs采样在高维特征时的优势，目前我们通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的,这时M-H采样仍然成立。

有了Gibbs采样来获取概率分布的样本集，有了蒙特卡罗方法来用样本集模拟求和，他们一起就奠定了MCMC算法在大数据时代高维数据模拟求和时的作用。