图神经网络库DGL使用指南

第1章：图

图表示实体(节点)和它们的关系(边)，其中节点和边可以是有类型的 (例如，“用户” 和 “物品” 是两种不同类型的节点)。 DGL通过其核心数据结构 DGLGraph 提供了一个以图为中心的编程抽象。 DGLGraph 提供了接口以处理图的结构、节点/边 的特征，以及使用这些组件可以执行的计算。

本章路线图

本章首先简要介绍了图的定义（见1.1节），然后介绍了一些 DGLGraph 相关的核心概念：

1.1 关于图的基本概念

1.2 图、节点和边

1.3 节点和边的特征

1.4 从外部源创建图

1.5 异构图

1.6 在GPU上使用DGLGraph

1.1 关于图的基本概念

图是用以表示实体及其关系的结构，记为 G=(V,E) 。图由两个集合组成，一是节点的集合 V ，一个是边的集合 E 。 在边集 E 中，一条边 (u,v) 连接一对节点 u 和 v ，表明两节点间存在关系。关系可以是无向的， 如描述节点之间的对称关系；也可以是有向的，如描述非对称关系。例如，若用图对社交网络中人们的友谊关系进行建模，因为友谊是相互的，则边是无向的； 若用图对Twitter用户的关注行为进行建模，则边是有向的。图可以是 有向的 或 无向的 ，这取决于图中边的方向性。

图可以是 加权的 或 未加权的 。在加权图中，每条边都与一个标量权重值相关联。例如，该权重可以表示长度或连接的强度。

图可以是 同构的 或是 异构的 。在同构图中，所有节点表示同一类型的实体，所有边表示同一类型的关系。 例如，社交网络的图由表示同一实体类型的人及其相互之间的社交关系组成。

相对地，在异构图中，节点和边的类型可以是不同的。例如，编码市场的图可以有表示”顾客”、”商家”和”商品”的节点， 它们通过“想购买”、“已经购买”、“是顾客”和“正在销售”的边互相连接。二分图是一类特殊的、常用的异构图， 其中的边连接两类不同类型的节点。例如，在推荐系统中，可以使用二分图表示”用户”和”物品”之间的关系。想了解更多信息，读者可参考 1.5 异构图。

在多重图中，同一对节点之间可以有多条（有向）边，包括自循环的边。例如，两名作者可以在不同年份共同署名文章， 这就带来了具有不同特征的多条边。

1.2 图、节点和边

DGL使用一个唯一的整数来表示一个节点，称为点ID；并用对应的两个端点ID表示一条边。同时，DGL也会根据边被添加的顺序， 给每条边分配一个唯一的整数编号，称为边ID。节点和边的ID都是从0开始构建的。在DGL的图里，所有的边都是有方向的， 即边 (u,v) 表示它是从节点 u 指向节点 v 的。

对于多个节点，DGL使用一个一维的整型张量（如，PyTorch的Tensor类，TensorFlow的Tensor类或MXNet的ndarray类）来保存图的点ID， DGL称之为”节点张量”。为了指代多条边，DGL使用一个包含2个节点张量的元组 (U,V) ，其中，用 (U[i],V[i]) 指代一条 U[i] 到 V[i] 的边。

创建一个 DGLGraph 对象的一种方法是使用 dgl.graph() 函数。它接受一个边的集合作为输入。DGL也支持从其他的数据源来创建图对象。 读者可参考 1.4 从外部源创建图。

下面的代码段使用了 dgl.graph() 函数来构建一个 DGLGraph 对象，对应着下图所示的包含4个节点的图。 其中一些代码演示了查询图结构的部分API的使用方法。

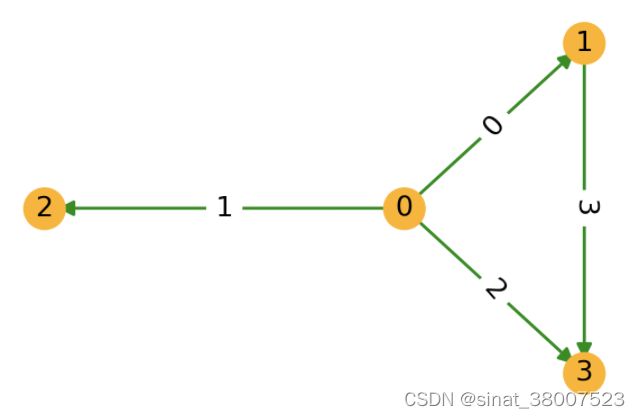
import dgl
import torch as th
# 边 0->1, 0->2, 0->3, 1->3
u, v = th.tensor([0, 0, 0, 1]), th.tensor([1, 2, 3, 3])
g = dgl.graph((u, v))
print(g) # 图中节点的数量是DGL通过给定的图的边列表中最大的点ID推断所得出的
# 获取节点的ID
print(g.nodes())
# 获取边的对应端点
print(g.edges())
# 获取边的对应端点和边ID
print(g.edges(form='all'))
# 如果具有最大ID的节点没有边，在创建图的时候，用户需要明确地指明节点的数量。
g = dgl.graph((u, v), num_nodes=8)

对于无向的图，用户需要为每条边都创建两个方向的边。可以使用 dgl.to_bidirected() 函数来实现这个目的。 如下面的代码段所示，这个函数可以把原图转换成一个包含反向边的图。

bg = dgl.to_bidirected(g)
bg.edges()

由于Tensor类内部使用C来存储，且显性定义了数据类型以及存储的设备信息，DGL推荐使用Tensor作为DGL API的输入。 不过大部分的DGL API也支持Python的可迭代类型(比如列表)或numpy.ndarray类型作为API的输入，方便用户快速进行开发验证。

DGL支持使用 32 位或 64 位的整数作为节点ID和边ID。节点和边ID的数据类型必须一致。如果使用 64 位整数， DGL可以处理最多 263−1 个节点或边。不过，如果图里的节点或者边的数量小于 263−1 ，用户最好使用 32 位整数。 这样不仅能提升速度，还能减少内存的使用。DGL提供了进行数据类型转换的方法，如下例所示。

edges = th.tensor([2, 5, 3]), th.tensor([3, 5, 0])  # 边：2->3, 5->5, 3->0
g64 = dgl.graph(edges)  # DGL默认使用int64
print(g64.idtype)
g32 = dgl.graph(edges, idtype=th.int32)  # 使用int32构建图
g32.idtype
g64_2 = g32.long()  # 转换成int64
g64_2.idtype
g32_2 = g64.int()  # 转换成int32
g32_2.idtype

相关API：dgl.graph()、 dgl.DGLGraph.nodes()、 dgl.DGLGraph.edges()、 dgl.to_bidirected()、 dgl.DGLGraph.int()、 dgl.DGLGraph.long() 和 dgl.DGLGraph.idtype。

1.3 节点和边的特征

DGLGraph 对象的节点和边可具有多个用户定义的、可命名的特征，以储存图的节点和边的属性。 通过 ndata 和 edata 接口可访问这些特征。 例如，以下代码创建了2个节点特征（分别在第8、15行命名为 ‘x’ 、 ‘y’ ）和1个边特征（在第9行命名为 ‘x’ ）。

import dgl
import torch as th
g = dgl.graph(([0, 0, 1, 5], [1, 2, 2, 0])) # 6个节点，4条边
g
g.ndata['x'] = th.ones(g.num_nodes(), 3)               # 长度为3的节点特征
g.edata['x'] = th.ones(g.num_edges(), dtype=th.int32)  # 标量整型特征
g
# 不同名称的特征可以具有不同形状
g.ndata['y'] = th.randn(g.num_nodes(), 5)
g.ndata['x'][1]                  # 获取节点1的特征
g.edata['x'][th.tensor([0, 3])]  # 获取边0和3的特征

关于 ndata 和 edata 接口的重要说明：

仅允许使用数值类型（如单精度浮点型、双精度浮点型和整型）的特征。这些特征可以是标量、向量或多维张量。

每个节点特征具有唯一名称，每个边特征也具有唯一名称。节点和边的特征可以具有相同的名称（如上述示例代码中的 ‘x’ ）。

通过张量分配创建特征时，DGL会将特征赋给图中的每个节点和每条边。该张量的第一维必须与图中节点或边的数量一致。 不能将特征赋给图中节点或边的子集。

相同名称的特征必须具有相同的维度和数据类型。

特征张量使用”行优先”的原则，即每个行切片储存1个节点或1条边的特征（参考上述示例代码的第16和18行）。

对于加权图，用户可以将权重储存为一个边特征，如下。

# 边 0->1, 0->2, 0->3, 1->3
edges = th.tensor([0, 0, 0, 1]), th.tensor([1, 2, 3, 3])
weights = th.tensor([0.1, 0.6, 0.9, 0.7])  # 每条边的权重
g = dgl.graph(edges)
g.edata['w'] = weights  # 将其命名为 'w'

相关API： ndata、 edata。

1.4 从外部源创建图

可以从外部来源构造一个 DGLGraph 对象，包括：

从用于图和稀疏矩阵的外部Python库（NetworkX 和 SciPy）创建而来。

从磁盘加载图数据。

本节不涉及通过转换其他图来生成图的函数，相关概述请阅读API参考手册。

从外部库创建图

以下代码片段为从SciPy稀疏矩阵和NetworkX图创建DGL图的示例。

import dgl
import torch as th
import scipy.sparse as sp
spmat = sp.rand(100, 100, density=0.05) # 5%非零项
dgl.from_scipy(spmat)                   # 来自SciPy
Graph(num_nodes=100, num_edges=500,
      ndata_schemes={}
      edata_schemes={})

import networkx as nx
nx_g = nx.path_graph(5) # 一条链路0-1-2-3-4
dgl.from_networkx(nx_g) # 来自NetworkX
Graph(num_nodes=5, num_edges=8,
      ndata_schemes={}
      edata_schemes={})

注意，当使用 nx.path_graph(5) 进行创建时， DGLGraph 对象有8条边，而非4条。 这是由于 nx.path_graph(5) 构建了一个无向的NetworkX图 networkx.Graph ，而 DGLGraph 的边总是有向的。 所以当将无向的NetworkX图转换为 DGLGraph 对象时，DGL会在内部将1条无向边转换为2条有向边。 使用有向的NetworkX图 networkx.DiGraph 可避免该行为。

nxg = nx.DiGraph([(2, 1), (1, 2), (2, 3), (0, 0)])
dgl.from_networkx(nxg)
Graph(num_nodes=4, num_edges=4,
      ndata_schemes={}
      edata_schemes={})

Note

DGL在内部将SciPy矩阵和NetworkX图转换为张量来创建图。因此，这些构建方法并不适用于重视性能的场景。

相关API： dgl.from_scipy()、 dgl.from_networkx()。

从磁盘加载图

有多种文件格式可储存图，所以这里难以枚举所有选项。本节仅给出一些常见格式的一般情况。

逗号分隔值（CSV）

CSV是一种常见的格式，以表格格式储存节点、边及其特征：

nodes.csv
age, title

43, 1

23, 3

…

edges.csv
src, dst, weight

0, 1, 0.4

0, 3, 0.9

…

许多知名Python库(如Pandas)可以将该类型数据加载到python对象(如 numpy.ndarray)中， 进而使用这些对象来构建DGLGraph对象。如果后端框架也提供了从磁盘中保存或加载张量的工具(如 torch.save(), torch.load() )， 可以遵循相同的原理来构建图。

另见： 从成对的边 CSV 文件中加载 Karate Club Network 的教程。

JSON/GML 格式

如果对速度不太关注的话，读者可以使用NetworkX提供的工具来解析 各种数据格式， DGL可以间接地从这些来源创建图。

DGL 二进制格式

DGL提供了API以从磁盘中加载或向磁盘里保存二进制格式的图。除了图结构，API也能处理特征数据和图级别的标签数据。 DGL也支持直接从S3/HDFS中加载或向S3/HDFS保存图。参考手册提供了该用法的更多细节。

相关API： dgl.save_graphs()、 dgl.load_graphs()。

1.5 异构图

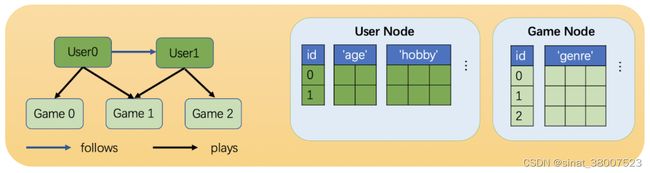
相比同构图，异构图里可以有不同类型的节点和边。这些不同类型的节点和边具有独立的ID空间和特征。 例如在下图中，”用户”和”游戏”节点的ID都是从0开始的，而且两种节点具有不同的特征。

一个异构图示例。该图具有两种类型的节点(“用户”和”游戏”)和两种类型的边(“关注”和”玩”)。

创建异构图

在DGL中，一个异构图由一系列子图构成，一个子图对应一种关系。每个关系由一个字符串三元组 定义 (源节点类型, 边类型, 目标节点类型) 。由于这里的关系定义消除了边类型的歧义，DGL称它们为规范边类型。

下面的代码是一个在DGL中创建异构图的示例。

import dgl
import torch as th

# 创建一个具有3种节点类型和3种边类型的异构图
graph_data = {
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
}
g = dgl.heterograph(graph_data)
g.ntypes
['disease', 'drug', 'gene']
g.etypes
['interacts', 'interacts', 'treats']
g.canonical_etypes
[('drug', 'interacts', 'drug'),
 ('drug', 'interacts', 'gene'),
 ('drug', 'treats', 'disease')]

注意，同构图和二分图只是一种特殊的异构图，它们只包括一种关系。

# 一个同构图
dgl.heterograph({('node_type', 'edge_type', 'node_type'): (u, v)})
# 一个二分图
dgl.heterograph({('source_type', 'edge_type', 'destination_type'): (u, v)})

与异构图相关联的 metagraph 就是图的模式。它指定节点集和节点之间的边的类型约束。 metagraph 中的一个节点 u 对应于相关异构图中的一个节点类型。 metagraph 中的边 (u,v) 表示在相关异构图中存在从 u 型节点到 v 型节点的边。

g
Graph(num_nodes={'disease': 3, 'drug': 3, 'gene': 4},
      num_edges={('drug', 'interacts', 'drug'): 2,
                 ('drug', 'interacts', 'gene'): 2,
                 ('drug', 'treats', 'disease'): 1},
      metagraph=[('drug', 'drug', 'interacts'),
                 ('drug', 'gene', 'interacts'),
                 ('drug', 'disease', 'treats')])
g.metagraph().edges()
OutMultiEdgeDataView([('drug', 'drug'), ('drug', 'gene'), ('drug', 'disease')])
相关API: dgl.heterograph()、 ntypes、 etypes、 canonical_etypes、 metagraph。

使用多种类型

当引入多种节点和边类型后，用户在调用DGLGraph API以获取特定类型的信息时，需要指定具体的节点和边类型。此外，不同类型的节点和边具有单独的ID。

# 获取图中所有节点的数量
g.num_nodes()
10
# 获取drug节点的数量
g.num_nodes('drug')
3
# 不同类型的节点有单独的ID。因此，没有指定节点类型就没有明确的返回值。
g.nodes()
DGLError: Node type name must be specified if there are more than one node types.
g.nodes('drug')
tensor([0, 1, 2])

为了设置/获取特定节点和边类型的特征，DGL提供了两种新类型的语法：

g.nodes[‘node_type’].data[‘feat_name’] 和 g.edges[‘edge_type’].data[‘feat_name’] 。

# 设置/获取"drug"类型的节点的"hv"特征
g.nodes['drug'].data['hv'] = th.ones(3, 1)
g.nodes['drug'].data['hv']
tensor([[1.],
        [1.],
        [1.]])
# 设置/获取"treats"类型的边的"he"特征
g.edges['treats'].data['he'] = th.zeros(1, 1)
g.edges['treats'].data['he']
tensor([[0.]])

如果图里只有一种节点或边类型，则不需要指定节点或边的类型。

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'is similar', 'drug'): (th.tensor([0, 1]), th.tensor([2, 3]))
})
g.nodes()
tensor([0, 1, 2, 3])
# 设置/获取单一类型的节点或边特征，不必使用新的语法
g.ndata['hv'] = th.ones(4, 1)

Note

当边类型唯一地确定了源节点和目标节点的类型时，用户可以只使用一个字符串而不是字符串三元组来指定边类型。例如， 对于具有两个关系
(‘user’, ‘plays’, ‘game’) 和 (‘user’, ‘likes’, ‘game’) 的异构图， 只使用
‘plays’ 或 ‘like’ 来指代这两个关系是可以的。

从磁盘加载异构图

逗号分隔值（CSV）

一种存储异构图的常见方法是在不同的CSV文件中存储不同类型的节点和边。下面是一个例子。

# 数据文件夹
data/
|-- drug.csv        # drug节点
|-- gene.csv        # gene节点
|-- disease.csv     # disease节点
|-- drug-interact-drug.csv  # drug-drug相互作用边
|-- drug-interact-gene.csv  # drug-gene相互作用边
|-- drug-treat-disease.csv  # drug-disease治疗边

与同构图的情况类似，用户可以使用像Pandas这样的包先将CSV文件解析为numpy数组或框架张量，再构建一个关系字典，并用它构造一个异构图。 这种方法也适用于其他流行的文件格式，比如GML或JSON。

DGL二进制格式

DGL提供了 dgl.save_graphs() 和 dgl.load_graphs() 函数，分别用于以二进制格式保存异构图和加载它们。

边类型子图

用户可以通过指定要保留的关系来创建异构图的子图，相关的特征也会被拷贝。

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
})
g.nodes['drug'].data['hv'] = th.ones(3, 1)

# 保留关系 ('drug', 'interacts', 'drug') 和 ('drug', 'treats', 'disease') 。
# 'drug' 和 'disease' 类型的节点也会被保留
eg = dgl.edge_type_subgraph(g, [('drug', 'interacts', 'drug'),
                                ('drug', 'treats', 'disease')])
eg
Graph(num_nodes={'disease': 3, 'drug': 3},
      num_edges={('drug', 'interacts', 'drug'): 2, ('drug', 'treats', 'disease'): 1},
      metagraph=[('drug', 'drug', 'interacts'), ('drug', 'disease', 'treats')])
# 相关的特征也会被拷贝
eg.nodes['drug'].data['hv']
tensor([[1.],
        [1.],
        [1.]])

将异构图转化为同构图

异构图为管理不同类型的节点和边及其相关特征提供了一个清晰的接口。这在以下情况下尤其有用:

不同类型的节点和边的特征具有不同的数据类型或大小。

用户希望对不同类型的节点和边应用不同的操作。

如果上述情况不适用，并且用户不希望在建模中区分节点和边的类型，则DGL允许使用 dgl.DGLGraph.to_homogeneous() API将异构图转换为同构图。 具体行为如下:

用从0开始的连续整数重新标记所有类型的节点和边。

对所有的节点和边合并用户指定的特征。

```bash
g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))})
g.nodes['drug'].data['hv'] = th.zeros(3, 1)
g.nodes['disease'].data['hv'] = th.ones(3, 1)
g.edges['interacts'].data['he'] = th.zeros(2, 1)
g.edges['treats'].data['he'] = th.zeros(1, 2)

# 默认情况下不进行特征合并
hg = dgl.to_homogeneous(g)
'hv' in hg.ndata
False

# 拷贝边的特征
# 对于要拷贝的特征，DGL假定不同类型的节点或边的需要合并的特征具有相同的大小和数据类型
hg = dgl.to_homogeneous(g, edata=['he'])
DGLError: Cannot concatenate column ‘he’ with shape Scheme(shape=(2,), dtype=torch.float32) and shape Scheme(shape=(1,), dtype=torch.float32)

# 拷贝节点特征
hg = dgl.to_homogeneous(g, ndata=['hv'])
hg.ndata['hv']
tensor([[1.],
        [1.],
        [1.],
        [0.],
        [0.],
        [0.]])

原始的节点或边的类型和对应的ID被存储在 ndata 和 edata 中。

# 异构图中节点类型的顺序
g.ntypes
['disease', 'drug']
# 原始节点类型
hg.ndata[dgl.NTYPE]
tensor([0, 0, 0, 1, 1, 1])
# 原始的特定类型节点ID
hg.ndata[dgl.NID]
tensor([0, 1, 2, 0, 1, 2])

# 异构图中边类型的顺序
g.etypes
['interacts', 'treats']
# 原始边类型
hg.edata[dgl.ETYPE]
tensor([0, 0, 1])
# 原始的特定类型边ID
hg.edata[dgl.EID]
tensor([0, 1, 0])

出于建模的目的，用户可能需要将一些关系合并，并对它们应用相同的操作。为了实现这一目的，可以先抽取异构图的边类型子图，然后将该子图转换为同构图。

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
})
sub_g = dgl.edge_type_subgraph(g, [('drug', 'interacts', 'drug'),
                                   ('drug', 'interacts', 'gene')])
h_sub_g = dgl.to_homogeneous(sub_g)
h_sub_g
Graph(num_nodes=7, num_edges=4,
      ...)

第2章：消息传递范式

消息传递是实现GNN的一种通用框架和编程范式。它从聚合与更新的角度归纳总结了多种GNN模型的实现。

消息传递范式

假设节点 v 上的的特征为 xv∈Rd1，边 (u,v) 上的特征为 we∈Rd2。 消息传递范式 定义了以下逐节点和边上的计算：

边上计算: m(t+1)e=ϕ(x(t)v,x(t)u,w(t)e),(u,v,e)∈E.
点上计算: x(t+1)v=ψ(x(t)v,ρ({m(t+1)e:(u,v,e)∈E})).
在上面的等式中， ϕ 是定义在每条边上的消息函数，它通过将边上特征与其两端节点的特征相结合来生成消息。 聚合函数 ρ 会聚合节点接受到的消息。 更新函数 ψ 会结合聚合后的消息和节点本身的特征来更新节点的特征。

本章路线图

本章首先介绍了DGL的消息传递API。然后讲解了如何高效地在点和边上使用这些API。本章的最后一节解释了如何在异构图上实现消息传递。

2.1 内置函数和消息传递API

2.2 编写高效的消息传递代码

2.3 在图的一部分上进行消息传递

2.4 在异构图上进行消息传递

2.1 内置函数和消息传递API

在DGL中，消息函数 接受一个参数 edges，这是一个 EdgeBatch 的实例， 在消息传递时，它被DGL在内部生成以表示一批边。 edges 有 src、 dst 和 data 共3个成员属性， 分别用于访问源节点、目标节点和边的特征。

聚合函数 接受一个参数 nodes，这是一个 NodeBatch 的实例， 在消息传递时，它被DGL在内部生成以表示一批节点。 nodes 的成员属性 mailbox 可以用来访问节点收到的消息。 一些最常见的聚合操作包括 sum、max、min 等。

更新函数 接受一个如上所述的参数 nodes。此函数对 聚合函数 的聚合结果进行操作， 通常在消息传递的最后一步将其与节点的特征相结合，并将输出作为节点的新特征。

DGL在命名空间 dgl.function 中实现了常用的消息函数和聚合函数作为 内置函数。 一般来说，DGL建议 尽可能 使用内置函数，因为它们经过了大量优化，并且可以自动处理维度广播。

如果用户的消息传递函数无法用内置函数实现，则可以实现自己的消息或聚合函数(也称为 用户定义函数 )。

内置消息函数可以是一元函数或二元函数。对于一元函数，DGL支持 copy 函数。对于二元函数， DGL现在支持 add、 sub、 mul、 div、 dot 函数。消息的内置函数的命名约定是 u 表示 源 节点， v 表示 目标 节点，e 表示 边。这些函数的参数是字符串，指示相应节点和边的输入和输出特征字段名。 关于内置函数的列表，请参见 DGL Built-in Function。例如，要对源节点的 hu 特征和目标节点的 hv 特征求和， 然后将结果保存在边的 he 特征上，用户可以使用内置函数 dgl.function.u_add_v(‘hu’, ‘hv’, ‘he’)。 而以下用户定义消息函数与此内置函数等价。

def message_func(edges):
     return {'he': edges.src['hu'] + edges.dst['hv']}

DGL支持内置的聚合函数 sum、 max、 min 和 mean 操作。 聚合函数通常有两个参数，它们的类型都是字符串。一个用于指定 mailbox 中的字段名，一个用于指示目标节点特征的字段名， 例如， dgl.function.sum(‘m’, ‘h’) 等价于如下所示的对接收到消息求和的用户定义函数：

import torch
def reduce_func(nodes):
     return {'h': torch.sum(nodes.mailbox['m'], dim=1)}

关于用户定义函数的进阶用法，参见 User-defined Functions。

在DGL中，也可以在不涉及消息传递的情况下，通过 apply_edges() 单独调用逐边计算。 apply_edges() 的参数是一个消息函数。并且在默认情况下，这个接口将更新所有的边。例如：

import dgl.function as fn
graph.apply_edges(fn.u_add_v('el', 'er', 'e'))

对于消息传递， update_all() 是一个高级API。它在单个API调用里合并了消息生成、 消息聚合和节点特征更新，这为从整体上进行系统优化提供了空间。

update_all() 的参数是一个消息函数、一个聚合函数和一个更新函数。 更新函数是一个可选择的参数，用户也可以不使用它，而是在 update_all 执行完后直接对节点特征进行操作。 由于更新函数通常可以用纯张量操作实现，所以DGL不推荐在 update_all 中指定更新函数。例如：

def update_all_example(graph):
    # 在graph.ndata['ft']中存储结果
    graph.update_all(fn.u_mul_e('ft', 'a', 'm'),
                     fn.sum('m', 'ft'))
    # 在update_all外调用更新函数
    final_ft = graph.ndata['ft'] * 2
    return final_ft

此调用通过将源节点特征 ft 与边特征 a 相乘生成消息 m， 然后对所有消息求和来更新节点特征 ft，再将 ft 乘以2得到最终结果 final_ft。

调用后，中间消息 m 将被清除。上述函数的数学公式为：
${final\_ft}_i=2\ast {\sum }_{j\in \mathcal{N}(i)}({ft}_j\ast a_{ij})$

2.2 编写高效的消息传递代码

DGL优化了消息传递的内存消耗和计算速度。利用这些优化的一个常见实践是通过基于内置函数的 update_all() 来开发消息传递功能。

除此之外，考虑到某些图边的数量远远大于节点的数量，DGL建议避免不必要的从点到边的内存拷贝。对于某些情况，比如 GATConv，计算必须在边上保存消息， 那么用户就需要调用基于内置函数的 apply_edges()。有时边上的消息可能是高维的，这会非常消耗内存。 DGL建议用户尽量减少边的特征维数。

下面是一个如何通过对节点特征降维来减少消息维度的示例。该做法执行以下操作：拼接 源 节点和 目标 节点特征， 然后应用一个线性层，即 W×(u||v)。 源 节点和 目标 节点特征维数较高，而线性层输出维数较低。 一个直截了当的实现方式如下：

import torch
import torch.nn as nn

linear = nn.Parameter(torch.FloatTensor(size=(node_feat_dim * 2, out_dim)))
def concat_message_function(edges):
     return {'cat_feat': torch.cat([edges.src['feat'], edges.dst['feat']], dim=1)}
g.apply_edges(concat_message_function)
g.edata['out'] = g.edata['cat_feat'] @ linear

建议的实现是将线性操作分成两部分，一个应用于 源 节点特征，另一个应用于 目标 节点特征。 在最后一个阶段，在边上将以上两部分线性操作的结果相加，即执行 Wl×u+Wr×v， 因为 $W\times (u||v)=W_l\times u+W_r\times v$，其中 Wl 和 Wr 分别是矩阵 W 的左半部分和右半部分：

import dgl.function as fn

linear_src = nn.Parameter(torch.FloatTensor(size=(node_feat_dim, out_dim)))
linear_dst = nn.Parameter(torch.FloatTensor(size=(node_feat_dim, out_dim)))
out_src = g.ndata['feat'] @ linear_src
out_dst = g.ndata['feat'] @ linear_dst
g.srcdata.update({'out_src': out_src})
g.dstdata.update({'out_dst': out_dst})
g.apply_edges(fn.u_add_v('out_src', 'out_dst', 'out'))

以上两个实现在数学上是等价的。后一种方法效率高得多，因为不需要在边上保存feat_src和feat_dst， 从内存角度来说是高效的。另外，加法可以通过DGL的内置函数 u_add_v 进行优化，从而进一步加快计算速度并节省内存占用。

2.3 在图的一部分上进行消息传递

如果用户只想更新图中的部分节点，可以先通过想要囊括的节点编号创建一个子图， 然后在子图上调用 update_all() 方法。例如：

nid = [0, 2, 3, 6, 7, 9]
sg = g.subgraph(nid)
sg.update_all(message_func, reduce_func, apply_node_func)

这是小批量训练中的常见用法。更多详细用法请参考用户指南 第6章：在大图上的随机（批次）训练。

2.4 在异构图上进行消息传递

异构图（参考用户指南 1.5 异构图 ）是包含不同类型的节点和边的图。 不同类型的节点和边常常具有不同类型的属性。这些属性旨在刻画每一种节点和边的特征。在使用图神经网络时，根据其复杂性， 可能需要使用不同维度的表示来对不同类型的节点和边进行建模。

异构图上的消息传递可以分为两个部分：

对每个关系计算和聚合消息。

对每个结点聚合来自不同关系的消息。

在DGL中，对异构图进行消息传递的接口是 multi_update_all()。 multi_update_all() 接受一个字典。这个字典的每一个键值对里，键是一种关系， 值是这种关系对应 update_all() 的参数。 multi_update_all() 还接受一个字符串来表示跨类型整合函数，来指定整合不同关系聚合结果的方式。 这个整合方式可以是 sum、 min、 max、 mean 和 stack 中的一个。以下是一个例子：

import dgl.function as fn

for c_etype in G.canonical_etypes:
    srctype, etype, dsttype = c_etype
    Wh = self.weight[etype](feat_dict[srctype])
    # 把它存在图中用来做消息传递
    G.nodes[srctype].data['Wh_%s' % etype] = Wh
    # 指定每个关系的消息传递函数：(message_func, reduce_func).
    # 注意结果保存在同一个目标特征“h”，说明聚合是逐类进行的。
    funcs[etype] = (fn.copy_u('Wh_%s' % etype, 'm'), fn.mean('m', 'h'))
# 将每个类型消息聚合的结果相加。
G.multi_update_all(funcs, 'sum')
# 返回更新过的节点特征字典
return {ntype : G.nodes[ntype].data['h'] for ntype in G.ntypes}

第3章：构建图神经网络（GNN）模块

DGL NN模块是用户构建GNN模型的基本模块。根据DGL所使用的后端深度神经网络框架， DGL NN模块的父类取决于后端所使用的深度神经网络框架。对于PyTorch后端， 它应该继承 PyTorch的NN模块；对于MXNet后端，它应该继承 MXNet Gluon的NN块； 对于TensorFlow后端，它应该继承 Tensorflow的Keras层。 在DGL NN模块中，构造函数中的参数注册和前向传播函数中使用的张量操作与后端框架一样。这种方式使得DGL的代码可以无缝嵌入到后端框架的代码中。 DGL和这些深度神经网络框架的主要差异是其独有的消息传递操作。

DGL已经集成了很多常用的 apinn-pytorch-conv、 apinn-pytorch-dense-conv、 apinn-pytorch-pooling 和 apinn-pytorch-util。欢迎给DGL贡献更多的模块！

本章将使用PyTorch作为后端，用 SAGEConv 作为例子来介绍如何构建用户自己的DGL NN模块。

本章路线图

3.1 DGL NN模块的构造函数

3.2 编写DGL NN模块的forward函数

3.3 异构图上的GraphConv模块

3.1 DGL NN模块的构造函数

构造函数完成以下几个任务：

设置选项。

注册可学习的参数或者子模块。

初始化参数。

import torch.nn as nn

from dgl.utils import expand_as_pair

class SAGEConv(nn.Module):
    def __init__(self,
                 in_feats,
                 out_feats,
                 aggregator_type,
                 bias=True,
                 norm=None,
                 activation=None):
        super(SAGEConv, self).__init__()

        self._in_src_feats, self._in_dst_feats = expand_as_pair(in_feats)
        self._out_feats = out_feats
        self._aggre_type = aggregator_type
        self.norm = norm
        self.activation = activation

在构造函数中，用户首先需要设置数据的维度。对于一般的PyTorch模块，维度通常包括输入的维度、输出的维度和隐层的维度。 对于图神经网络，输入维度可被分为源节点特征维度和目标节点特征维度。

除了数据维度，图神经网络的一个典型选项是聚合类型(self._aggre_type)。对于特定目标节点，聚合类型决定了如何聚合不同边上的信息。 常用的聚合类型包括 mean、 sum、 max 和 min。一些模块可能会使用更加复杂的聚合函数，比如 lstm。

上面代码里的 norm 是用于特征归一化的可调用函数。在SAGEConv论文里，归一化可以是L2归一化: hv=hv/∥hv∥2。

# 聚合类型：mean、pool、lstm、gcn
if aggregator_type not in ['mean', 'pool', 'lstm', 'gcn']:
    raise KeyError('Aggregator type {} not supported.'.format(aggregator_type))
if aggregator_type == 'pool':
    self.fc_pool = nn.Linear(self._in_src_feats, self._in_src_feats)
if aggregator_type == 'lstm':
    self.lstm = nn.LSTM(self._in_src_feats, self._in_src_feats, batch_first=True)
if aggregator_type in ['mean', 'pool', 'lstm']:
    self.fc_self = nn.Linear(self._in_dst_feats, out_feats, bias=bias)
self.fc_neigh = nn.Linear(self._in_src_feats, out_feats, bias=bias)
self.reset_parameters()

注册参数和子模块。在SAGEConv中，子模块根据聚合类型而有所不同。这些模块是纯PyTorch NN模块，例如 nn.Linear、 nn.LSTM 等。 构造函数的最后调用了 reset_parameters() 进行权重初始化。

def reset_parameters(self):
    """重新初始化可学习的参数"""
    gain = nn.init.calculate_gain('relu')
    if self._aggre_type == 'pool':
        nn.init.xavier_uniform_(self.fc_pool.weight, gain=gain)
    if self._aggre_type == 'lstm':
        self.lstm.reset_parameters()
    if self._aggre_type != 'gcn':
        nn.init.xavier_uniform_(self.fc_self.weight, gain=gain)
    nn.init.xavier_uniform_(self.fc_neigh.weight, gain=gain)

3.2 编写DGL NN模块的forward函数

在NN模块中， forward() 函数执行了实际的消息传递和计算。与通常以张量为参数的PyTorch NN模块相比， DGL NN模块额外增加了1个参数 dgl.DGLGraph。forward() 函数的内容一般可以分为3项操作：

检测输入图对象是否符合规范。

消息传递和聚合。

聚合后，更新特征作为输出。

下文展示了SAGEConv示例中的 forward() 函数。

输入图对象的规范检测

def forward(self, graph, feat):
    with graph.local_scope():
        # 指定图类型，然后根据图类型扩展输入特征
        feat_src, feat_dst = expand_as_pair(feat, graph)

forward() 函数需要处理输入的许多极端情况，这些情况可能导致计算和消息传递中的值无效。 比如在 GraphConv 等conv模块中，DGL会检查输入图中是否有入度为0的节点。 当1个节点入度为0时， mailbox 将为空，并且聚合函数的输出值全为0， 这可能会导致模型性能不佳。但是，在 SAGEConv 模块中，被聚合的特征将会与节点的初始特征拼接起来， forward() 函数的输出不会全为0。在这种情况下，无需进行此类检验。

DGL NN模块可在不同类型的图输入中重复使用，包括：同构图、异构图（1.5 异构图）和子图块（第6章：在大图上的随机（批次）训练）。

SAGEConv的数学公式如下：

$h_{\mathcal{N}(dst)}^{(l+1)}=\mathrm{aggregate}\left(\{h_{src}^l,\forall src\in \mathcal{N}(dst)\}\right)$
$h_{dst}^{(l+1)}=\sigma \left(W\cdot \mathrm{concat}(h_{dst}^l,h_{\mathcal{N}(dst)}^{l+1})+b\right)$
$h_{dst}^{(l+1)}=\mathrm{norm}(h_{dst}^{l+1})$
源节点特征 feat_src 和目标节点特征 feat_dst 需要根据图类型被指定。 用于指定图类型并将 feat 扩展为 feat_src 和 feat_dst 的函数是 expand_as_pair()。 该函数的细节如下所示。

def expand_as_pair(input_, g=None):
    if isinstance(input_, tuple):
        # 二分图的情况
        return input_
    elif g is not None and g.is_block:
        # 子图块的情况
        if isinstance(input_, Mapping):
            input_dst = {
                k: F.narrow_row(v, 0, g.number_of_dst_nodes(k))
                for k, v in input_.items()}
        else:
            input_dst = F.narrow_row(input_, 0, g.number_of_dst_nodes())
        return input_, input_dst
    else:
        # 同构图的情况
        return input_, input_

对于同构图上的全图训练，源节点和目标节点相同，它们都是图中的所有节点。

在异构图的情况下，图可以分为几个二分图，每种关系对应一个。关系表示为 (src_type, edge_type, dst_dtype)。 当输入特征 feat 是1个元组时，图将会被视为二分图。元组中的第1个元素为源节点特征，第2个元素为目标节点特征。

在小批次训练中，计算应用于给定的一堆目标节点所采样的子图。子图在DGL中称为区块(block)。 在区块创建的阶段，dst nodes 位于节点列表的最前面。通过索引 [0:g.number_of_dst_nodes()] 可以找到 feat_dst。

确定 feat_src 和 feat_dst 之后，以上3种图类型的计算方法是相同的。

消息传递和聚合

import dgl.function as fn
import torch.nn.functional as F
from dgl.utils import check_eq_shape

if self._aggre_type == 'mean':
    graph.srcdata['h'] = feat_src
    graph.update_all(fn.copy_u('h', 'm'), fn.mean('m', 'neigh'))
    h_neigh = graph.dstdata['neigh']
elif self._aggre_type == 'gcn':
    check_eq_shape(feat)
    graph.srcdata['h'] = feat_src
    graph.dstdata['h'] = feat_dst
    graph.update_all(fn.copy_u('h', 'm'), fn.sum('m', 'neigh'))
    # 除以入度
    degs = graph.in_degrees().to(feat_dst)
    h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'pool':
    graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
    graph.update_all(fn.copy_u('h', 'm'), fn.max('m', 'neigh'))
    h_neigh = graph.dstdata['neigh']
else:
    raise KeyError('Aggregator type {} not recognized.'.format(self._aggre_type))

# GraphSAGE中gcn聚合不需要fc_self
if self._aggre_type == 'gcn':
    rst = self.fc_neigh(h_neigh)
else:
    rst = self.fc_self(h_self) + self.fc_neigh(h_neigh)

上面的代码执行了消息传递和聚合的计算。这部分代码会因模块而异。请注意，代码中的所有消息传递均使用 update_all() API和 DGL内置的消息/聚合函数来实现，以充分利用 2.2 编写高效的消息传递代码 里所介绍的性能优化。

聚合后，更新特征作为输出

# 激活函数
if self.activation is not None:
    rst = self.activation(rst)
# 归一化
if self.norm is not None:
    rst = self.norm(rst)
return rst

forward() 函数的最后一部分是在完成消息聚合后更新节点的特征。 常见的更新操作是根据构造函数中设置的选项来应用激活函数和进行归一化。

3.3 异构图上的GraphConv模块

DGL提供了 HeteroGraphConv，用于定义异构图上GNN模块。 实现逻辑与消息传递级别的API multi_update_all() 相同，它包括：

每个关系上的DGL NN模块。

聚合来自不同关系上的结果。

其数学定义为：
$h_{dst}^{(l+1)}=\underset{r\in \mathcal{R},r_{dst}=dst}{\mathrm{AGG}}(f_r(g_r,h_{r_{src}}^l,h_{r_{dst}}^l))$

其中 fr 是对应每个关系 r 的NN模块，AGG 是聚合函数。

HeteroGraphConv的实现逻辑

import torch.nn as nn

class HeteroGraphConv(nn.Module):
    def __init__(self, mods, aggregate='sum'):
        super(HeteroGraphConv, self).__init__()
        self.mods = nn.ModuleDict(mods)
        if isinstance(aggregate, str):
            # 获取聚合函数的内部函数
            self.agg_fn = get_aggregate_fn(aggregate)
        else:
            self.agg_fn = aggregate

异构图的卷积操作接受一个字典类型参数 mods。这个字典的键为关系名，值为作用在该关系上NN模块对象。参数 aggregate 则指定了如何聚合来自不同关系的结果。

def forward(self, g, inputs, mod_args=None, mod_kwargs=None):
    if mod_args is None:
        mod_args = {}
    if mod_kwargs is None:
        mod_kwargs = {}
    outputs = {nty : [] for nty in g.dsttypes}

除了输入图和输入张量，forward() 函数还使用2个额外的字典参数 mod_args 和 mod_kwargs。 这2个字典与 self.mods 具有相同的键，值则为对应NN模块的自定义参数。

forward() 函数的输出结果也是一个字典类型的对象。其键为 nty，其值为每个目标节点类型 nty 的输出张量的列表， 表示来自不同关系的计算结果。HeteroGraphConv 会对这个列表进一步聚合，并将结果返回给用户。

if g.is_block:
    src_inputs = inputs
    dst_inputs = {k: v[:g.number_of_dst_nodes(k)] for k, v in inputs.items()}
else:
    src_inputs = dst_inputs = inputs

for stype, etype, dtype in g.canonical_etypes:
    rel_graph = g[stype, etype, dtype]
    if rel_graph.num_edges() == 0:
        continue
    if stype not in src_inputs or dtype not in dst_inputs:
        continue
    dstdata = self.mods[etype](
        rel_graph,
        (src_inputs[stype], dst_inputs[dtype]),
        *mod_args.get(etype, ()),
        **mod_kwargs.get(etype, {}))
    outputs[dtype].append(dstdata)

输入 g 可以是异构图或来自异构图的子图区块。和普通的NN模块一样，forward() 函数需要分别处理不同的输入图类型。

上述代码中的for循环为处理异构图计算的主要逻辑。首先我们遍历图中所有的关系(通过调用 canonical_etypes)。 通过关系名，我们可以使用g[ stype, etype, dtype ]的语法将只包含该关系的子图( rel_graph )抽取出来。 对于二分图，输入特征将被组织为元组 (src_inputs[stype], dst_inputs[dtype])。 接着调用用户预先注册在该关系上的NN模块，并将结果保存在outputs字典中。

rsts = {}
for nty, alist in outputs.items():
    if len(alist) != 0:
        rsts[nty] = self.agg_fn(alist, nty)

最后，HeteroGraphConv 会调用用户注册的 self.agg_fn 函数聚合来自多个关系的结果。 读者可以在API文档中找到 :class:~dgl.nn.pytorch.HeteroGraphConv 的示例。

第4章：图数据处理管道

DGL在 dgl.data 里实现了很多常用的图数据集。它们遵循了由 dgl.data.DGLDataset 类定义的标准的数据处理管道。 DGL推荐用户将图数据处理为 dgl.data.DGLDataset 的子类。该类为导入、处理和保存图数据提供了简单而干净的解决方案。

本章路线图

本章介绍了如何为用户自己的图数据创建一个DGL数据集。以下内容说明了管道的工作方式，并展示了如何实现管道的每个组件。

4.1 DGLDataset类

4.2 下载原始数据（可选）

4.3 处理数据

4.4 保存和加载数据

4.5 使用ogb包导入OGB数据集

第5章：训练图神经网络

概述

本章通过使用 第2章：消息传递范式 中介绍的消息传递方法和 第3章：构建图神经网络（GNN）模块 中介绍的图神经网络模块， 讲解了如何对小规模的图数据进行节点分类、边分类、链接预测和整图分类的图神经网络的训练。

本章假设用户的图以及所有的节点和边特征都能存进GPU。对于无法全部载入的情况，请参考用户指南的 第6章：在大图上的随机（批次）训练。

后续章节的内容均假设用户已经准备好了图和节点/边的特征数据。如果用户希望使用DGL提供的数据集或其他兼容 DGLDataset 的数据(如 第4章：图数据处理管道 所述)， 可以使用类似以下代码的方法获取单个图数据集的图数据。

import dgl

dataset = dgl.data.CiteseerGraphDataset()
graph = dataset[0]

注意: 本章代码使用PyTorch作为DGL的后端框架。

异构图训练的样例数据

有时用户会想在异构图上进行图神经网络的训练。本章会以下面代码所创建的一个异构图为例，来演示如何进行节点分类、边分类和链接预测的训练。

这个 hetero_graph 异构图有以下这些边的类型：

• (‘user’, ‘follow’, ‘user’)

• (‘user’, ‘followed-by’, ‘user’)

• (‘user’, ‘click’, ‘item’)

• (‘item’, ‘clicked-by’, ‘user’)

• (‘user’, ‘dislike’, ‘item’)

• (‘item’, ‘disliked-by’, ‘user’)

import numpy as np
import torch

n_users = 1000
n_items = 500
n_follows = 3000
n_clicks = 5000
n_dislikes = 500
n_hetero_features = 10
n_user_classes = 5
n_max_clicks = 10

follow_src = np.random.randint(0, n_users, n_follows)
follow_dst = np.random.randint(0, n_users, n_follows)
click_src = np.random.randint(0, n_users, n_clicks)
click_dst = np.random.randint(0, n_items, n_clicks)
dislike_src = np.random.randint(0, n_users, n_dislikes)
dislike_dst = np.random.randint(0, n_items, n_dislikes)

hetero_graph = dgl.heterograph({
    ('user', 'follow', 'user'): (follow_src, follow_dst),
    ('user', 'followed-by', 'user'): (follow_dst, follow_src),
    ('user', 'click', 'item'): (click_src, click_dst),
    ('item', 'clicked-by', 'user'): (click_dst, click_src),
    ('user', 'dislike', 'item'): (dislike_src, dislike_dst),
    ('item', 'disliked-by', 'user'): (dislike_dst, dislike_src)})

hetero_graph.nodes['user'].data['feature'] = torch.randn(n_users, n_hetero_features)
hetero_graph.nodes['item'].data['feature'] = torch.randn(n_items, n_hetero_features)
hetero_graph.nodes['user'].data['label'] = torch.randint(0, n_user_classes, (n_users,))
hetero_graph.edges['click'].data['label'] = torch.randint(1, n_max_clicks, (n_clicks,)).float()
# 在user类型的节点和click类型的边上随机生成训练集的掩码
hetero_graph.nodes['user'].data['train_mask'] = torch.zeros(n_users, dtype=torch.bool).bernoulli(0.6)
hetero_graph.edges['click'].data['train_mask'] = torch.zeros(n_clicks, dtype=torch.bool).bernoulli(0.6)

本章路线图

本章共有四节，每节对应一种图学习任务。

5.1 节点分类/回归

5.2 边分类/回归

5.3 链接预测

5.4 整图分类

guide_cn-training-graph-eweight

5.1 节点分类/回归

对于图神经网络来说，最常见和被广泛使用的任务之一就是节点分类。 图数据中的训练、验证和测试集中的每个节点都具有从一组预定义的类别中分配的一个类别，即正确的标注。 节点回归任务也类似，训练、验证和测试集中的每个节点都被标注了一个正确的数字。

概述

为了对节点进行分类，图神经网络执行了 第2章：消息传递范式 中介绍的消息传递机制，利用节点自身的特征和其邻节点及边的特征来计算节点的隐藏表示。 消息传递可以重复多轮，以利用更大范围的邻居信息。

编写神经网络模型

DGL提供了一些内置的图卷积模块，可以完成一轮消息传递计算。 本章中选择 dgl.nn.pytorch.SAGEConv 作为演示的样例代码(针对MXNet和PyTorch后端也有对应的模块)， 它是GraphSAGE模型中使用的图卷积模块。

对于图上的深度学习模型，通常需要一个多层的图神经网络，并在这个网络中要进行多轮的信息传递。 可以通过堆叠图卷积模块来实现这种网络架构，具体如下所示。

# 构建一个2层的GNN模型
import dgl.nn as dglnn
import torch.nn as nn
import torch.nn.functional as F
class SAGE(nn.Module):
    def __init__(self, in_feats, hid_feats, out_feats):
        super().__init__()
        # 实例化SAGEConve，in_feats是输入特征的维度，out_feats是输出特征的维度，aggregator_type是聚合函数的类型
        self.conv1 = dglnn.SAGEConv(
            in_feats=in_feats, out_feats=hid_feats, aggregator_type='mean')
        self.conv2 = dglnn.SAGEConv(
            in_feats=hid_feats, out_feats=out_feats, aggregator_type='mean')

    def forward(self, graph, inputs):
        # 输入是节点的特征
        h = self.conv1(graph, inputs)
        h = F.relu(h)
        h = self.conv2(graph, h)
        return h

请注意，这个模型不仅可以做节点分类，还可以为其他下游任务获取隐藏节点表示，如： 5.2 边分类/回归、 5.3 链接预测 和 5.4 整图分类。

关于DGL内置图卷积模块的完整列表，读者可以参考 apinn。

有关DGL神经网络模块如何工作，以及如何编写一个自定义的带有消息传递的GNN模块的更多细节，请参考 第3章：构建图神经网络（GNN）模块 中的例子。

模型的训练

全图(使用所有的节点和边的特征)上的训练只需要使用上面定义的模型进行前向传播计算，并通过在训练节点上比较预测和真实标签来计算损失，从而完成后向传播。

本节使用DGL内置的数据集 dgl.data.CiteseerGraphDataset 来展示模型的训练。 节点特征和标签存储在其图上，训练、验证和测试的分割也以布尔掩码的形式存储在图上。这与在 第4章：图数据处理管道 中的做法类似。

node_features = graph.ndata['feat']
node_labels = graph.ndata['label']
train_mask = graph.ndata['train_mask']
valid_mask = graph.ndata['val_mask']
test_mask = graph.ndata['test_mask']
n_features = node_features.shape[1]
n_labels = int(node_labels.max().item() + 1)

下面是通过使用准确性来评估模型的一个例子。

def evaluate(model, graph, features, labels, mask):
model.eval()
with torch.no_grad():
logits = model(graph, features)
logits = logits[mask]
labels = labels[mask]
_, indices = torch.max(logits, dim=1)
correct = torch.sum(indices == labels)
return correct.item() * 1.0 / len(labels)
用户可以按如下方式实现模型的训练。

model = SAGE(in_feats=n_features, hid_feats=100, out_feats=n_labels)
opt = torch.optim.Adam(model.parameters())

for epoch in range(10):
    model.train()
    # 使用所有节点(全图)进行前向传播计算
    logits = model(graph, node_features)
    # 计算损失值
    loss = F.cross_entropy(logits[train_mask], node_labels[train_mask])
    # 计算验证集的准确度
    acc = evaluate(model, graph, node_features, node_labels, valid_mask)
    # 进行反向传播计算
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

    # 如果需要的话，保存训练好的模型。本例中省略。

DGL的GraphSAGE样例 提供了一个端到端的同构图节点分类的例子。用户可以在 GraphSAGE 类中看到模型实现的细节。 这个模型具有可调节的层数、dropout概率，以及可定制的聚合函数和非线性函数。

异构图上的节点分类模型的训练

如果图是异构的，用户可能希望沿着所有边类型从邻居那里收集消息。 用户可以使用 dgl.nn.pytorch.HeteroGraphConv 模块(针对MXNet和PyTorch后端也有对应的模块)在所有边类型上执行消息传递， 并为每种边类型使用一种图卷积模块。

下面的代码定义了一个异构图卷积模块。模块首先对每种边类型进行单独的图卷积计算，然后将每种边类型上的消息聚合结果再相加， 并作为所有节点类型的最终结果。

# Define a Heterograph Conv model

class RGCN(nn.Module):
    def __init__(self, in_feats, hid_feats, out_feats, rel_names):
        super().__init__()
        # 实例化HeteroGraphConv，in_feats是输入特征的维度，out_feats是输出特征的维度，aggregate是聚合函数的类型
        self.conv1 = dglnn.HeteroGraphConv({
            rel: dglnn.GraphConv(in_feats, hid_feats)
            for rel in rel_names}, aggregate='sum')
        self.conv2 = dglnn.HeteroGraphConv({
            rel: dglnn.GraphConv(hid_feats, out_feats)
            for rel in rel_names}, aggregate='sum')

    def forward(self, graph, inputs):
        # 输入是节点的特征字典
        h = self.conv1(graph, inputs)
        h = {k: F.relu(v) for k, v in h.items()}
        h = self.conv2(graph, h)
        return h

dgl.nn.HeteroGraphConv 接收一个节点类型和节点特征张量的字典作为输入，并返回另一个节点类型和节点特征的字典。

本章的 异构图训练的样例数据 中已经有了 user 和 item 的特征，用户可用如下代码获取。

model = RGCN(n_hetero_features, 20, n_user_classes, hetero_graph.etypes)
user_feats = hetero_graph.nodes['user'].data['feature']
item_feats = hetero_graph.nodes['item'].data['feature']
labels = hetero_graph.nodes['user'].data['label']
train_mask = hetero_graph.nodes['user'].data['train_mask']

然后，用户可以简单地按如下形式进行前向传播计算：

node_features = {'user': user_feats, 'item': item_feats}
h_dict = model(hetero_graph, {'user': user_feats, 'item': item_feats})
h_user = h_dict['user']
h_item = h_dict['item']

异构图上模型的训练和同构图的模型训练是一样的，只是这里使用了一个包括节点表示的字典来计算预测值。 例如，如果只预测 user 节点的类别，用户可以从返回的字典中提取 user 的节点嵌入。

opt = torch.optim.Adam(model.parameters())

for epoch in range(5):
    model.train()
    # 使用所有节点的特征进行前向传播计算，并提取输出的user节点嵌入
    logits = model(hetero_graph, node_features)['user']
    # 计算损失值
    loss = F.cross_entropy(logits[train_mask], labels[train_mask])
    # 计算验证集的准确度。在本例中省略。
    # 进行反向传播计算
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

    # 如果需要的话，保存训练好的模型。本例中省略。

DGL提供了一个用于节点分类的RGCN的端到端的例子 RGCN 。用户可以在 RGCN模型实现文件 中查看异构图卷积 RelGraphConvLayer 的具体定义。

5.2 边分类/回归

有时用户希望预测图中边的属性值，这种情况下，用户需要构建一个边分类/回归的模型。

以下代码生成了一个随机图用于演示边分类/回归。

src = np.random.randint(0, 100, 500)
dst = np.random.randint(0, 100, 500)
# 同时建立反向边
edge_pred_graph = dgl.graph((np.concatenate([src, dst]), np.concatenate([dst, src])))
# 建立点和边特征，以及边的标签
edge_pred_graph.ndata['feature'] = torch.randn(100, 10)
edge_pred_graph.edata['feature'] = torch.randn(1000, 10)
edge_pred_graph.edata['label'] = torch.randn(1000)
# 进行训练、验证和测试集划分
edge_pred_graph.edata['train_mask'] = torch.zeros(1000, dtype=torch.bool).bernoulli(0.6)

概述

上一节介绍了如何使用多层GNN进行节点分类。同样的方法也可以被用于计算任何节点的隐藏表示。 并从边的两个端点的表示，通过计算得出对边属性的预测。

对一条边计算预测值最常见的情况是将预测表示为一个函数，函数的输入为两个端点的表示， 输入还可以包括边自身的特征。

与节点分类在模型实现上的差别

如果用户使用上一节中的模型计算了节点的表示，那么用户只需要再编写一个用 apply_edges() 方法计算边预测的组件即可进行边分类/回归任务。

例如，对于边回归任务，如果用户想为每条边计算一个分数，可按下面的代码对每一条边计算它的两端节点隐藏表示的点积来作为分数。

import dgl.function as fn
class DotProductPredictor(nn.Module):
    def forward(self, graph, h):
        # h是从5.1节的GNN模型中计算出的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h
            graph.apply_edges(fn.u_dot_v('h', 'h', 'score'))
            return graph.edata['score']

用户也可以使用MLP(多层感知机)对每条边生成一个向量表示(例如，作为一个未经过归一化的类别的分布)， 并在下游任务中使用。

class MLPPredictor(nn.Module):
    def __init__(self, in_features, out_classes):
        super().__init__()
        self.W = nn.Linear(in_features * 2, out_classes)

    def apply_edges(self, edges):
        h_u = edges.src['h']
        h_v = edges.dst['h']
        score = self.W(torch.cat([h_u, h_v], 1))
        return {'score': score}

    def forward(self, graph, h):
        # h是从5.1节的GNN模型中计算出的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h
            graph.apply_edges(self.apply_edges)
            return graph.edata['score']

模型的训练

给定计算节点和边上表示的模型后，用户可以轻松地编写在所有边上进行预测的全图训练代码。

以下代码用了 第2章：消息传递范式 中定义的 SAGE 作为节点表示计算模型以及前一小节中定义的 DotPredictor 作为边预测模型。

class Model(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        super().__init__()
        self.sage = SAGE(in_features, hidden_features, out_features)
        self.pred = DotProductPredictor()
    def forward(self, g, x):
        h = self.sage(g, x)
        return self.pred(g, h)

在训练模型时可以使用布尔掩码区分训练、验证和测试数据集。该例子里省略了训练早停和模型保存部分的代码。

node_features = edge_pred_graph.ndata['feature']
edge_label = edge_pred_graph.edata['label']
train_mask = edge_pred_graph.edata['train_mask']
model = Model(10, 20, 5)
opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
    pred = model(edge_pred_graph, node_features)
    loss = ((pred[train_mask] - edge_label[train_mask]) ** 2).mean()
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

异构图上的边预测模型的训练

例如想在某一特定类型的边上进行分类任务，用户只需要计算所有节点类型的节点表示， 然后同样通过调用 apply_edges() 方法计算预测值即可。 唯一的区别是在调用 apply_edges 时需要指定边的类型。

class HeteroDotProductPredictor(nn.Module):
    def forward(self, graph, h, etype):
        # h是从5.1节中对每种类型的边所计算的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h   #一次性为所有节点类型的 'h'赋值
            graph.apply_edges(fn.u_dot_v('h', 'h', 'score'), etype=etype)
            return graph.edges[etype].data['score']

同样地，用户也可以编写一个 HeteroMLPPredictor。

class MLPPredictor(nn.Module):
    def __init__(self, in_features, out_classes):
        super().__init__()
        self.W = nn.Linear(in_features * 2, out_classes)

    def apply_edges(self, edges):
        h_u = edges.src['h']
        h_v = edges.dst['h']
        score = self.W(torch.cat([h_u, h_v], 1))
        return {'score': score}

    def forward(self, graph, h, etype):
        # h是从5.1节中对异构图的每种类型的边所计算的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h   #一次性为所有节点类型的 'h'赋值
            graph.apply_edges(self.apply_edges, etype=etype)
            return graph.edges[etype].data['score']

在某种类型的边上为每一条边预测的端到端模型的定义如下所示：

class Model(nn.Module):
    def __init__(self, in_features, hidden_features, out_features, rel_names):
        super().__init__()
        self.sage = RGCN(in_features, hidden_features, out_features, rel_names)
        self.pred = HeteroDotProductPredictor()
    def forward(self, g, x, etype):
        h = self.sage(g, x)
        return self.pred(g, h, etype)

使用模型时只需要简单地向模型提供一个包含节点类型和数据特征的字典。

model = Model(10, 20, 5, hetero_graph.etypes)
user_feats = hetero_graph.nodes['user'].data['feature']
item_feats = hetero_graph.nodes['item'].data['feature']
label = hetero_graph.edges['click'].data['label']
train_mask = hetero_graph.edges['click'].data['train_mask']
node_features = {'user': user_feats, 'item': item_feats}

训练部分和同构图的训练基本一致。例如，如果用户想预测边类型为 click 的边的标签，只需要按下例编写代码。

opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
    pred = model(hetero_graph, node_features, 'click')
    loss = ((pred[train_mask] - label[train_mask]) ** 2).mean()
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

在异构图中预测已有边的类型

预测图中已经存在的边属于哪个类型是一个非常常见的任务类型。例如，根据 本章的异构图样例数据， 用户的任务是给定一条连接 user 节点和 item 节点的边，预测它的类型是 click 还是 dislike。 这个例子是评分预测的一个简化版本，在推荐场景中很常见。

边类型预测的第一步仍然是计算节点表示。可以通过类似 节点分类的RGCN模型 这一章中提到的图卷积网络获得。第二步是计算边上的预测值。 在这里可以复用上述提到的 HeteroDotProductPredictor。 这里需要注意的是输入的图数据不能包含边的类型信息， 因此需要将所要预测的边类型(如 click 和 dislike)合并成一种边的图， 并为每条边计算出每种边类型的可能得分。下面的例子使用一个拥有 user 和 item 两种节点类型和一种边类型的图。该边类型是通过合并所有从 user 到 item 的边类型(如 like 和 dislike)得到。 用户可以很方便地用关系切片的方式创建这个图。

dec_graph = hetero_graph['user', :, 'item']

这个方法会返回一个异构图，它具有 user 和 item 两种节点类型， 以及把它们之间的所有边的类型进行合并后的单一边类型。

由于上面这行代码将原来的边类型存成边特征 dgl.ETYPE，用户可以将它作为标签使用。

edge_label = dec_graph.edata[dgl.ETYPE]

将上述图作为边类型预测模块的输入，用户可以按如下方式编写预测模块：

class HeteroMLPPredictor(nn.Module):
    def __init__(self, in_dims, n_classes):
        super().__init__()
        self.W = nn.Linear(in_dims * 2, n_classes)

    def apply_edges(self, edges):
        x = torch.cat([edges.src['h'], edges.dst['h']], 1)
        y = self.W(x)
        return {'score': y}

    def forward(self, graph, h):
        # h是从5.1节中对异构图的每种类型的边所计算的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h   #一次性为所有节点类型的 'h'赋值
            graph.apply_edges(self.apply_edges)
            return graph.edata['score']

结合了节点表示模块和边类型预测模块的模型如下所示：

class Model(nn.Module):
    def __init__(self, in_features, hidden_features, out_features, rel_names):
        super().__init__()
        self.sage = RGCN(in_features, hidden_features, out_features, rel_names)
        self.pred = HeteroMLPPredictor(out_features, len(rel_names))
    def forward(self, g, x, dec_graph):
        h = self.sage(g, x)
        return self.pred(dec_graph, h)

训练部分如下所示：

model = Model(10, 20, 5, hetero_graph.etypes)
user_feats = hetero_graph.nodes['user'].data['feature']
item_feats = hetero_graph.nodes['item'].data['feature']
node_features = {'user': user_feats, 'item': item_feats}

opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
    logits = model(hetero_graph, node_features, dec_graph)
    loss = F.cross_entropy(logits, edge_label)
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

读者可以进一步参考 Graph Convolutional Matrix Completion 这一示例来了解如何预测异构图中的边类型。 模型实现文件中 的节点表示模块称作 GCMCLayer。边类型预测模块称作 BiDecoder。 虽然这两个模块都比上述的示例代码要复杂，但其基本思想和本章描述的流程是一致的。

5.3 链接预测

在某些场景中，用户可能希望预测给定节点之间是否存在边，这样的任务称作 链接预测 任务。

概述

基于GNN的链接预测模型的基本思想是通过使用所需预测的节点对 u, v 的节点表示 h(L)u 和 h(L)v，计算它们之间存在链接可能性的得分 yu,v。 其中 h(L)u 和 h(L)v 由多层GNN计算得出。

$y_{u,v}=\varphi ({\mathbf{h}}_u^{(L)},{\mathbf{h}}_v^{(L)})$
本节把节点 u 和 v 之间存在连接可能性的 得分 记作 yu,v。

训练一个链接预测模型涉及到比对两个相连接节点之间的得分与任意一对节点之间的得分的差异。 例如，给定一条连接 u 和 v 的边，一个好的模型希望 u 和 v 之间的得分要高于 u 和从一个任意的噪声分布 v’∼Pn(v) 中所采样的节点 v’ 之间的得分。 这样的方法称作 负采样。

许多损失函数都可以实现上述目标，包括但不限于。

交叉熵损失: $\mathcal{L}=-\log \sigma (y_{u,v})-{\sum }_{v_i\sim P_n(v),i=1,\dots ,k}\log \left[1-\sigma (y_{u,v_i})\right]$

贝叶斯个性化排序损失: $\mathcal{L}={\sum }_{v_i\sim P_n(v),i=1,\dots ,k}-\log \sigma (y_{u,v}-y_{u,v_i})$

间隔损失:$\mathcal{L}={\sum }_{v_i\sim P_n(v),i=1,\dots ,k}\max (0,M-y_{u,v}+y_{u,v_i})$, 其中 M 是常数项超参数。

如果用户熟悉 implicit feedback 和 noise-contrastive estimation ， 可能会发现这些工作的想法都很类似。

计算 u 和 v 之间分数的神经网络模型与 5.2 边分类/回归 中所述的边回归模型相同。

下面是使用点积计算边得分的例子。

class DotProductPredictor(nn.Module):
    def forward(self, graph, h):
        # h是从5.1节的GNN模型中计算出的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h
            graph.apply_edges(fn.u_dot_v('h', 'h', 'score'))
            return graph.edata['score']

模型的训练

因为上述的得分预测模型在图上进行计算，用户需要将负采样的样本表示为另外一个图， 其中包含所有负采样的节点对作为边。

下面的例子展示了将负采样的样本表示为一个图。每一条边 (u,v) 都有 k 个对应的负采样样本 (u,vi)，其中 vi 是从均匀分布中采样的。

def construct_negative_graph(graph, k):
    src, dst = graph.edges()

    neg_src = src.repeat_interleave(k)
    neg_dst = torch.randint(0, graph.num_nodes(), (len(src) * k,))
    return dgl.graph((neg_src, neg_dst), num_nodes=graph.num_nodes())

预测边得分的模型和边分类/回归模型中的预测边得分模型相同。

class Model(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        super().__init__()
        self.sage = SAGE(in_features, hidden_features, out_features)
        self.pred = DotProductPredictor()
    def forward(self, g, neg_g, x):
        h = self.sage(g, x)
        return self.pred(g, h), self.pred(neg_g, h)

训练的循环部分里会重复构建负采样图并计算损失函数值。

def compute_loss(pos_score, neg_score):
    # 间隔损失
    n_edges = pos_score.shape[0]
    return (1 - pos_score.unsqueeze(1) + neg_score.view(n_edges, -1)).clamp(min=0).mean()

node_features = graph.ndata['feat']
n_features = node_features.shape[1]
k = 5
model = Model(n_features, 100, 100)
opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
    negative_graph = construct_negative_graph(graph, k)
    pos_score, neg_score = model(graph, negative_graph, node_features)
    loss = compute_loss(pos_score, neg_score)
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

训练后，节点表示可以通过以下代码获取。

node_embeddings = model.sage(graph, node_features)

(实际应用中)，有着许多使用节点嵌入的方法，例如，训练下游任务的分类器，或为相关实体推荐进行最近邻搜索或最大内积搜索。

异构图上的链接预测模型的训练

异构图上的链接预测和同构图上的链接预测没有太大区别。下文是在一种边类型上进行预测， 用户可以很容易地将其拓展为对多种边类型上进行预测。

例如，为某一种边类型，用户可以重复使用 异构图上的边预测模型的训练 里的 HeteroDotProductPredictor 来计算节点间存在连接可能性的得分。

class HeteroDotProductPredictor(nn.Module):
    def forward(self, graph, h, etype):
        # h是从5.1节中对异构图的每种类型的边所计算的节点表示
        with graph.local_scope():
            graph.ndata['h'] = h
            graph.apply_edges(fn.u_dot_v('h', 'h', 'score'), etype=etype)
            return graph.edges[etype].data['score']

要执行负采样，用户可以对要进行链接预测的边类型构造一个负采样图。

def construct_negative_graph(graph, k, etype):
    utype, _, vtype = etype
    src, dst = graph.edges(etype=etype)
    neg_src = src.repeat_interleave(k)
    neg_dst = torch.randint(0, graph.num_nodes(vtype), (len(src) * k,))
    return dgl.heterograph(
        {etype: (neg_src, neg_dst)},
        num_nodes_dict={ntype: graph.num_nodes(ntype) for ntype in graph.ntypes})

该模型与异构图上边分类的模型有些不同，因为用户需要指定在哪种边类型上进行链接预测。

class Model(nn.Module):
    def __init__(self, in_features, hidden_features, out_features, rel_names):
        super().__init__()
        self.sage = RGCN(in_features, hidden_features, out_features, rel_names)
        self.pred = HeteroDotProductPredictor()
    def forward(self, g, neg_g, x, etype):
        h = self.sage(g, x)
        return self.pred(g, h, etype), self.pred(neg_g, h, etype)

训练的循环部分和同构图时一致。

def compute_loss(pos_score, neg_score):
    # 间隔损失
    n_edges = pos_score.shape[0]
    return (1 - pos_score.unsqueeze(1) + neg_score.view(n_edges, -1)).clamp(min=0).mean()

k = 5
model = Model(10, 20, 5, hetero_graph.etypes)
user_feats = hetero_graph.nodes['user'].data['feature']
item_feats = hetero_graph.nodes['item'].data['feature']
node_features = {'user': user_feats, 'item': item_feats}
opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
    negative_graph = construct_negative_graph(hetero_graph, k, ('user', 'click', 'item'))
    pos_score, neg_score = model(hetero_graph, negative_graph, node_features, ('user', 'click', 'item'))
    loss = compute_loss(pos_score, neg_score)
    opt.zero_grad()
    loss.backward()
    opt.step()
    print(loss.item())

5.4 整图分类

许多场景中的图数据是由多个图组成，而不是单个的大图数据。例如不同类型的人群社区。 通过用图刻画同一社区里人与人间的友谊，可以得到多张用于分类的图。 在这个场景里，整图分类模型可以识别社区的类型，即根据结构和整体信息对图进行分类。

概述

整图分类与节点分类或链接预测的主要区别是：预测结果刻画了整个输入图的属性。 与之前的任务类似，用户还是在节点或边上进行消息传递。但不同的是，整图分类任务还需要得到整个图的表示。

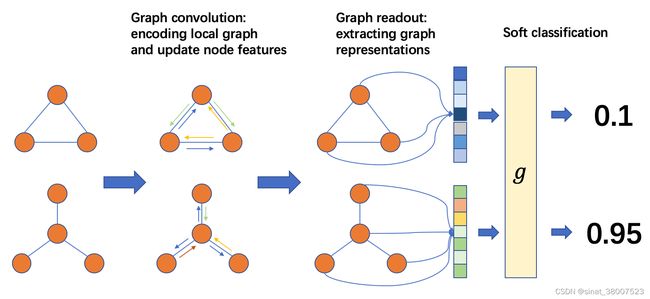
整图分类的处理流程如下图所示：

整图分类流程

从左至右，一般流程是：在这里插入图片描述

准备一个批次的图；

在这个批次的图上进行消息传递以更新节点或边的特征；

将一张图里的节点或边特征聚合成整张图的图表示；

根据任务设计分类层。

批次的图

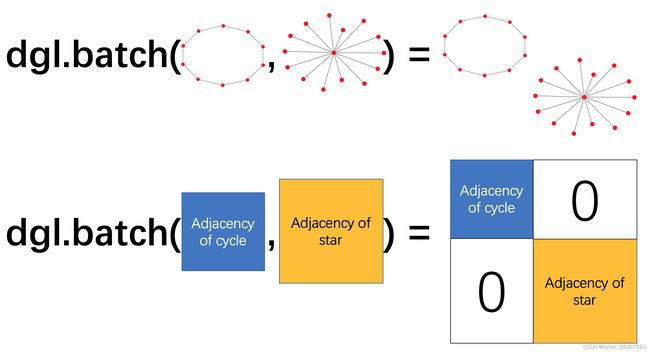
整图分类任务通常需要在很多图上进行训练。如果用户在训练模型时一次仅使用一张图，训练效率会很低。 借用深度学习实践中常用的小批次训练方法，用户可将多张图组成一个批次，在整个图批次上进行一次训练迭代。

使用DGL，用户可将一系列的图建立成一个图批次。一个图批次可以被看作是一张大图，图中的每个连通子图对应一张原始小图。

批次化的图

需要注意，DGL里对图进行变换的函数会去掉图上的批次信息。用户可以通过 dgl.DGLGraph.set_batch_num_nodes() 和 dgl.DGLGraph.set_batch_num_edges() 两个函数在变换后的图上重新加入批次信息。

图读出

数据集中的每一张图都有它独特的结构和节点与边的特征。为了完成单个图的预测，通常会聚合并汇总单个图尽可能多的信息。 这类操作叫做“读出”。常见的聚合方法包括：对所有节点或边特征求和、取平均值、逐元素求最大值或最小值。

给定一张图 g，对它所有节点特征取平均值的聚合读出公式如下：

$h_g=\frac{1}{|\mathcal{V}|}{\sum }_{v\in \mathcal{V}}{h}_v$
其中，hg 是图 g 的表征， V 是图 g 中节点的集合， hv 是节点 v 的特征。

DGL内置了常见的图读出函数，例如 dgl.readout_nodes() 就实现了上述的平均值读出计算。

在得到 hg 后，用户可将其传给一个多层感知机(MLP)来获得分类输出。

编写神经网络模型

模型的输入是带节点和边特征的批次化图。需要注意的是批次化图中的节点和边属性没有批次大小对应的维度。 模型中应特别注意以下几点。

批次化图上的计算

首先，一个批次中不同的图是完全分开的，即任意两个图之间没有边连接。 根据这个良好的性质，所有消息传递函数(的计算)仍然具有相同的结果。

其次，读出函数会分别作用在图批次中的每张图上。假设批次大小为 B，要聚合的特征大小为 D， 则图读出的张量形状为 (B,D)。

import dgl
import torch

g1 = dgl.graph(([0, 1], [1, 0]))
g1.ndata['h'] = torch.tensor([1., 2.])
g2 = dgl.graph(([0, 1], [1, 2]))
g2.ndata['h'] = torch.tensor([1., 2., 3.])

dgl.readout_nodes(g1, 'h')
# tensor([3.])  # 1 + 2

bg = dgl.batch([g1, g2])
dgl.readout_nodes(bg, 'h')
# tensor([3., 6.])  # [1 + 2, 1 + 2 + 3]
最后，批次化图中的每个节点或边特征张量均通过将所有图上的相应特征拼接得到。

bg.ndata['h']
# tensor([1., 2., 1., 2., 3.])

模型定义

了解了上述计算规则后，用户可以定义一个非常简单的模型。

import dgl.nn.pytorch as dglnn
import torch.nn as nn

class Classifier(nn.Module):
    def __init__(self, in_dim, hidden_dim, n_classes):
        super(Classifier, self).__init__()
        self.conv1 = dglnn.GraphConv(in_dim, hidden_dim)
        self.conv2 = dglnn.GraphConv(hidden_dim, hidden_dim)
        self.classify = nn.Linear(hidden_dim, n_classes)

    def forward(self, g, h):
        # 应用图卷积和激活函数
        h = F.relu(self.conv1(g, h))
        h = F.relu(self.conv2(g, h))
        with g.local_scope():
            g.ndata['h'] = h
            # 使用平均读出计算图表示
            hg = dgl.mean_nodes(g, 'h')
            return self.classify(hg)

模型的训练

数据加载

模型定义完成后，用户就可以开始训练模型。由于整图分类处理的是很多相对较小的图，而不是一个大图， 因此通常可以在随机抽取的小批次图上进行高效的训练，而无需设计复杂的图采样算法。

以下例子中使用了 第4章：图数据处理管道 中的整图分类数据集。

import dgl.data
dataset = dgl.data.GINDataset('MUTAG', False)
整图分类数据集里的每个数据点是一个图和它对应标签的元组。为提升数据加载速度， 用户可以调用GraphDataLoader，从而以小批次遍历整个图数据集。

from dgl.dataloading import GraphDataLoader
dataloader = GraphDataLoader(
    dataset,
    batch_size=1024,
    drop_last=False,
    shuffle=True)

训练过程包括遍历dataloader和更新模型参数的部分。

import torch.nn.functional as F

# 这仅是个例子，特征尺寸是7
model = Classifier(7, 20, 5)
opt = torch.optim.Adam(model.parameters())
for epoch in range(20):
    for batched_graph, labels in dataloader:
        feats = batched_graph.ndata['attr']
        logits = model(batched_graph, feats)
        loss = F.cross_entropy(logits, labels)
        opt.zero_grad()
        loss.backward()
        opt.step()

DGL实现了一个整图分类的样例： DGL的GIN样例。 模型训练的代码请参考位于 main.py 源文件中的 train 函数。 模型实现位于 gin.py ， 其中使用了更多的模块组件，例如使用 dgl.nn.pytorch.GINConv 模块作为图卷积层(DGL同样支持它在MXNet和TensorFlow后端里的实现)、批量归一化等。

异构图上的整图分类模型的训练

在异构图上做整图分类和在同构图上做整图分类略有不同。用户除了需要使用异构图卷积模块，还需要在读出函数中聚合不同类别的节点。

以下代码演示了如何对每种节点类型的节点表示取平均值并求和。

class RGCN(nn.Module):
    def __init__(self, in_feats, hid_feats, out_feats, rel_names):
        super().__init__()

        self.conv1 = dglnn.HeteroGraphConv({
            rel: dglnn.GraphConv(in_feats, hid_feats)
            for rel in rel_names}, aggregate='sum')
        self.conv2 = dglnn.HeteroGraphConv({
            rel: dglnn.GraphConv(hid_feats, out_feats)
            for rel in rel_names}, aggregate='sum')

    def forward(self, graph, inputs):
        # inputs是节点的特征
        h = self.conv1(graph, inputs)
        h = {k: F.relu(v) for k, v in h.items()}
        h = self.conv2(graph, h)
        return h

class HeteroClassifier(nn.Module):
    def __init__(self, in_dim, hidden_dim, n_classes, rel_names):
        super().__init__()

        self.rgcn = RGCN(in_dim, hidden_dim, hidden_dim, rel_names)
        self.classify = nn.Linear(hidden_dim, n_classes)

    def forward(self, g):
        h = g.ndata['feat']
        h = self.rgcn(g, h)
        with g.local_scope():
            g.ndata['h'] = h
            # 通过平均读出值来计算单图的表征
            hg = 0
            for ntype in g.ntypes:
                hg = hg + dgl.mean_nodes(g, 'h', ntype=ntype)
            return self.classify(hg)

剩余部分的训练代码和同构图代码相同。

# etypes是一个列表，元素是字符串类型的边类型
model = HeteroClassifier(10, 20, 5, etypes)
opt = torch.optim.Adam(model.parameters())
for epoch in range(20):
    for batched_graph, labels in dataloader:
        logits = model(batched_graph)
        loss = F.cross_entropy(logits, labels)
        opt.zero_grad()
        loss.backward()
        opt.step()

第6章：在大图上的随机（批次）训练

如果用户有包含数百万甚至数十亿个节点或边的大图，通常无法进行 第5章：训练图神经网络 中所述的全图训练。考虑在一个有 N 个节点的图上运行的、隐层大小为 H 的 L 层图卷积网络， 存储隐层表示需要 O(NLH) 的内存空间，当 N 较大时，这很容易超过一块GPU的显存限制。

本章介绍了一种在大图上进行随机小批次训练的方法，可以让用户不用一次性把所有节点特征拷贝到GPU上。

邻居采样方法概述

邻居节点采样的工作流程通常如下：每次梯度下降，选择一个小批次的图节点， 其最终表示将在神经网络的第 L 层进行计算，然后在网络的第 L−1 层选择该批次节点的全部或部分邻居节点。 重复这个过程，直到到达输入层。这个迭代过程会构建计算的依赖关系图，从输出开始，一直到输入，如下图所示：

该方法能节省在大图上训练图神经网络的开销和计算资源。

DGL实现了一些邻居节点采样的方法和使用邻居节点采样训练图神经网络的管道，同时也支持让用户自定义采样策略。

本章路线图

本章的前半部分介绍了不同场景下如何进行随机训练的方法。

6.1 针对节点分类任务的邻居采样训练方法

6.2 针对边分类任务的邻居采样训练方法

6.3 针对链接预测任务的邻居采样训练方法

本章余下的小节介绍了更多的高级主题，面向那些想要开发新的采样算法、 想要实现与小批次训练兼容的图神经网络模块、以及想要了解如何在小批次数据上进行评估和推理模型的用户。

6.4 定制用户自己的邻居采样器

6.5 为小批次训练实现定制化的GNN模块

6.6 超大图上的精准离线推断

第7章：分布式训练

DGL采用完全分布式的方法，可将数据和计算同时分布在一组计算资源中。在本节中， 我们默认使用一个集群的环境设置(即一组机器)。DGL会将一张图划分为多张子图， 集群中的每台机器各自负责一张子图(分区)。为了并行化计算，DGL在集群所有机器上运行相同的训练脚本， 并在同样的机器上运行服务器以将分区数据提供给训练器。

对于训练脚本，DGL提供了分布式的API。它们与小批次训练的API相似。用户仅需对单机小批次训练的代码稍作修改就可实现分布式训练。 以下代码给出了一个用分布式方式训练GraphSage的示例。仅有的代码修改出现在第4-7行：1)初始化DGL的分布式模块，2)创建分布式图对象，以及 3)拆分训练集，并计算本地进程的节点。其余代码保持不变，与 mini_cn-batch training 类似， 包括：创建采样器，模型定义，模型训练的循环。

import dgl
import torch as th

dgl.distributed.initialize('ip_config.txt')
th.distributed.init_process_group(backend='gloo')
g = dgl.distributed.DistGraph('graph_name', 'part_config.json')
pb = g.get_partition_book()
train_nid = dgl.distributed.node_split(g.ndata['train_mask'], pb, force_even=True)

# 创建采样器
sampler = NeighborSampler(g, [10,25],
                          dgl.distributed.sample_neighbors,
                          device)

dataloader = DistDataLoader(
    dataset=train_nid.numpy(),
    batch_size=batch_size,
    collate_fn=sampler.sample_blocks,
    shuffle=True,
    drop_last=False)

# 定义模型和优化器
model = SAGE(in_feats, num_hidden, n_classes, num_layers, F.relu, dropout)
model = th.nn.parallel.DistributedDataParallel(model)
loss_fcn = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=args.lr)

# 模型训练的循环
for epoch in range(args.num_epochs):
    for step, blocks in enumerate(dataloader):
        batch_inputs, batch_labels = load_subtensor(g, blocks[0].srcdata[dgl.NID],
                                                    blocks[-1].dstdata[dgl.NID])
        batch_pred = model(blocks, batch_inputs)
        loss = loss_fcn(batch_pred, batch_labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

在一个集群的机器上运行训练脚本时，DGL提供了一些工具，可将数据复制到集群的计算机上，并在所有机器上启动训练任务。

Note: 当前版本的分布式训练API仅支持PyTorch后端。

Note: 当前版本的实现仅支持具有一种节点类型和一种边类型的图。

DGL实现了一些分布式组件以支持分布式训练，下图显示了这些组件及它们间的相互作用。

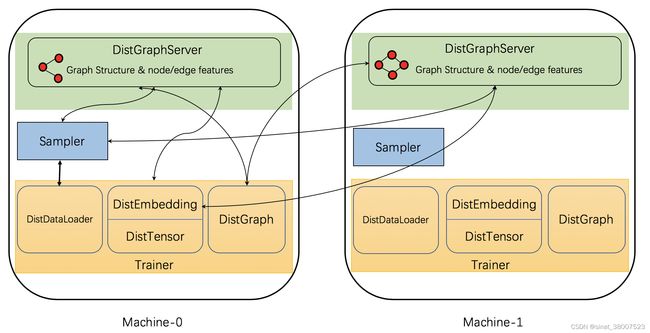
具体来说，DGL的分布式训练具有三种类型的交互进程： 服务器， 采样器 和 训练器。

服务器进程 在存储图分区数据(这包括图结构和节点/边特征)的每台计算机上运行。 这些服务器一起工作以将图数据提供给训练器。请注意，一台机器可能同时运行多个服务器进程，以并行化计算和网络通信。

采样器进程 与服务器进行交互，并对节点和边采样以生成用于训练的小批次数据。

训练器进程 包含多个与服务器交互的类。它用 DistGraph 来获取被划分的图分区数据， 用 DistEmbedding 和 DistTensor 来获取节点/边特征/嵌入，用 DistDataLoader 与采样器进行交互以获得小批次数据。

在初步了解了分布式组件后，本章的剩余部分将介绍以下分布式组件：

7.1 分布式训练所需的图数据预处理

7.2 分布式计算的API

7.3 运行分布式训练/推断所需的工具

参考资料

1. 【DGL教程】第1章 图(Graph)
2. DGL官方教程–API–dgl.DGLGraph