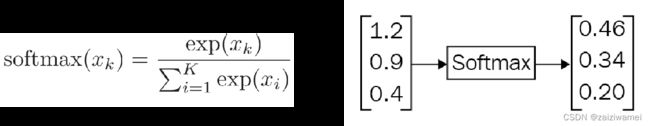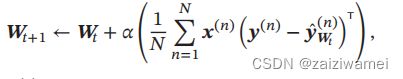第3章 线性模型

系列文章目录

第1章 绪论
第2章 机器学习概述
第3章 线性模型
第4章 前馈神经网络
第5章 卷积神经网络
第6章 循环神经网络
第7章 网络优化与正则化
第8章 注意力机制与外部记忆
第9章 无监督学习
第10章 模型独立的学习方式
第11章 概率图模型
第12章 深度信念网络
第13章 深度生成模型
第14章 深度强化学习
第15章 序列生成模型

---

---

前言

本文对机器学习进行了了一个简要介绍。

---

3.1 分类问题示例

• 图像：图像分类、目标检测、实例分割
• 文本：垃圾邮件过滤、文档归类、情感分析、文本分类、文本情感分类

3. 2 线性分类模型

3.2.1 线性回归模型

$$f(\mathbf{x};\mathbf{w},b)={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

3. 2.2 线性分类模型

3. 2.2.1 二分类

训练集：
$${\{x^{(n)},y^{(n)}\}}_{n=1}^N$$

二分类问题：
$$\begin{gathered} x^{(n)}\in {\mathbf{R}}^D \\ {y}^{(n)}\in \{0,1\} \end{gathered}$$
模型：
$$g(f(\mathbf{x};\mathbf{w}))=\{\begin{array}{l}1,f(\mathbf{x};\mathbf{w})>0\\ 0,f(\mathbf{x};\mathbf{w})<0\end{array}$$

损失函数：0-1损失函数

3. 2.2.2 多分类

训练集：
$${\{x^{(n)},y^{(n)}\}}_{n=1}^N$$

多分类问题：
$$\begin{gathered} x^{(n)}\in {\mathbf{R}}^D \\ {y}^{(n)}\in \{0,1，\dots ，C\} \end{gathered}$$
模型：

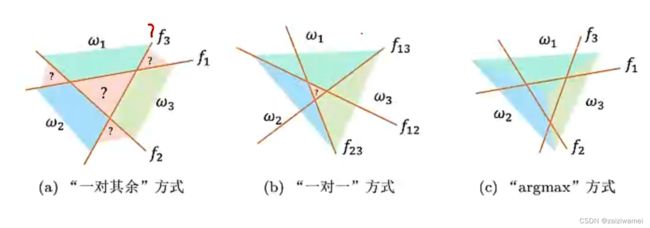
一对其余方式: 类似树状分类法，构建C个分类器。
一对一方式：每两个类之间建立一个分类器，共构建C(C-1)/2个分类器。
argmax方式：数据在哪个类下得分最高，分为哪个类。

3.2.3 线性模型

Logistic 回归
Softmax 回归
感知机
支持向量机

3. 3 交叉熵与对数似然

熵：
随机变量X的自信息的数学期望。

交叉熵：
交叉熵是按照概率分布q的最优编码对真实分布为p的信息进行编码的长度。

KL散度（Kullback-Leibler Divergence）：

• KL散度是用概率分布q来近似p时所造成的信息损失量。
• KL散度是按照概率分布q的最优编码对真实分布为p的信息进行编码，其平均编码长度（即交叉熵）H(p,q)和p的最优平均编码长度（即熵）H (p)之间的差异。

负对数似然

3.4 Logistic 回归

原理：Logistic 回归也称为对数几率回归，由于原有损失函数无法求导，从而进行权重优化，所以利用概率思想将分类问题转化为条件概率估计问题，从而进行问题求解。

Logistic 函数
$$f(x)=\frac{1}{1+exp(-x)}$$

3.4.1 分类问题转化

将分类问题看做条件概率估计问题
用非线性函数g来预测类别标签的条件概率p(y=c|x).
以二分类为例:
$$p_{\theta }(y=1\mid x)\to g(f(x;w))$$
激活函数g将线性函数的值域从实数空间“挤压”到了（0,1）之间。

使用Logistic 回归函数，模型变为

$$g(f(\mathbf{x};\mathbf{w}))=\frac{1}{1+exp(-f(\mathbf{x};\mathbf{w}))}$$

计算单个变量实际值与预测值之间的差异：

$$H(p_r,p_{\theta })=-(y^{\ast }\log \hat{y}+(1-y^{\ast })\log (1-\hat{y}))$$

式中：
$p_{\theta }$为模型预测条件概率，$\hat{y}$为预测结果
$p_r$为真实条件概率，y*为样本真实结果

3.4.2 梯度下降

交叉熵损失函数，模型在训练集的风险函数为：

梯度为

权重更新

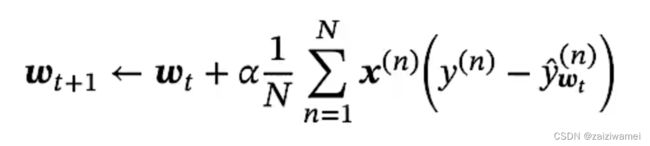
3.5 Softmax 回归

Softmax函数

3.5.1 分类问题转化概率问题

适用于多分类问题

对于多类别问题，类别标签y$\in$可以有C个取值。

模型为：

使用softmax函数，目标类别y=c的条件概率为：

对于各个分类，向量表示softmax：

计算所有分类的交叉熵损失：

3.5.2 梯度下降

损失函数为：

求解梯度

权重更新

3.6 感知机

3.6.1 模型

模拟生物神经元行为的机器，有与生物神经元相对应的部件，如权重（突触）、偏置（阈值）及激活函数（细胞体），输出为+1或-1。

预测输出结果为：
$$\hat{y}=sgn({\mathbf{w}}^{T}x),即\hat{y}=\{\begin{array}{l}+1,{\mathbf{w}}^{T}x>0\\ -1,{\mathbf{w}}^{T}x\le 0\end{array}$$

3.6.2 学习目标

训练集为$\{(x^{(n)},y^{(n))}{\}}_{n=1}^N$,找到权重$\mathbf{w}\ast$使得

$$y^{(n)}\mathbf{w}{\ast }^T{x}^{(n)}>0,n\in \{1,\dots ,N\}$$

3.6.3 学习算法

• 先初始化一个权重向量w←0（通常是全零向量）
• 每次分错一个样本(x,y)时，即
  $$y{\mathbf{w}}^{T}x<0$$
• 用这个样本来更新权重
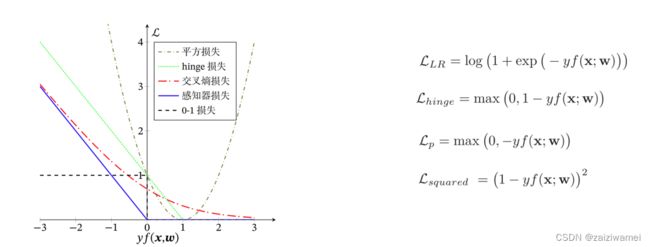
  $$\mathbf{w}\leftarrow \mathbf{w}+y\mathbf{x}$$
• 根据感知器的学习策略，可以反推出感知器的损失函数为
  

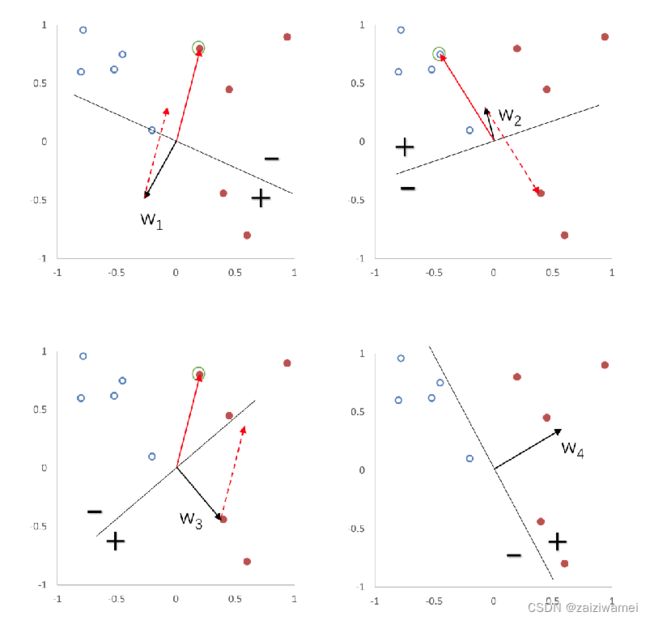
3.6.4 感知器的学习过程

3.6.5 感知器参数学习的更新过程

3.6.5 感知器参数学习的更新过程

3.7 支持向量机

间隔：
决策边界到分类样本的最短距离。
数据集D中每个样本$x^{(n)}$到分隔超平面的距离为：
$${\gamma }^{(n)}=\frac{\Vert {\mathbf{w}}^T{x}^{(n)}+b\Vert }{\Vert \mathbf{w}\Vert }=\frac{y^{(n)}({\mathbf{w}}^T{x}^{(n)}+b)}{\Vert \mathbf{w}\Vert }$$

选择间隔最大的决策边界，即寻找超平面（$\mathbf{w}\ast ,b\ast$）使得$\gamma$最大。



软间隔

3.8 线性分类模型小结

类别
不同损失函数的对比

---

总结