DQN理论基础及其代码实现【Pytorch + CartPole-v0】
DQN算法的理论基础
基于动态规划方法、基于蒙特卡罗方法和基于时间差分的方法都有一个基本的前提条件:状态空间和动作空间是离散的,而且状态空间和动作空间不能太大。这些强化学习方法的基本步骤是先评估值函数,再利用值函数改善当前的策略。这时的值函数其实是一个表格,对于状态值函数,其索引是状态,对于行为值函数,其索引是状态行为对。值函数的更新迭代实际上就是这张表的迭代更新。
若状态空间的维数很大,或者状态空间为连续空间,此时值函数无法用一张表格来表示。这时,我们需要利用函数逼近的方法表示值函数。
在值函数逼近方法中,值函数对应着一个逼近函数 v ^ ( s ) \hat v(s) v^(s)。从数学角度来看,函数逼近方法可以分为参数逼近和非参数逼近,因此强化学习值函数估计可以分为参数化逼近和非参数化逼近。其中参数化逼近又分为线性参数化逼近和非线性化参数逼近。
所谓参数化逼近,是指值函数可以由一组参数 θ \mathbb{\theta} θ来近似。我们将逼近的值函数写为: v ^ ( s , θ ) \hat v(s,\theta) v^(s,θ)。
当逼近的值函数结构确定时(如线性逼近时选定了基函数,非线性逼近时选定了神经网络的结构),那么值函数的逼近就等价于参数的逼近。值函数的更新也就等价于参数的更新。也就是说,我们需要利用试验数据来更新参数值。
DQN算法的大体框架是传统强化学习中的Q-Learning,Q-Learning算法是异策略的时间差分方法。异策略是指行动策略和要评估的策略不是一个策略。
Q-Learning的行动策略是 ϵ -greedy \epsilon\text{-greedy} ϵ-greedy策略,要评估和改进的策略是贪婪策略。
DQN算法对Q-Learning的修改主要体现在以下三个方面:
卷积神经网络
DQN的行为值函数利用神经网络逼近,属于非线性逼近。此处的值函数对应着一组参数,在神经网络里参数是每层网络的权重,用 θ \theta θ表示。用公式表示的话,值函数为 Q ( s , a ; θ ) Q(s,a;\theta) Q(s,a;θ),此时更新值函数其实是更新参数 θ \theta θ,当网络结构确定时, θ \theta θ就代表值函数。
事实上,利用神经网络逼近值函数的做法在强化学习领域早就存在了,但当时学者们发现利用神经网络,尤其是深度神经网络逼近值函数不太靠谱,因为常常出现不稳定不收敛的情况,直到DeepMind的出现,DeepMind的创始人Hassabis将神经科学的成果应用到了深度神经网络的训练之中。
经验回放
在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。在原来的 Q-learning 算法中,每一个数据只会用来更新一次值。为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法,具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用。
- 使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。
- 提高样本效率。每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
目标网络
与传统的Q-Learning算法不同的是,利用神经网络对值函数进行逼近时,值函数的更新步更新的时参数 θ \theta θ,DQN利用了卷积神经网络,其更新方法是SGD,因此值函数更新实际上变成了监督学习的一次更新过程,其梯度下降法为:
θ t + 1 = θ t + α [ r + γ max a ′ Q ( s ′ , a ′ , θ ) − Q ( s , a ; θ ) ] ▽ Q ( s , a ; θ ) \theta_{t+1}=\theta_t+\alpha[r+\gamma\max_{a'}Q(s',a',\theta)-Q(s,a;\theta)]\bigtriangledown Q(s,a;\theta) θt+1=θt+α[r+γa′maxQ(s′,a′,θ)−Q(s,a;θ)]▽Q(s,a;θ)
其中, r + γ max a ′ Q ( s ′ , a ′ , θ ) r+\gamma\max_{a'}Q(s',a',\theta) r+γmaxa′Q(s′,a′,θ)为TD目标,在计算 max a ′ Q ( s ′ , a ′ , θ ) \max_{a'}Q(s',a',\theta) maxa′Q(s′,a′,θ)值时要用到的网络参数为 θ \theta θ。
我们称计算TD目标时所用的网络为TD网络。在DQN算法出现之前,利用神经网络逼近值函数时,计算TD目标的动作值函数所用的网络参数 θ \theta θ,与梯度计算中要逼近的值函数所用的网络参数相同,这样就容易导致数据间存在关联性,从而使训练不稳定。
为了解决此问题,DeepMind提出了计算TD目标的网络表示为 θ − \theta^- θ−,计算值函数逼近的网络表示为 θ \theta θ。用于动作值函数逼近的网络每一步都更新,而用于计算TD目标的网络则是每个固定的步数更新一次。
因此值函数的更新变为:
θ t + 1 = θ t + α [ r + γ max a ′ Q ( s ′ , a ′ , θ − ) − Q ( s , a ; θ ) ] ▽ Q ( s , a ; θ ) \theta_{t+1}=\theta_t+\alpha[r+\gamma\max_{a'}Q(s',a',\theta^-)-Q(s,a;\theta)]\bigtriangledown Q(s,a;\theta) θt+1=θt+α[r+γa′maxQ(s′,a′,θ−)−Q(s,a;θ)]▽Q(s,a;θ)
基于CartPole环境的DQN复现
环境介绍
本次以下图所示的所示的车杆(CartPole)环境为例,它的状态值就是连续的,动作值是离散的。

环境介绍:在车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束。智能体的状态是一个维数为 4 的向量,每一维都是连续的,其动作是离散的,动作空间大小为 2,在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数。
CartPole环境的状态空间
| 维度 | 意义 | 最小值 | 最大值 |
|---|---|---|---|
| 0 | 车的位置 | -2.4 | 2.4 |
| 1 | 车的速度 | -Inf | Inf |
| 2 | 杆的角度 | ~ -41.8° | ~ 41.8° |
| 3 | 杆尖端的速度 | -Inf | Inf |
CartPole环境的动作空间
| 标号 | 动作 |
|---|---|
| 0 | 向左移动小车 |
| 1 | 向右移动小车 |
Q网络
这里定义一个简单的网络就行了,毕竟环境不是很复杂。注意输出维度,这里动作有两类,所以输出维度设为2就行了。
class Qnet(nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.layer = nn.Sequential(
nn.Linear(state_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, action_dim)
)
def forward(self, s):
s = self.layer(s)
return s
变量定义
这里定义一些DQN需要的参数,以及Q网络,优化器的定义。
def __init__(self, args):
self.args = args
self.hidden_dim = 128
self.batch_size = args.batch_size
self.lr = args.lr
self.gamma = args.gamma # 折扣因子
self.epsilon = args.epsilon # epsilon-贪婪策略
self.target_update = args.target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.num_episodes = args.num_episodes
self.minimal_size = args.minimal_size
self.env = gym.make(args.env_name)
random.seed(args.seed)
np.random.seed(args.seed)
self.env.seed(args.seed)
torch.manual_seed(args.seed)
self.replay_buffer = ReplayBuffer(args.buffer_size)
self.state_dim = self.env.observation_space.shape[0]
self.action_dim = self.env.action_space.n
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)
self.target_q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)
self.optimizer = Adam(self.q_net.parameters(), lr=self.lr)
动作选择函数
基于epsilon-贪婪策略选择动作。如下代码应该很好理解。在Q网络输出时,选择最大值对应的索引即为动作。(可以理解Q网络的输出为动作对应的概率,这里肯定不是概率,毕竟网络的输出都没有归一化的0~1之间,但这样理解没啥问题)
def select_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
DQN更新函数
网络的更新函数,先从经验池采样一批样本,将样本转为Tensor格式,传入Q网络,计算TD-error,利用MSE损失函数更新网络参数,这些都没啥好说的。而且这里的代码其实跟Q-Learning差不多,只是换成了神经网络而已。另外,目标网络需要每个一定轮数更新一次,这里的更新其实就是把Q网络的参数拷贝过来,也很好理解。
def update(self, transition):
states = torch.tensor(transition["states"], dtype=torch.float).to(self.device)
actions = torch.tensor(transition["actions"]).view(-1, 1).to(self.device)
rewards = torch.tensor(transition["rewards"], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition["next_states"], dtype=torch.float).to(self.device)
dones = torch.tensor(transition["dones"], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q value
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1) # 下个状态的最大Q值
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD error
loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1
这里有一个函数需要解释一下,就是第8行的gather()函数,这个函数经常用于Softmax多分类的场景。简单解释一下这里的作用。来看一个demo,下面是模拟的update函数的功能。
>>> q_value = torch.randn(8,2)
>>> action = torch.argmax(q_value, dim=1)
>>> action = action.view(-1, 1)
>>> action
tensor([[0],
[1],
[1],
[1],
[1],
[0],
[0],
[1]])
>>> q_value
tensor([[ 2.5824, 0.8468],
[-0.0568, 0.0458],
[-0.1389, -0.0529],
[-0.6203, 0.5162],
[-0.0820, 1.8751],
[ 0.9972, 0.2555],
[-0.7126, -0.9540],
[-1.0091, 0.8833]])
>>> q_value.gather(1, action)
tensor([[ 2.5824],
[ 0.0458],
[-0.0529],
[ 0.5162],
[ 1.8751],
[ 0.9972],
[-0.7126],
[ 0.8833]])
在update()中选择动作函数的输出加了argmax函数,其实也就相当于demo中的action。可以看到gather函数的作用就是根据action的索引来选取值。比如action的第一个值是0,那么gather作用后的第一行的值就是q_value第一行第一列的值。这下懂了吧。这也是上面我说的为啥这个函数多用于多分类场景,毕竟在多分类场景下,神经网络的输出层一般会加上一个softmax输出0~1之间的概率,最后根据这个概率最大的输出对应的预测的类别。
DQN运行函数
这里没啥可说的,训练函数都大差不差的,自己看~
def run(self):
return_list = []
for i in range(10):
with tqdm(total=int(self.num_episodes / 10), desc=f'Iteration {i}') as pbar:
for episode in range(self.num_episodes // 10):
episode_return = 0
state = self.env.reset()
while True:
action = self.select_action(state)
next_state, reward, done, _ = self.env.step(action)
self.replay_buffer.add(state, action, reward, next_state, done)
if self.replay_buffer.size() > self.minimal_size:
s, a, r, s_, d = self.replay_buffer.sample(self.batch_size)
transitions = {"states": s, "actions": a, "rewards": r, "next_states": s_, "dones": d}
self.update(transitions)
state = next_state
episode_return += reward
if done: break
return_list.append(episode_return)
if (episode + 1) % 10 == 0:
pbar.set_postfix(
{
"episode": f"{self.num_episodes / 10 * i + episode + 1}",
"return": f"{np.mean(return_list[-10:]):3f}"
}
)
pbar.update(1)
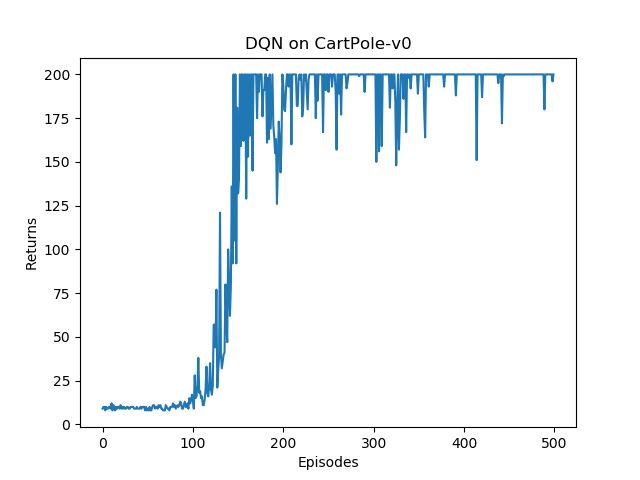
运行结果
完整代码实现
import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import torch.nn as nn
from torch.optim import Adam
import argparse
class ReplayBuffer:
"""经验回放池"""
def __init__(self, capacity):
self.buffer = deque(maxlen=capacity) # 队列,先进先出
# 将数据加入buffer
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
# 从buffer中采样数据,数量为batch_size
def sample(self, batch_size):
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
# 目前buffer中数据的数量
def size(self):
return len(self.buffer)
def moving_average(a, window_size):
"""滑动平均"""
cumulative_sum = np.cumsum(np.insert(a, 0, 0))
middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
r = np.arange(1, window_size - 1, 2)
begin = np.cumsum(a[:window_size - 1])[::2] / r
end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
return np.concatenate((begin, middle, end))
def define_args():
parser = argparse.ArgumentParser(description='DQN parametes settings')
parser.add_argument('--batch_size', type=int, default=64, metavar='N', help='batch size')
parser.add_argument('--lr', type=float, default=2e-3, help='Learning rate for the net.')
parser.add_argument('--num_episodes', type=int, default=500, help='the num of train epochs')
parser.add_argument('--seed', type=int, default=0, metavar='S', help='Random seed.')
parser.add_argument('--gamma', type=float, default=0.98, metavar='S', help='the discount rate')
parser.add_argument('--epsilon', type=float, default=0.01, metavar='S', help='the epsilon rate')
parser.add_argument('--target_update', type=float, default=10, metavar='S', help='the frequency of the target net')
parser.add_argument('--buffer_size', type=float, default=10000, metavar='S', help='the size of the buffer')
parser.add_argument('--minimal_size', type=float, default=500, metavar='S', help='the minimal size of the learning')
parser.add_argument('--env_name', type=str, default="CartPole-v0", metavar='S', help='the name of the environment')
args = parser.parse_args()
return args
class Qnet(nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.layer = nn.Sequential(
nn.Linear(state_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, action_dim)
)
def forward(self, s):
s = self.layer(s)
return s
class DQN:
def __init__(self, args):
self.args = args
self.hidden_dim = 128
self.batch_size = args.batch_size
self.lr = args.lr
self.gamma = args.gamma # 折扣因子
self.epsilon = args.epsilon # epsilon-贪婪策略
self.target_update = args.target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.num_episodes = args.num_episodes
self.minimal_size = args.minimal_size
self.env = gym.make(args.env_name)
random.seed(args.seed)
np.random.seed(args.seed)
self.env.seed(args.seed)
torch.manual_seed(args.seed)
self.replay_buffer = ReplayBuffer(args.buffer_size)
self.state_dim = self.env.observation_space.shape[0]
self.action_dim = self.env.action_space.n
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)
self.target_q_net = Qnet(self.state_dim, self.hidden_dim, self.action_dim).to(self.device)
self.optimizer = Adam(self.q_net.parameters(), lr=self.lr)
def select_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition):
states = torch.tensor(transition["states"], dtype=torch.float).to(self.device)
actions = torch.tensor(transition["actions"]).view(-1, 1).to(self.device)
rewards = torch.tensor(transition["rewards"], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition["next_states"], dtype=torch.float).to(self.device)
dones = torch.tensor(transition["dones"], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q value
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1) # 下个状态的最大Q值
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD error
loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1
def run(self):
return_list = []
for i in range(10):
with tqdm(total=int(self.num_episodes / 10), desc=f'Iteration {i}') as pbar:
for episode in range(self.num_episodes // 10):
episode_return = 0
state = self.env.reset()
while True:
action = self.select_action(state)
next_state, reward, done, _ = self.env.step(action)
self.replay_buffer.add(state, action, reward, next_state, done)
if self.replay_buffer.size() > self.minimal_size:
s, a, r, s_, d = self.replay_buffer.sample(self.batch_size)
transitions = {"states": s, "actions": a, "rewards": r, "next_states": s_, "dones": d}
self.update(transitions)
state = next_state
episode_return += reward
if done: break
return_list.append(episode_return)
if (episode + 1) % 10 == 0:
pbar.set_postfix(
{
"episode": f"{self.num_episodes / 10 * i + episode + 1}",
"return": f"{np.mean(return_list[-10:]):3f}"
}
)
pbar.update(1)
self.plot_reward(return_list)
def plot_reward(self, reward_list):
episodes_list = list(range(len(reward_list)))
plt.plot(episodes_list, reward_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(self.args.env_name))
plt.show()
mv_return = moving_average(reward_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(self.args.env_name))
plt.show()
if __name__ == '__main__':
args = define_args()
model = DQN(args)
model.run()
\quad
\quad
\quad
持续更新~有错误的话敬请指正!