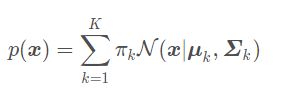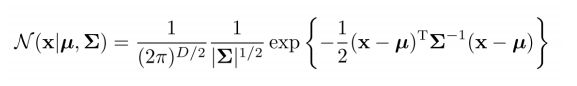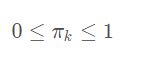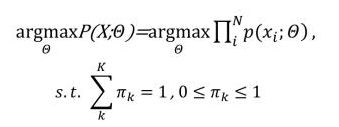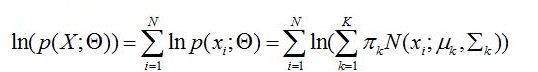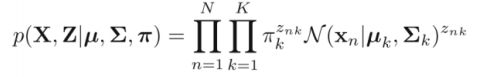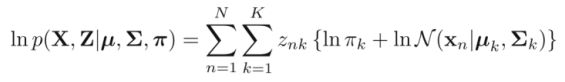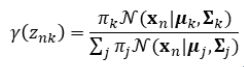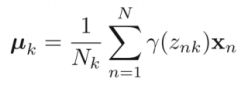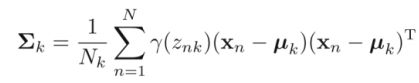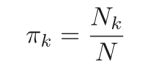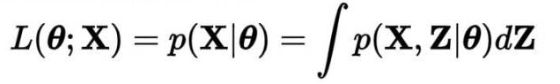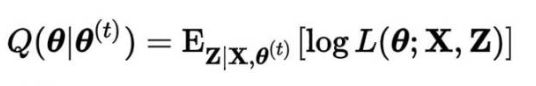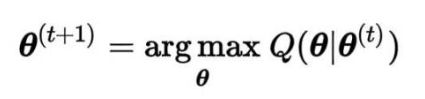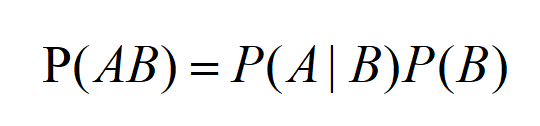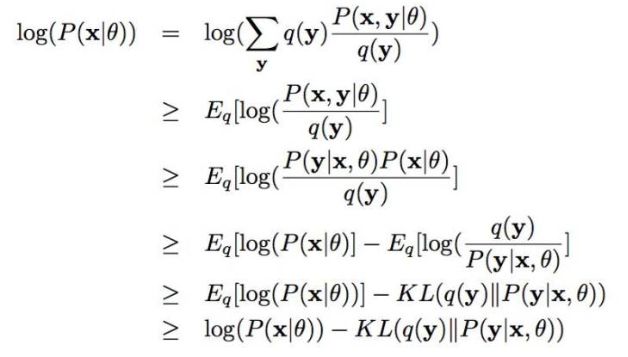AI大语音(六)——混合高斯模型(GMM)(深度解析)
本文来自公众号“AI大道理”。
这里既有AI,又有生活大道理,无数渺小的思考填满了一生。
1 GMM基础
高斯混合模型(GMM)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况。
灵魂的拷问:为什么GMM可以拟合出任意类型的分布?
AI大语音:不仅GMM可以,只要性质不太奇怪的混合模型一般都能近似任意分布。这个思想和泰勒展开、傅里叶变换是类似的,任何波形都可以用正弦波叠加表示,而且频率还是基频的整数倍。
利用高斯混合模型进行聚类,本质上可以这么理解:
数据的分布由若干高斯分布组合而成,需要通过传入的无标记数据,求解出各个高斯模型的参数和各个模型的先验概率!不同于一般利用最大似然估计参数的情况在于由于传入的数据无标记,也就是说缺少了观测数据的类别这个隐藏信息,所以这个隐藏信息的概率分布也成了估计内容之一,从而无法通过求偏导进行梯度下降来求解,于是利用了EM。
设有随机变量X,则混合高斯模型可以用下式表示:
其中N(x∣μk,Σk)称为混合模型中的第k个分量。
其中, ∈ ,为高斯分布的均值向量, ∈ ×,为高斯分布的协方差矩阵。
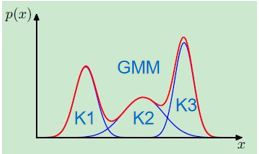
若有三个聚类,可以用三个二维高斯分布来表示,那么分量数K=3。 πk是混合系数,且满足:
![]()
可以认为πk就是每个分量N(x∣μk,Σk)的权重。
2 GMM的隐变量
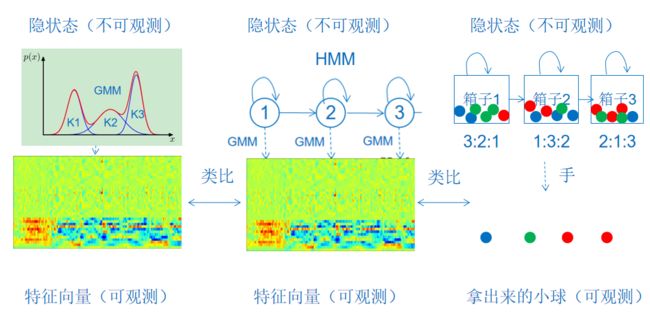
隐变量是一个辅助变量,GMM的隐变量表示的是样本x属于哪一个高斯分布。
隐变量是一个向量,并且这个向量中只有一个元素取值为1,其它的都是0。因为假设只有一个高斯分量被选中并产生观测数据。然而我们的GMM的一个观测数据在直观上应该是每个高斯分量都有产生,而不是由一个高斯分量单独生成,只是重要性不同(由系数控制)
假设我们知道数据可以分为两类,在随机抽取一个数据点,不知道这个数据来自第一类还是第二类,类比GMM中K1、K2的高斯分模型,不知道数据来自哪个分模型。
隐变量就是为了描述数据归属看不见这个现象的。
隐变量是一个离散的随机变量。
GMM中K1、K2、K3类比箱子1、箱子2、箱子3,类比HMM中状态1、状态2、状态3。
3 GMM训练问题
极大似然估计、EM
1) 极大似然估计
利用不完全数据(只有观测数据)的边缘分布。
给定一些观测数据X={x},假设{x}符合混合高斯分布:
求解一组混合高斯模型的参数使得:
对目标函数取对数:
对数似然函数分别对参数, , 求导,使得导数等于0,来更新参数。
目标函数是和的对数,这时候求导比较困难,形式复杂,同时,还有个问题就是求一个参数的时候会依赖其他参数的值,但是其他参数的值其实也是未知的,也是待估计的。
因此需要EM算法。
2)EM算法估计
利用完全数据的联合概率分布。
完全数据的似然函数:
取对数:
计算的后验概率:
完全数据的对数似然关于潜变量的期望值Q函数:
对参数, , 求导,使得导数等于0,来更新参数。(过程中应用到拉格朗日乘子法)
4 EM算法深入理解
第一层:E期望+M最大化(看山是山)(直观理解)
所谓直观理解就是将EM分成E步+M步进行组合。
隐变量的似然度:
E-step:
M-step:
第二层:局部下限构造(看山是沙)(细致入微)
细致入微看看E步M步的本质。
补充三个知识:
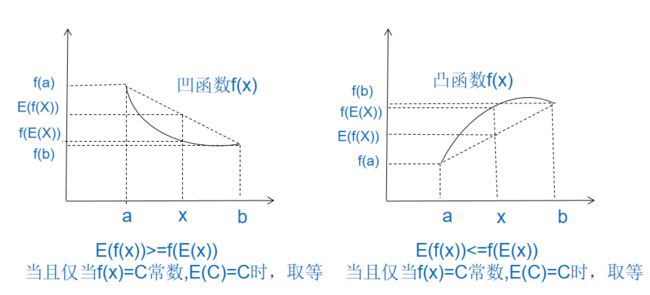
a) Jenson不等式
若f(x)为严格凹函数,X为实值随机变量,且期望存在,则下述不等式成立:
f(E(X))<=E(f(X))
当且仅当X≡E(X),即X为常数时,不等式取等号。
Jensen不等式应用于凸函数时,不等号方向反向,也就是:
f(E(X))>=E(f(X))、
(AI大道理:很多资料将左图称为凸函数,右图称为凹函数,这是翻译问题,不必理会。见图判断最准确。)
b) 条件概率
c) 联合分布求和等于边缘分布
深入到基于隐变量的EM算法的收敛性证明, 基于log(x)函数的Jensen不等式构造, 容易证明,EM算法是在反复的构造新的下限,然后进一步求解。
利用补充知识a)的Jenson不等式:
什么是KL散度?KL散度 是衡量两个概率分布之 间差异的一个度量。
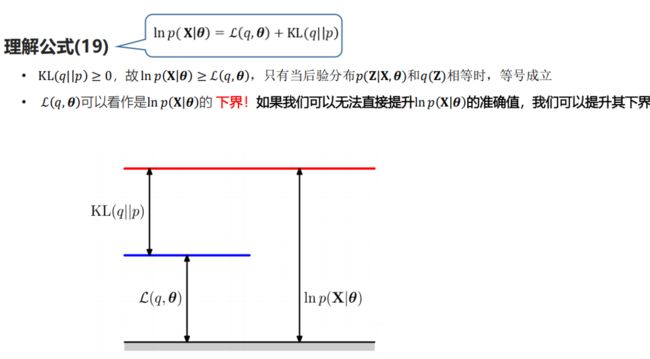
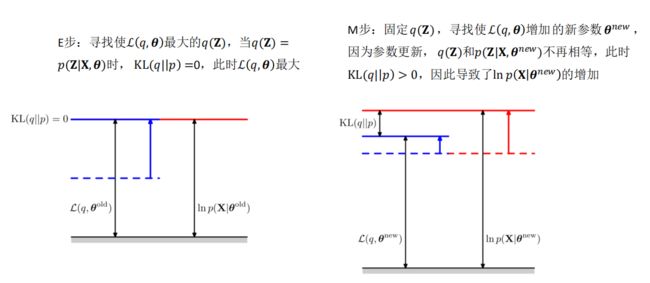
在之前的EM算法中,E步所计算的 (, )实际上等价于计算ℒ( , )
从参数空间理解EM算法:
红线表示观测数据的对数似然,蓝线表示在原始参数下,下边界ℒ (q, θ )的变化,在M步,最大化下边界ℒ (q, θ) 关于参数θ,得到新的参数,此时得到的新的下边界绿线所示,继续进行E步和M步,直到达到观测数据的最大似然。
先固定当前参数, 计算得到当前隐变量分布的一个下届函数, 然后优化这个函数, 得到新的参数, 然后循环继续。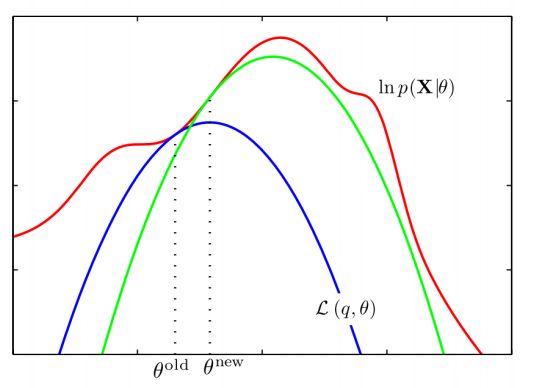
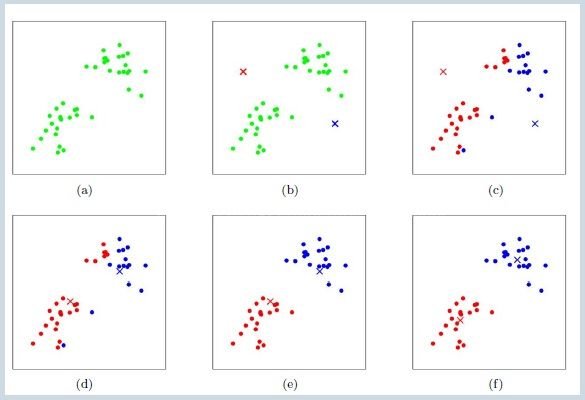
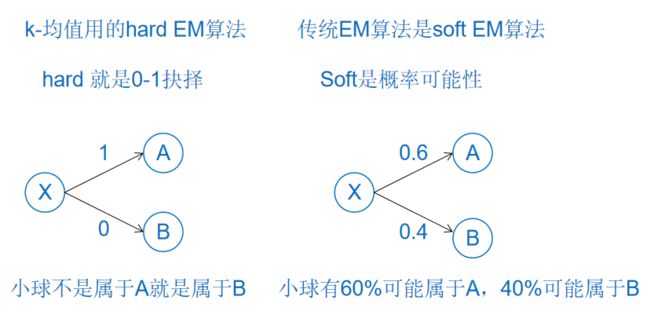
第三层:K-均值方法是一种Hard EM算法(看峰是山)(举一反三)
举一反三,概率的极端是0和1,那么K-means也是EM算法的一种。
k均值聚类算法是一种迭代求解的聚类分析算法,其步骤是:
k均值聚类是使用最大期望算法。
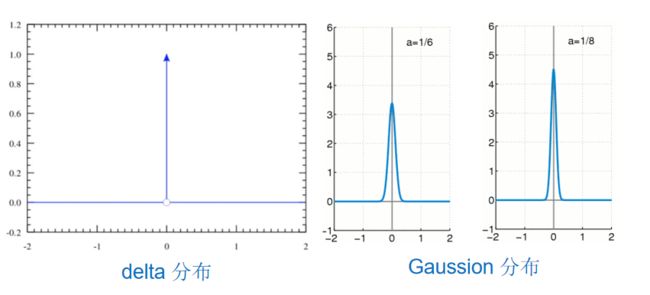
K-均值在讨论隐变量的决定时候,用的是dirac delta 分布, 这个分布是高斯分布的一种极限。
第四层:EM 是 广义EM的特例(看山是群山峻岭)
广义EM包括传统EM和类似K-means算法的其他EM。
充分理解了k-均值和EM算法本身的演化和差异可以理解到隐变量是存在一种分布的。
跨过隐变量, 进入隐分布的境界。
只要满足E步骤是固定参数优化隐分布, M步骤是固定隐分布优化参数,都是广义EM算法。
附录(魔鬼写手)
——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号
—————————————————————
![]()
—————————————————————
投稿吧 | 留言吧
▼
下期预告
▼
AI大语音(七)——基于GMM的0—9语音识别系统
▼
往期精彩回顾
▼
AI大语音(一)——语音识别基础
AI大语音(二)——语音预处理
AI大语音(三)——傅里叶变换家族
AI大语音(四)——MFCC特征提取
AI大语音(五)——隐马尔科夫模型(HMM)