T检验、F检验、卡方检验、互信息法及机器学习应用

1、T检验

目的：主要是为了比较数据样本之间是否具有显著性的差异。主要通过样本均值的差异进行检验，判断差异性。

前置条件：样本服从正态分布；各样本间独立。

适用：小样本（n<30）; 定量数据检测

T检验三种方式：

• 单一样本T检验

  检验一组样本数据均值与已知总体均值是否存在差异。

  eg: 验证矿泉水瓶容量是否为550ML？

  现在有16个矿泉水瓶样本，分别为558、551、542、557、552、547、551、549、548、551、553、557、548、550、546、552
  $$\begin{array}{l}统计量计算：\\ 1.计算样本均值：\overline{X}=(558+551+...+552)/8=550.75\\ 2.计算样本标准差：S=\sqrt{\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n}}\\ 3.计算统计量：\frac{\overline{X}-\mu }{s/\sqrt{n}}\mu :总体均值\\ 4.查表对比。\\ 根据统计量计算公式：统计量越小，差异越小。\end{array}$$

• 独立样本T检验

  检验两组非相关样本数据的差异性（两组样本数据的均值是否相等）。需要先判断方差是否相等。

  eg: 验证两个不同车间生产的矿泉水瓶容量的差异。

  再来一组16个矿泉水瓶样本，分别为555、553…551
  $$\begin{gathered} 统计量计算：t=\frac{\overline{x_1}-\overline{x_2}}{\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}} \\ 从统计量看：t越小两组数据差异越小 \end{gathered}$$

• 配对T检验

  检验一组样本数据在不同条件或不同时间下的差异性。要求两组数据样本量相同。

  eg: 验证同一个生产间上一月与下一月生产的矿泉水瓶容量的差异。

  7月生产的4个矿泉水瓶容量为551、553、549、547。

  8月生产的4个矿泉水瓶容量为552、553、548、547。
  $$\begin{array}{l}统计量计算：\\ 1.计算两组样本数据差值d：即551-552,553-553,549-548,547-547\\ 2.计算差值平均数：\overline{d}=(-1+0+1+0)/4=0\\ 2.计算样本标准差：S_d=\sqrt{\frac{{\sum }_{i=1}^n(d_i-\overline{d}{)}^2}{n-1}}\\ 3.计算统计量：\frac{\overline{d}-\mu }{s_d/\sqrt{n}}\mu :理论总体差值均值0(同一车间生产容量应该一样)\\ 4.查表对比。\\ 根据统计量计算公式：统计量越小，差异越小。\end{array}$$

2、F检验（方差分析，用于特征筛选）

目的：判断两个样本的总体方差是否相等。

公式：
$$\begin{gathered} 样本1方差：S_1^2=\frac{x-\overline{x}}{n-1} \\ 样本2方差:S_2^2=\frac{x-\overline{x}}{n-1} \\ 统计量：F=\frac{max\{S_1^2,S_2^2\}}{min\{S_1^2,S_2^2\}} \end{gathered}$$
eg：客户满意度是否和行业因素有关（单因素方差分析）。

import pandas as pd
# 样本数据生成
data = pd.DataFrame({'行业':['零售业','旅游业','航空','制造业'],
                     '满意度':[[57,66,49,40,34,53,44],
                               [68,39,29,45,56,51],
                               [31,49,21,34,40],
                               [44,51,65,77,58]]})
print(data)
'''
    行业	      满意度
0	零售业	[57, 66, 49, 40, 34, 53, 44]
1	旅游业	[68, 39, 29, 45, 56, 51]
2	航空	[31, 49, 21, 34, 40]
3	制造业	[44, 51, 65, 77, 58]
'''

'''
1. 同行业之间的误差，称为组内误差（SSE）,组内误差可以认为是随机误差。
2. 不同行业之间的误差，称之为组间误差(SSA)，若被投诉次数与行业无关，不同行业抽样也来自同一整体，组间也只有随机误差；若被投诉次数与行业因素相关，组间误差就包含随机误差和因素误差。
3. 当检验不同行业间均值是否相等，其实就是检验组间的误差大不大
''' 
## 计算统计量F值
# 1.计算组内均值和总体均值
data['组内均值'] = data['满意度'].apply(lambda x:sum(x)/len(x))
data['总体均值'] = data['组内均值'].mean()
print(data)

'''
    行业               满意度           组内均值  总体均值
0  零售业  [57, 66, 49, 40, 34, 53, 44]  49.0  47.75
1  旅游业      [68, 39, 29, 45, 56, 51]  48.0  47.75
2   航空          [31, 49, 21, 34, 40]  35.0  47.75
3  制造业          [44, 51, 65, 77, 58]  59.0  47.75
'''

$$\begin{array}{l}2.计算各误差平方差\\ 组内平方差:\\ SSE={\sum }_{i=1}^k{\sum }_{j=1}^{n_i}(x_{ij}-\overline{x_i})\\ =(57-49{)}^2+...+(68-48{)}^2+...+(31-35{)}^2+...+(44-59{)}^2+...+(58-59{)}^2=2708\\ 注：k:行业类别数;n_i：第i行业样本量\\ 组间平方差：\\ SSA={\sum }_{i=1}^k{n}_i(\overline{x_i}-\overline{\overline{x}})\\ =7\ast (49-47.75{)}^2+6\ast (48-47.75{)}^2+5\ast (35-47.74{)}^2+5\ast (59-47.75{)}^2=1455.66\\ \\ 3.计算统计量F\\ F=\frac{SSA/(k-1)}{SSE/(n-k)}=\frac{1455.66/3}{2708/19}=3.4\\ k-1:组间误差自由度；n-k：组内误差自由度\\ \\ 4.查验临界值表\\ F_{0.05}(3,19)=3.13;3.4>3.13；\\ 拒绝0假设，相信总体均值之间存在差异\end{array}$$

2.1 使用方差分析（F检验）进行特征筛选

## 使用方差分析（F检验）进行特征筛选
# sklearn中 F检验用来捕捉每个特征与标签之间的线性关系的方法，可做分类，也可回归
# F检验在数据服从正态分布时效果稳定，使用F检验过滤特征，最好将数据转化为服从正态分布。

from sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import f_classif,f_regression,chi2,mutual_info_regression,mutual_info_classif,SelectKBest
from sklearn.metrics import accuracy_score

# 测试F检验进行特征过滤
data = load_digits()
X = data.data
y = data.target
print(X.shape)

# 数据集拆分
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)

# 1. 不进行特征筛选，进行模型训练
rf = RandomForestClassifier()
rf.fit(x_train,y_train)
print(f'不进行特征过滤,测试集正确率：{accuracy_score(y_true=y_test,y_pred=rf.predict(x_test))}')

'不进行特征过滤,测试集正确率：0.9777777777777777'

# 使用F检验进行特征筛选从64特征选取Top10，进行模型训练
F_select = SelectKBest(score_func=f_classif,k=32)
x_selected_train = F_select.fit_transform(x_train,y_train)
x_selected_test = F_select.transform(x_test)
rf = RandomForestClassifier()
rf.fit(x_selected_train,y_train)
print(f'F检验选取50%特征,测试集正确率：{accuracy_score(y_true=y_test,y_pred=rf.predict(x_selected_test))}')

'F检验选取50%特征,测试集正确率：0.975'

# 数据集特征数从64减至32个，减少一半，测试集只下降0.2%

3、卡方检验（用于特征筛选、卡方分箱）

目的：主要研究分类变量与各分类变量下样本构成比的关联情况。根本思想：比较真实频数与理论频数差异

eg: 性别变量对是否违约有影响。

真实频数分布：

是否违约 男 女 合计

​ 是 120 80 200

​ 否 200 220 420

​ 合计 320 300 620

理论频数分布：

H0假设：性别对是否违约无影响。

总体违约率: 200/620=32.25%

男性违约期望值320*32.25%=104，非违约期望值 320-104=216

女性违约期望值300*32.25%=97，非违约期望值 300-97=203

是否违约 男 女 合计

​ 是 104 97 200

​ 否 216 203 420

​ 合计 320 300 620
$$\begin{array}{l}卡方值{\chi }^2=\frac{(120-104{)}^2}{104}+\frac{(200-216{)}^2}{216}+\frac{(80-97{)}^2}{97}+\frac{(220-203{)}^2}{203}=8.05\\ 根据显著性水平a=0.05和自由度(2-1)\ast (2-1)=1查询临界值为3.841，\\ 8>>3.8，拒绝原假设，性别对是否违约有影响。\end{array}$$

3.1 逻辑回归之卡方分箱：

## 使用卡方进行连续值分箱操作
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score,precision_score,recall_score,RocCurveDisplay

import pandas as pd
import numpy as np
import scipy
import matplotlib.pyplot as plt

# woe编码和IV值(卡方分箱),适合逻辑回归
# 创建分箱数据(购买保险客户年龄主要集中在20~40岁，以此创建年龄与购买产品可能性)
labels = np.hstack([np.random.choice(a=[0,1],size=20,p=[0.9,0.1]),
                    np.random.choice(a=[0,1],size=20,p=[0.2,0.8]),
                    np.random.choice(a=[0,1],size=60,p=[0.9,0.1])])
            
data = pd.DataFrame({'age':range(100),'购买客户':labels})

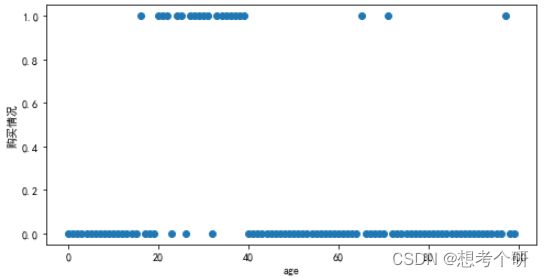
# 绘制购买情况随年龄变化分布
fig = plt.figure(figsize=(8,4))
plt.scatter(data['age'],data['购买客户'])
plt.xlabel('age')
plt.ylabel('购买情况')

从购买分布图可以看出：购买客户主要集中在20~40岁,
age字段分箱理论为0-20,21-40,41-99三个分箱数或21-40,0-20+41-99两个分箱数最佳

# 利用卡方检验进行分箱,对卡方值小的两箱，进行合箱，直到减少至指定箱数
class CHI2_CUT:
    def __init__(self,target_bin_num,init_bin_num=20,correction=0.1):
        self.target_bin_num = target_bin_num  # 目标分箱数
        self.init_bin_num = init_bin_num  # 初始分箱数(等频分箱)
        self.correction = correction  # 样本为空，修正系数 
        
    def fit(self,X,label):
        # 粗粒度分箱,采用等频分箱20组,记录分箱数据上下限
        bins = pd.qcut(X,q=self.init_bin_num,labels=range(self.init_bin_num),retbins=True)
        self.bin_range = dict([(i,[bins[1][i],bins[1][i+1]])for i in bins[0].unique()])
    
        # 统计各分箱内正负标签比例
        data_ = pd.DataFrame({'bins':bins[0],'label':label})
        bin_data_1 = data_.groupby(by=['bins','label'])['label'].count()
        bin_data_2 = pd.pivot(data=bin_data_1.reset_index(name='count'),index='bins',columns='label',values='count')
        self.bin_data_dict = dict(zip(bin_data_2.index,bin_data_2.values.tolist()))
    
        # 分箱合并。直到等于指定分箱数
        while len(self.bin_range) > self.target_bin_num:
            # 两两分箱间进行卡方检验，计算卡方值
            bin_chi2 = []
            for i in range(len(self.bin_data_dict)-1):
                num = list(self.bin_data_dict.keys())[i]
                next_num = list(self.bin_data_dict.keys())[i+1]
                # 对箱内正负样本某项为0的进行修正
                bin_chi2_1_and_2 = [[i+self.correction for i in self.bin_data_dict.get(num)],
                                   [i+self.correction for i in self.bin_data_dict.get(next_num)]]
            
                bin_chi2.append(scipy.stats.chi2_contingency(bin_chi2_1_and_2)[0])
    
            # 选取卡方值最小的两箱进行合并，更新合并箱的分割点和箱内正负样本比例
            index = bin_chi2.index(min(bin_chi2))
            bin_index = list(self.bin_range.keys())[index]
            bin_index_concat = list(self.bin_range.keys())[index+1]  
        
            # 合箱，更新分箱数据分割点
            self.bin_range.get(bin_index)[1] = self.bin_range.get(bin_index_concat)[1] # 更新合箱后数据分割点
            self.bin_range.pop(bin_index_concat) # 删除被合并的分箱
        
            # 更新合箱后样本比例
            self.bin_data_dict.get(bin_index)[0] += self.bin_data_dict.get(bin_index_concat)[0]
            self.bin_data_dict.get(bin_index)[1] += self.bin_data_dict.get(bin_index_concat)[1]
            self.bin_data_dict.pop(bin_index_concat)
            
    def transform(self,X):
        # 利用卡方合并分箱后的分割点上下限，对连续数据进行编码，并计算WOE值
        negative_sample_num = np.sum(np.array(list(self.bin_data_dict.values())),axis=0)[0]
        positive_sample_num = np.sum(np.array(list(self.bin_data_dict.values())),axis=0)[1]
        self.bin_woe = {}
        for i in self.bin_data_dict:
            p_rate = (self.bin_data_dict[i][1]+self.correction)/positive_sample_num
            n_rate = (self.bin_data_dict[i][0]+self.correction)/negative_sample_num
            self.bin_woe[i] = np.log(p_rate/n_rate)
        
        # 对数据特征重新进行编码映射
        x = X.apply(lambda x:self._f(x))          
        x = x.apply(lambda x:self.bin_woe.get(x))            
        return x
    
    def _f(self,x):
        for index,value in self.bin_range.items():
                if x>=value[0] and x<= value[1]:
                    return index

                
## 进行卡方分箱和不进行卡方分箱效果对比
# 不进行分箱，直接使用逻辑回归训练
lr_without_bin = LogisticRegression()
lr_without_bin.fit(data[['age']],data['购买客户'])
print(f"正确率：{accuracy_score(data['购买客户'],lr_without_bin.predict(data[['age']]))}")
print(f"精准率：{precision_score(data['购买客户'],lr_without_bin.predict(data[['age']]),pos_label=1)}")
print(f"召回率：{recall_score(data['购买客户'],lr_without_bin.predict(data[['age']]),pos_label=1)}")
RocCurveDisplay.from_estimator(estimator=lr_without_bin,X=data[['age']],y=data['购买客户'],pos_label=1)


# 利用卡方分箱对数据进行woe编码
chi2_cut = CHI2_CUT(target_bin_num=5)
chi2_cut.fit(data['age'],data['购买客户'])
data['chi2_cut'] = chi2_cut.transform(data['age'])

lr_with_chi2 = LogisticRegression()
lr_with_chi2.fit(data[['age','chi2_cut']],data['购买客户'])
print(f"正确率：{accuracy_score(data['购买客户'],lr_with_chi2.predict(data[['age','chi2_cut']]))}")
print(f"精准率：{precision_score(data['购买客户'],lr_with_chi2.predict(data[['age','chi2_cut']]),pos_label=1)}")
print(f"召回率：{recall_score(data['购买客户'],lr_with_chi2.predict(data[['age','chi2_cut']]),pos_label=1)}")
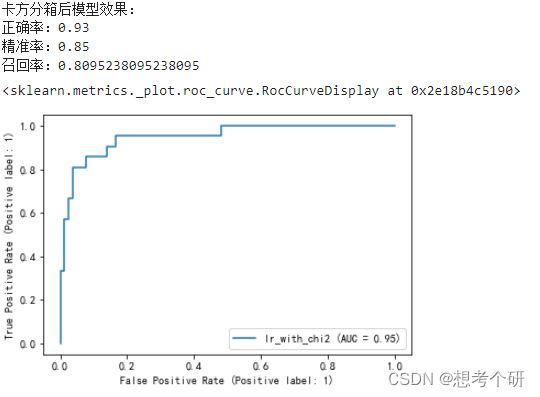
RocCurveDisplay.from_estimator(estimator=lr_with_chi2,X=data[['age','chi2_cut']],y=data['购买客户'],pos_label=1)

不进行卡方分箱模型效果：

卡方分箱后模型效果：

注意：这里卡方分箱没有使用IV值进行最佳分箱数的选取

4、互信息法（用于特征筛选）

$$\begin{array}{l}H(X),H(Y)表示事件X、Y的信息熵\\ H(X|Y)、H(Y|X):条件熵，表示知道事件X情况，再知道事件Y可以带来多少信息\\ I(X;Y):互信息，表示事件X、Y共同提供的信息；也可理解为知道事件X可以对事件Y提供多少信息，反之亦然。\end{array}$$

4.1 使用互信息法进行特征筛选

## 2. 互信息法
from sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import f_classif,f_regression,chi2,mutual_info_regression,mutual_info_classif,SelectKBest
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 测试互信息进行特征过滤
data = load_digits()
X = data.data
y = data.target
print(X.shape) # (1797, 64)

# 数据集拆分
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)

# 不进行特征筛选，进行模型训练
rf = RandomForestClassifier()
rf.fit(x_train,y_train)
print(f'不进行特征过滤,测试集正确率：{accuracy_score(y_true=y_test,y_pred=rf.predict(x_test))}')

# 使用F检验进行特征筛选从64特征选取Top10，进行模型训练
F_select = SelectKBest(score_func=mutual_info_classif,k=32)
x_selected_train = F_select.fit_transform(x_train,y_train)
x_selected_test = F_select.transform(x_test)
rf = RandomForestClassifier()
rf.fit(x_selected_train,y_train)
print(f'利用互信息法选取50%特征,测试集正确率：{accuracy_score(y_true=y_test,y_pred=rf.predict(x_selected_test))}')

'''
不进行特征过滤,测试集正确率：0.975
利用互信息法选取50%特征,测试集正确率：0.972222222222222
'''

---

统计原理参考：

参考博客：https://zhuanlan.zhihu.com/p/520252720（T检验）

参考博客：https://blog.csdn.net/olizxq/article/details/99177262（单因素方差分析F检验）

参考博客：https://zhuanlan.zhihu.com/p/94074441（互信息法）