8月5日Pytorch笔记——AutoEncoder、VAE
文章目录
- 前言
- 一、AutoEncoder
-
- 1、Loss function for binary inputs
- 2、Sample() is not differentiable
- 二、Variational Autoencoders
前言
本文为8月5日Pytorch笔记,分为两个章节:
- AutoEncoder;
- Variational Autoencoders。
一、AutoEncoder
1、Loss function for binary inputs
l ( f ( x ) ) = ∑ k ( x k l o g ( x ^ k ) + ( 1 − x k ) l o g ( 1 − x ^ k ) ) l(f(x)) = {\textstyle \sum_{k}} (x_klog(\hat{x}_k ) + (1 - x_k)log(1 - \hat{x}_k)) l(f(x))=∑k(xklog(x^k)+(1−xk)log(1−x^k))
-
Loss function for real-valued inputs:
l ( f ( x ) ) = 1 2 ∑ k ( x ^ k − x k ) 2 l(f(x)) = \frac{1}{2} {\textstyle \sum_{k}} (\hat{x}_k - x_k)^2 l(f(x))=21∑k(x^k−xk)2 -
KL between q ( z ) q(z) q(z) and p ( z ) p(z) p(z):
p ( z i ) ∈ N ( μ 1 , σ 1 2 ) q ( z i ) ∈ N ( μ 2 , σ 2 2 ) K L ( p , q ) = − ∫ p ( x ) l o g q ( x ) d x + ∫ p ( x ) l o g p ( x ) d x = l o g σ 2 σ 1 + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 p(z_i) \in N(\mu_1, \sigma_1^2)\\ q(z_i) \in N(\mu_2, \sigma_2^2)\\ KL(p, q) = -\int p(x)logq(x)dx + \int p(x)logp(x)dx\\ =log\frac{\sigma_2}{\sigma_1} + \frac{\sigma _1^2 + (\mu_1 - \mu _2)^2}{2\sigma _2^2} - \frac{1}{2} p(zi)∈N(μ1,σ12)q(zi)∈N(μ2,σ22)KL(p,q)=−∫p(x)logq(x)dx+∫p(x)logp(x)dx=logσ1σ2+2σ22σ12+(μ1−μ2)2−21
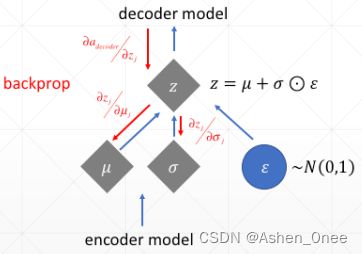
2、Sample() is not differentiable
import torch
from torch import nn
class AE(nn.Module):
def __init__(self):
super(AE, self).__init__()
# [b, 784]
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 20),
nn.ReLU()
)
# [b, 20]
self.decoder = nn.Sequential(
nn.Linear(20, 64),
nn.ReLU(),
nn.Linear(64, 256),
nn.ReLU(),
nn.Linear(256, 784),
nn.Sigmoid()
)
def forward(self, x):
'''
:param x: [b, 1, 28, 28]
:return:
'''
batchsz = x.size(0)
# flatten
x = x.view(batchsz, 784)
# encoder
x = self.encoder(x)
# decoder
x = self.decoder(x)
# reshape
x = x.view(batchsz, 1, 28, 28)
return x
二、Variational Autoencoders
代码如下:
- VAE:
import numpy as np
import torch
from torch import nn
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
# [b, 784]
# \mu: [b, 10]
# \sigma: [b, 10]
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 20),
nn.ReLU()
)
# [b, 20]
self.decoder = nn.Sequential(
nn.Linear(10, 64),
nn.ReLU(),
nn.Linear(64, 256),
nn.ReLU(),
nn.Linear(256, 784),
nn.Sigmoid()
)
def forward(self, x):
'''
:param x: [b, 1, 28, 28]
:return:
'''
batchsz = x.size(0)
# flatten
x = x.view(batchsz, 784)
# encoder
# [b, 20], including mean and \sigma
h_ = self.encoder(x)
# [b, 20] ==> [b, 10] and [b, 10]
mu, sigma = h_.chunk(2, dim=1)
# reparametrize tirck, epsilon~N(0, 1)
h = mu + sigma * torch.rand_like(sigma)
# decoder
x_hat = self.decoder(h)
# reshape
x_hat = x_hat.view(batchsz, 1, 28, 28)
# KL divergence
kld = 0.5 * torch.sum(
torch.pow(mu, 2) +
torch.pow(sigma, 2) -
torch.log(1e-8 + torch.pow(sigma, 2)) - 1
) / (batchsz * 28 * 28)
return x_hat, kld
- main:
import torch
from torch.utils.data import DataLoader
from torch import nn, optim
from torchvision import transforms, datasets
from test_autoencoder import AE
from test_vae import VAE
import visdom
def main():
mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)
mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)
x, _ = iter(mnist_train).next()
print('x:', x.shape)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# model = AE().to(device)
model = VAE().to(device)
criteon = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
print(model)
viz = visdom.Visdom()
for epoch in range(1000):
for batchidx, (x, _) in enumerate(mnist_train):
# [b, 1, 28, 28]
x = x.to(device)
x_hat, kld = model(x)
loss = criteon(x_hat, x)
if kld is not None:
elbo = - loss - 1.0 * kld
loss = - elbo
# backprop
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(epoch, 'loss:', loss.item(), 'kld:', kld.item())
x, _ = iter(mnist_test).next()
x = x.to(device)
with torch.no_grad():
x_hat, kld = model(x)
viz.images(x, nrow=8, win='x', opts=dict(title='x'))
viz.images(x_hat, nrow=8, win='x_hat', opts=dict(title='x_hat'))
if __name__ == '__main__':
main()
- 运行结果:
>>> 41 loss: 0.027249876409769058 kld: 0.006576840300112963