GNN动手实践(一):手把手带你实现GCN
参考论文:Semi-Supervised Classification with Graph Convolutional Networks
一.前言
GCN(Graph Convolutional Network)即在图上进行卷积运算,与传统卷积的操作对象不同,GCN的卷积对象图是不规则的,例如每个结点周围的邻居结点数都是不定的。此外,图中各结点间不是互相独立的。图卷积通常需要借助图的结构信息来指导图中的消息聚合。GCN经过多年来的发展有了很多变体,今天要介绍的是Thomas N.Kipf和Max Welling提出的半监督(semi-supervised)学习模型Semi-GCN,该模型可以用来进行结点预测(Node Classification),话不多说,请看下文!
二.模型简介
首先强调一点,作者提出的GCN模型有效的前提是图是同构的。
在该前提下,我们再来看他们的模型,先给出符号表如下:
| 符号 | 说明 |
|---|---|
| G = { V , E } \mathcal{G} = \{\mathcal{V},\mathcal{E}\} G={V,E} | 无向图,其中 V \mathcal{V} V表示图的点集, E \mathcal{E} E表示图的边集 |
| A ∈ R N × N A \in \mathbb{R}^{N \times N} A∈RN×N | 邻接矩阵,其中 N N N为结点数 |
| D D D | 度矩阵, D i i = ∑ j A i j D_{ii} = \sum_{j}{A_{ij}} Dii=∑jAij |
| X X X | 特征矩阵 |
| H ( l ) H^{(l)} H(l) | 模型第 l + 1 l + 1 l+1层的输入, H ( 0 ) = X H^{(0)}=X H(0)=X |
| W ( l ) W^{(l)} W(l) | 第 l l l层的权重矩阵 |
| A ~ \tilde{A} A~ | A ~ = A + I N \tilde{A} = A + I_N A~=A+IN,表示邻接矩阵加上一个与其size相同的单位阵 |
| D ~ \tilde{D} D~ | D ~ = ∑ j A ~ i j \tilde{D} = \sum_{j}{\tilde{A}_{ij}} D~=∑jA~ij |
| σ \sigma σ | 激活函数 ReLU \text{ReLU} ReLU |
对于一个GNN模型,我们一般比较关注的是它是如何进行消息(message)传播以及消息是如何聚合(Aggerate)的。先来看作者定义的卷积公式:
H ( l + 1 ) = σ ( D ~ − 1 / 2 A ~ D ~ − 1 / 2 H ( l ) W ( l ) ) (1) H^{(l+1)}=\sigma{(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)})} \tag{1} H(l+1)=σ(D~−1/2A~D~−1/2H(l)W(l))(1)
其中 A ~ \tilde{A} A~的含义相当于在图中为每个结点增加自环,如此一来消息聚合时不仅能聚合来自其他结点的消息,还能聚合结点自身的消息。
而 D ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} D~−1/2A~D~−1/2实际就是对 A ~ \tilde{A} A~进行规范化,对于 A ~ \tilde{A} A~中的某个元素 A ~ i j \tilde{A}_{ij} A~ij,其规范化的计算公式为:
Normalization ( A ~ i j ) = A ~ i j D ~ j j D ~ i i (2) \text{Normalization}(\tilde{A}_{ij}) = \frac{\tilde{A}_{ij}}{\sqrt{\tilde{D}_{jj}}\sqrt{\tilde{D}_{ii}}} \tag{2} Normalization(A~ij)=D~jjD~iiA~ij(2)
实际上公式(1)可以表述为下列形式:
h i ( l + 1 ) = σ ( b ( l ) + ∑ j ∈ N ( i ) 1 c j i h j ( l ) W ( l ) ) (3) h_i^{(l+1)} = \sigma(b^{(l)} + \sum_{j\in\mathcal{N}(i)}\frac{1}{c_{ji}}h_j^{(l)}W^{(l)}) \tag{3} hi(l+1)=σ(b(l)+j∈N(i)∑cji1hj(l)W(l))(3)
其中 h i ( l + 1 ) h_i^{(l+1)} hi(l+1)表示图中第 i i i个结点第 l + 1 l+1 l+1次消息传递聚合的消息, N ( i ) \mathcal{N}(i) N(i)是结点 i i i的邻居的集合, c j i = D ~ j j D ~ i i c_{ji}=\sqrt{\tilde{D}_{jj}}\sqrt{\tilde{D}_{ii}} cji=D~jjD~ii。可以将其表述为Message + Aggerate的形式,即:
最后摆出模型的前向传播公式:
Z = f ( X , A ) = softmax ( A ^ ReLU ( A ^ X W ( 0 ) ) W ( 1 ) ) (4) Z = f(X,A) = \text{softmax}(\hat{A} \ \text{ReLU}(\hat{A}XW^{(0)})W^{(1)}) \tag{4} Z=f(X,A)=softmax(A^ ReLU(A^XW(0))W(1))(4)
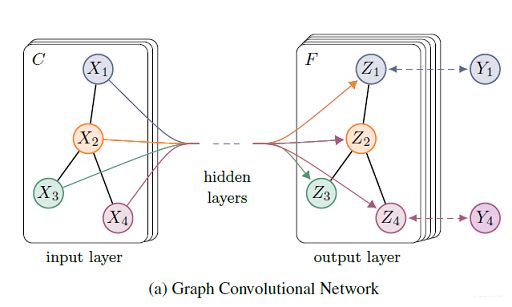
从公式(4)我们可以看出该模型实际是两个卷积层+SoftMax构成的,作者将其模型可视化为:
三.具体复现
模型的实现采用的是Pytorch + DGL,其中DGL是方便图神经网络实现的Python库。DGL库的具体使用请自行查看相应的教程,限于篇幅原因,就不详细介绍了。
3.1 GCN层的实现
先给出GCN层的实现代码:
class GCNLayer(nn.Module):
def __init__(self,in_feats,out_feats,bias=True):
super(GCNLayer,self).__init__()
self.weight = nn.Parameter(torch.Tensor(in_feats,out_feats))
if bias:
self.bias = nn.Parameter(torch.zeros(out_feats))
else:
self.bias = None
self.reset_parameter()
def reset_parameter(self):
nn.init.xavier_uniform_(self.weight)
def forward(self,g,h):
with g.local_scope():
h = torch.matmul(h,self.weight)
g.ndata['h'] = g.ndata['norm'] * h
g.update_all(message_func = fn.copy_u('h','m'),
reduce_func=fn.sum('m','h'))
h = g.ndata['h']
h = h * g.ndata['norm']
if self.bias is not None:
h = h + self.bias
return h
其中g.ndata['norm']就是 D ~ − 1 / 2 \tilde{D}^{-1/2} D~−1/2,其实现源码为:
# 获取度矩阵 D
degs = g.out_degrees().float()
# 计算D^{-1/2}
norm = torch.pow(degs, -0.5)
# inf的值表示该处原来的值为0
norm[torch.isinf(norm)] = 0
g.ndata['norm'] = norm.unsqueeze(1)
在DGL中我们只需要定义好消息函数message_func和聚合函数reduce_func,然后调用update_all函数就能完成消息的传递和聚合。
3.2 基于GCN层的模型实现
基于3.1节实现的GCN层,我们就可以定义任意层数GCN的模型,下面给出使用两层GCN的模型源码:
class GCNModel(nn.Module):
def __init__(self,in_feats,h_feats,num_classes,bias=True):
super(GCNModel,self).__init__()
self.conv1 = GCNLayer(in_feats,h_feats,bias)
self.conv2 = GCNLayer(h_feats,num_classes,bias)
def forward(self,g,in_feat):
h = self.conv1(g,in_feat)
h = F.relu(h)
h = self.conv2(g,h)
return h
四.复现模型上的实验
基于复现的GCNModel模型,我使用作者实验中用到的Cora数据集来进行训练与测评。
4.1 数据集简介
Cora是一个论文引用网络数据集,其中包含了2708篇论文,每篇论文都由1433维的词向量表示,词向量的每个元素只能取0或1,0表示论文中包含该词,1表示论文中不包含该词。Cora数据集中的论文被分为7种类型:Case_Based、Theory、Genetic_Algorithms、 Neural_Networks、Probabilistic_Methods、Reinforcement_Learning、Rule_Learning。
DGL库中实际就已经包含了该数据集,通过dgl.data.CoraGraphDataset我们就能够下载和导入该数据集:
dataset = dgl.data.CoraGraphDataset(raw_dir="../Datasets/")
g = dataset[0]
"""
NumNodes: 2708
NumEdges: 10556
NumFeats: 1433
NumClasses: 7
NumTrainingSamples: 140
NumValidationSamples: 500
NumTestSamples: 1000
"""
从上述信息可以看出,DGL还把数据集分为训练集、验证集和测试集。
4.2 实验结果展示
由于时间原因,实验的过程中并未完全参照论文中的做法,本次实验的配置如下:
| Item | Configuration |
|---|---|
| optimizer | Adam |
| epochs | 200 |
| hidden_size | 32 |
| lr | 0.01 |
| weight_decay | 5e-4 |
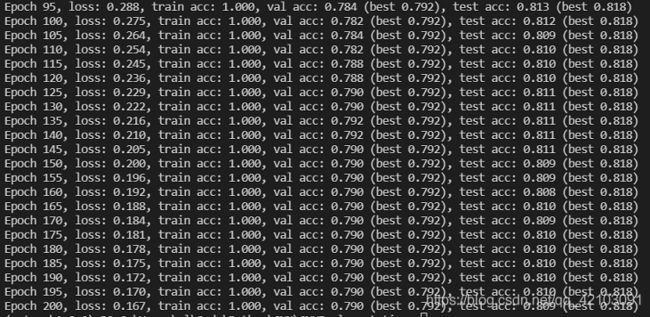
其所对应的训练集、验证集与测试集的准确率变化曲线如下:

可以看出复现模型的性能还是不错的,基本与论文中在该数据集上的结果差不多。
五.结语
源码开源地址:Semi-GCN
以上便是本文的全部内容,要是觉得不错的话就点个赞或关注一下博主吧,你们的支持是博主继续创作的不解动力,当然若是有任何问题也敬请批评指正!!!