Python和Java代码实现：黄金分割法求解一维最优化问题

问题描述

我不是运筹学科班出身，工作之前只做过梯度优化算法和智能优化算法在航天场景中的改进和应用。毕业后虽然选择了运筹优化算法工程师的道路，但却深知自己的运筹认知不够体系化，很想找些书，系统补一下这方面的基础内容。

不过现在国内的运筹学教材大多都是单纯形法起步，看起来挺费劲的。而且我的关注点有：算法原理、不同算法间的联系和区别、工程（Python/Java）实现等，很多内容书上也很难都有。
所以我打算基于一些比较简单的优化问题为起点，从简单到复杂，自行去认识和理解这些运筹优化算法。

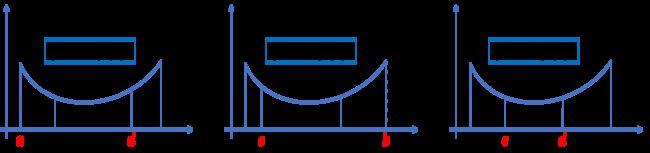
能想到的最简单的优化问题，应该就是一维最优化问题了：在一个搜索区间内，包含了目标函数的极小值点，而且是个单峰区间，即在该区间内目标函数只有一个极值，下图为一维最优化问题的示意图。

区间消去法

为了解决以上的一维最优化问题，一种朴素的方法是区间消去法：我们在区间$[a,b]$内取两个点$c,d$，其中$a<c<d<b$，并计算对应的目标函数$f(c),f(d)$，可能会出现以下三种情况：

(1) $f(c)<f(d)$。因为函数是单峰的，所以极小值必位于点$d$的左侧，搜索区间可以缩小为$[a,d]$。

(2) $f(c)>f(d)$。极小值位于点$c$的右侧，搜索区间可以缩小为$[c,b]$。

(3) $f(c)=f(d)$。极小值位于点$c$和点$d$之间，搜索区间缩小为$[c,d]$。

按照以上逻辑不断选取两个点做对比，便可以不断缩小搜索区间，直至搜索区间的长度低于某阈值，即找到了极小值。

事实上，以上三种情况还可以简化为两种：

(1) 如果$f(c)<f(d),则搜索区间[a,b]$缩小为$[a,d]$。

(2) 如果$f(c)\ge f(d),则搜索区间[a,b]$缩小为$[c,b]$。

黄金分割法

区间消去法虽然给出了搜索区间缩小的原理，但是每次$c$和$d$该如何选择，却并没有给出具体方案。黄金分割法便在区间消去法的基础上，对c和d的选择做了约束，进而给出它们的确定逻辑：

(1) $c-a=b-d$，即点a到点c的距离等于点d到点b的距离。

(2) 保留的区间长度$l$与原区间长度$L$之比等于被消去的区间长度$(L-l)$与保留区间长度$l$之比，即
$$\frac{l}{L}=\frac{L-l}{l}$$
其中
$$l=d-a,L=b-a,L-l=b-d$$
令
$$\lambda =\frac{l}{L}$$
第一个等式变为
$${\lambda }^2+\lambda -1=0$$
求解可得
$$\lambda =0.618$$
因此
$$d-a=0.618(b-a),b-d=0.382(b-a)$$

代码实现

本文会基于Python和Java语言进行算法实现。Python代码简单，便于学习理解；Java运行速度快，便于工程应用；MATLAB版本就不考虑了，对运筹优化算法的学习和落地应用而言,MATLAB基本没有多少竞争力。

本文待优化的一维最优化问题为
$$min(t^2-5t+8)$$
该问题最小值为1.75，其对应的$t=2.5$。

Python代码

以下的golden_section函数为黄金分割法的Python代码。除该代码外，主函数中还增加了一个for循环，该循环的目的是多次重复调用黄金分割法，以此评估Python代码的计算耗时。

import time


# 待优化函数
def f(t):
    return t ** 2 - t * 5 + 8


def golden_section(a, b, eps):
    # 统计迭代次数
    cnt = 0
    while b - a > eps:
        # 根据黄金分割法规则选择内部两点
        c = a + (b - a) * 0.382
        d = a + (b - a) * 0.618

        # 区间消去原理
        if f(c) < f(d):
            b = d
        else:
            a = c

        cnt += 1

    # 两点的中点定义为最优解
    return (a + b) / 2, f((a + b) / 2), cnt


if __name__ == '__main__':
    # 参数设置
    left_point = 1
    right_point = 7
    min_interval_value = 0.1

    # 调用黄金分割法函数求解最小值
    best_x, best_y, iter_cnt = 0, 0, 0
    t0 = time.time()
    for i in range(100000):
        best_x, best_y, iter_cnt = golden_section(left_point, right_point, min_interval_value)
    print('总耗时为：{} ms'.format((time.time() - t0) * 1000))
    print('best_x: {}, best_y: {}, iter_cnt: {}.'.format(best_x, best_y, iter_cnt))

Java代码

以下的goldenSection函数为黄金分割法的Java代码。与上文一样，主函数中也增加了一个for循环，以此评估Java代码的计算耗时。

public class GoldenSection {

    // 主函数入口
    public static void main(String[] args) {
        // 参数设置
        int leftPoint = 1;
        int rightPoint = 7;
        double minIntervalValue = 0.1;

        long t0 = System.currentTimeMillis();
        Solution best_solution = new Solution();
        for (int i = 0; i < 100000; i++) {
            // 调用黄金分割法函数求解最小值
             best_solution = goldenSection(leftPoint, rightPoint, minIntervalValue);
        }
        System.out.println("计算总耗时为: " + (System.currentTimeMillis()-t0) + " ms");
        // 输出优化结果
        System.out.println("best_x: " + best_solution.best_x);
        System.out.println("best_y: " + best_solution.best_y);
        System.out.println("cnt: " + best_solution.cnt);

    }


    // 黄金分割法
    private static Solution goldenSection(double a, double b, double eps) {
        // 统计迭代次数
        int cnt = 0;

        while (b - a > eps) {

            // 根据黄金分割法规则选择内部两点
            double c = a + (b - a) * 0.382;
            double d = a + (b - a) * 0.618;

            // 区间消去原理
            if (f(c) < f(d)) {
                b = d;
            } else {
                a = c;
            }

            // 更新迭代次数
            cnt ++;
        }

        // 构造最优解对象
        Solution best_solution = new Solution();
        best_solution.best_x = (a + b) / 2;
        best_solution.best_y = f((a + b) / 2);
        best_solution.cnt = cnt;

        return best_solution;
    }


    // 待优化函数
    private static double f(double t) {
        return t * t - t * 5 + 8;
    }


    // 解对象
    private static class Solution {
        double best_x;
        double best_y;
        int cnt;
    }
}

求解实例

首先运行Python代码，可以得到最优解为1.75，迭代次数为9次。计算100000次，共耗时515毫秒。

总耗时为：515.2740478515625 ms
best_x: 2.5045211503093046, best_y: 1.7500204408001192, iter_cnt: 9.

再运行Java代码，可以得到和Python代码相同的解。计算100000次，仅耗时11毫秒。相比之下，Java代码耗时仅为Python代码耗时的2%。对运筹优化算法来说，计算速度是非常重要的，所以如果代码能力允许，尽量使用Java。

计算总耗时为: 11 ms
best_x: 2.5045211503093046
best_y: 1.7500204408001192
cnt: 9