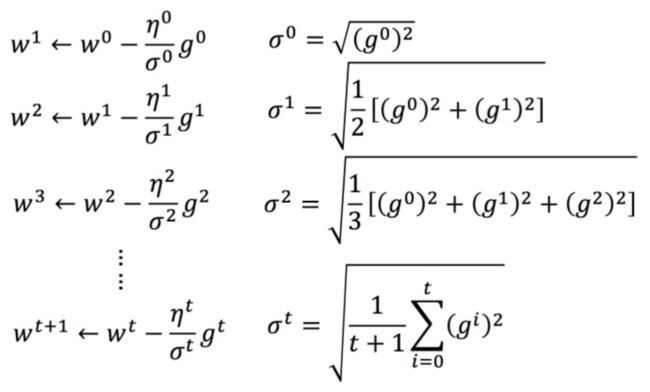【机器学习】梯度下降算法
文章目录
- 参考资料
- 1. 基本概念
-
- 1.1 自适应学习率
- 1.2 Adagrad 算法
- 2. 随机梯度下降法
- 3. 理论基础
-
- 3.1 泰勒展开
- 4. 梯度下降限制
- 5. 梯度检查
参考资料
- LeeML-Notes
- https://www.zybuluo.com/hanbingtao/note/476663
强烈建议阅读一篇英文博客,讲得非常全面清楚。它的相应的中文翻译博客 参考https://blog.csdn.net/google19890102/article/details/69942970
1. 基本概念
在回归问题的第三步中,需要解决下面的最优化问题:
θ ∗ = arg min θ L ( θ ) (1) \theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) \tag1 θ∗=θarg minL(θ)(1)
- L L L :lossfunction(损失函数)
- θ \theta θ :parameters(参数)
这里的parameters是复数,即 θ \theta θ 指代一堆参数,比如上篇说到的 w w w 和 b b b 。
我们要找一组参数 θ \theta θ ,让损失函数越小越好,这个问题可以用梯度下降法解决:

然后分别计算初始点处,两个参数对 L L L 的偏微分,然后 θ 0 \theta^0 θ0 减掉 η \eta η 乘上偏微分的值,得到一组新的参数。同理反复进行这样的计算。 ▽ L ( θ ) \triangledown L(\theta) ▽L(θ) 即为梯度, η \eta η 叫做Learning rates(学习速率)。
1.1 自适应学习率
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
-
通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
-
update好几次参数之后比较靠近最低点了,此时减少学习率
-
比如 η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1ηt, t t t 是次数。随着次数的增加, η t \eta^t ηt 减小
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
1.2 Adagrad 算法
详情可参考知乎。Adagrad 涉及到动量的知识。
每个参数的学习率都把它除上之前微分的均方根。解释:
普通的梯度下降为:
w t + 1 ← w t − η t g t (3) w^{t+1} \leftarrow w^t -η^tg^t \tag3 wt+1←wt−ηtgt(3) η t = η t t + 1 (4) \eta^t =\frac{\eta^t}{\sqrt{t+1}} \tag4 ηt=t+1ηt(4)
w w w 是一个参数
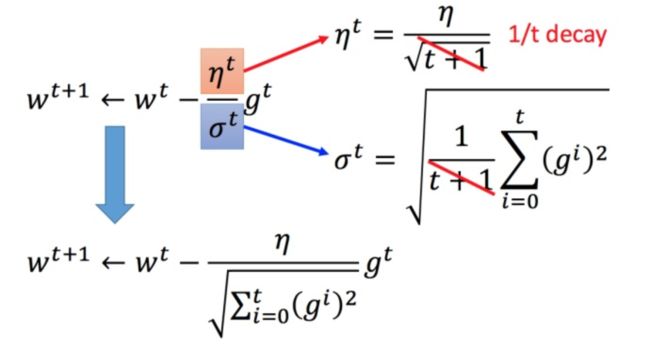
Adagrad 可以做的更好: w t + 1 ← w t − η t σ t g t (5) w^{t+1} \leftarrow w^t -\frac{η^t}{\sigma^t}g^t \tag5 wt+1←wt−σtηtgt(5) g t = ∂ L ( θ t ) ∂ w (6) g^t =\frac{\partial L(\theta^t)}{\partial w} \tag6 gt=∂w∂L(θt)(6)
σ t \sigma^t σt :之前参数的所有微分的均方根,对于每个参数都是不一样的。
2. 随机梯度下降法
原本梯度下降公式为:
L = ∑ n ( y ^ n − ( b + ∑ w i x i n ) ) 2 (8) L=\sum_n(\hat y^n-(b+\sum w_ix_i^n))^2 \tag8 L=n∑(y^n−(b+∑wixin))2(8) θ i = θ i − 1 − η ▽ L ( θ i − 1 ) (9) \theta^i =\theta^{i-1}- \eta\triangledown L(\theta^{i-1}) \tag9 θi=θi−1−η▽L(θi−1)(9)
而随机梯度下降法中,损失函数不需要处理训练集所有的数据,而是随机选取一个数据,如 x n x^n xn
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 (10) L=(\hat y^n-(b+\sum w_ix_i^n))^2 \tag{10} L=(y^n−(b+∑wixin))2(10) θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) (11) \theta^i =\theta^{i-1}- \eta\triangledown L^n(\theta^{i-1}) \tag{11} θi=θi−1−η▽Ln(θi−1)(11)
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数Ln,就可以更新梯度。
常规梯度下降法走一步要处理到所有二十个例子,但随机算法此时已经走了二十步(每处理一个例子就更新)
- 随机也就是说我们随机采用样本中的一个例子来近似我所有的样本,来调整θ,因而随机梯度下降是会带来一定的问题,因为计算得到的并不是准确的一个梯度,对于最优化问题、凸问题,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近
- 随机梯度下降法最终收敛不到最优解,而是会收敛到最优解的附近浮动。
在SGD算法中,每次更新的迭代,只计算一个样本。这样对于一个具有数百万样本的训练数据,完成一次遍历就会对更新数百万次,效率大大提升。由于样本的噪音和随机性,每次更新并不一定按照减少的方向。然而,虽然存在一定随机性,大量的更新总体上沿着减少的方向前进的,因此最后也能收敛到最小值附近。下图展示了SGD(Stochastic Gradient Descent)和BGD(Batch Gradient Descent)的区别。

如上图,椭圆表示的是函数值的等高线,椭圆中心是函数的最小值点。红色是BGD的逼近曲线,而紫色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的,而SGD明显躁动了许多,但总体上仍然是向最低点逼近的。
最后需要说明的是,SGD不仅仅效率高,而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』,沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说,存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值,从而获得一个更好的模型。
3. 理论基础
当用梯度下降解决问题:
θ ∗ = arg min θ L ( θ ) (1) \theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) \tag1 θ∗=θarg minL(θ)(1)
每次更新参数 θ \theta θ,都得到一个新的 θ \theta θ,它都使得损失函数更小。即:
L ( θ 0 ) > L ( θ 1 ) > L ( θ 2 ) > ⋅ ⋅ ⋅ (13) L(\theta^0) >L(\theta^1)>L(\theta^2)>···\tag{13} L(θ0)>L(θ1)>L(θ2)>⋅⋅⋅(13)
上述结论正确吗?
结论是不正确的。
比如在 θ 0 \theta^0 θ0 处,可以在一个小范围的圆圈内找到损失函数细小的 θ 1 \theta^1 θ1,不断的这样去寻找。

接下来就是如何在小圆圈内快速的找到最小值?
3.1 泰勒展开
定义
若 h ( x ) h(x) h(x) 在 x = x 0 x=x_0 x=x0 点的某个领域内有无限阶导数(即无限可微分,infinitely differentiable),那么在此领域内有:
h ( x ) = ∑ k = 0 ∞ h k ( x 0 ) k ! ( x − x 0 ) k = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ (14) \begin{aligned} h(x) &= \sum_{k=0}^{\infty }\frac{h^k(x_0)}{k!}(x-x_0)^k \ & =h(x_0)+{h}'(x_0)(x−x_0)+\frac{h''(x_0)}{2!}(x−x_0)^2+⋯ \tag{14} \end{aligned} h(x)=k=0∑∞k!hk(x0)(x−x0)k =h(x0)+h′(x0)(x−x0)+2!h′′(x0)(x−x0)2+⋯(14)
当 x x x 很接近 x 0 x_0 x0 时,有 h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)≈h(x_0)+{h}'(x_0)(x−x_0) h(x)≈h(x0)+h′(x0)(x−x0) 式14 就是函数 h ( x ) h(x) h(x) 在 x = x 0 x=x_0 x=x0 点附近关于 x x x 的幂函数展开式,也叫泰勒展开式。
多变量泰勒展开式
利用泰勒展开式简化
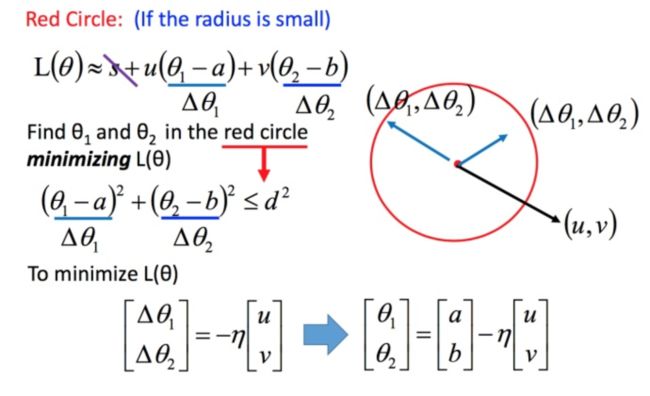
回到之前如何快速在圆圈内找到最小值。基于泰勒展开式,在 ( a , b ) (a,b) (a,b) 点的红色圆圈范围内,可以将损失函数用泰勒展开式进行简化:
将问题进而简化为下图:
不考虑s的话,可以看出剩下的部分就是两个向量 ( △ θ 1 , △ θ 2 ) (\triangle \theta_1,\triangle \theta_2) (△θ1,△θ2) 和 ( u , v ) (u,v) (u,v) 的内积,那怎样让它最小,就是和向量 ( u , v ) (u,v) (u,v) 方向相反的向量
然后将u和v带入。
L ( θ ) ≈ s + u ( θ 1 − a ) + v ( θ 2 − b ) (14) L(\theta)\approx s+u(\theta_1 - a)+v(\theta_2 - b) \tag{14} L(θ)≈s+u(θ1−a)+v(θ2−b)(14)
发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圈圈足够小(也就是学习率足够小)来保证。所以理论上每次更新参数都想要损失函数减小的话,即保证式1-2 成立的话,就需要学习率足够足够小才可以。
所以实际中,当更新参数的时候,如果学习率没有设好,是有可能式1-2是不成立的,所以导致做梯度下降的时候,损失函数没有越来越小。
式1-2只考虑了泰勒展开式的一次项,如果考虑到二次项(比如牛顿法),在实际中不是特别好,会涉及到二次微分等,多很多的运算。
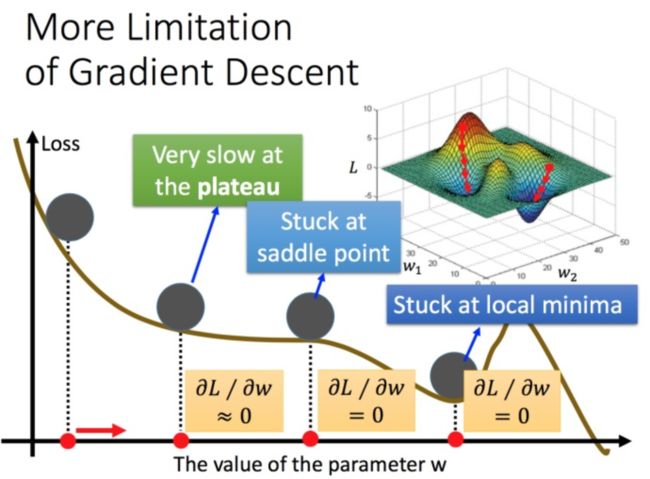
4. 梯度下降限制
容易陷入局部极值 还有可能卡在不是极值,但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点。
5. 梯度检查
对于自己手写实现的神经网络,怎么保证自己写的神经网络没有BUG呢?
利用梯度检查来确认程序是否正确。梯度检查的思路如下:
对于梯度下降算法:
![]()
来说,这里关键之处在于 ∂ E d ∂ ω j i \frac{\partial E_d}{\partial \omega_{ji}} ∂ωji∂Ed的计算一定要正确,而它是 E d E_d Ed对 w j i w_{ji} wji的偏导数。而根据导数的定义:
![]()
对于任意 θ \theta θ的导数值,我们都可以用等式右边来近似计算。我们把 E d E_d Ed看做是 w j i w_{ji} wji的函数,即 E d ( ω j i ) E_d(\omega_{ji}) Ed(ωji),那么根据导数定义, ∂ E d ∂ ω j i \frac{\partial E_d}{\partial \omega_{ji}} ∂ωji∂Ed应该等于:
![]()
如果把 ϵ \epsilon ϵ设置为一个很小的数(比如 1 0 − 4 10^{-4} 10−4),那么上式可以写成:
我们就可以利用式6,来计算梯度 ∂ E d ∂ ω j i \frac{\partial E_d}{\partial \omega_{ji}} ∂ωji∂Ed的值,然后同我们神经网络代码中计算出来的梯度值进行比较。如果两者的差别非常的小,那么就说明我们的代码是正确的。
总结来看,如果我们想检查参数 ω j i \omega_{ji} ωji的梯度是否正确,我们需要以下几个步骤:
- 首先使用一个样本 d d d对神经网络进行训练,这样就能获得每个权重的梯度。
- 将 ω j i \omega_{ji} ωji加上一个很小的值( 1 0 − 4 10^{-4} 10−4),重新计算神经网络在这个样本下的 E d + E_{d+} Ed+。
- 将 ω j i \omega_{ji} ωji减上一个很小的值( 1 0 − 4 10^{-4} 10−4),重新计算神经网络在这个样本下的 E d − E_{d-} Ed−。
- 根据式6计算出期望的梯度值,和第一步获得的梯度值进行比较,它们应该几乎想等(至少4位有效数字相同)。
当然,我们可以重复上面的过程,对每个权重都进行检查。也可以使用多个样本重复检查。